Question

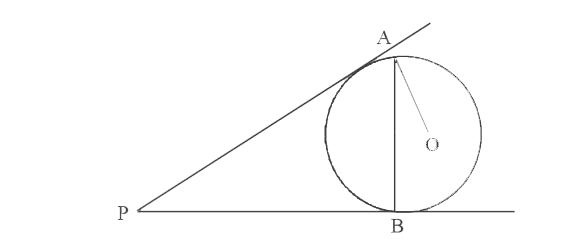
Two tangents PA and PB are drawn from an external point P to a circle with centre O at the point A and B respectively on it, such that $\angle APB={120}^{\circ }$, and AP= 12.5 cm. The length of OP is:
दो स्पर्शरेखाएँ PA और PB एक बाहरी बिंदु P से एक बिंदु पर क्रमशः
केंद्र A और B पर O के साथ वृत्त की ओर खींची जाती हैं, जैसे कि $\angle APB={120}^{\circ }$ और AP = 12.5 cm OP की लंबाई है:

Options

A. 24 cm
B. 25 cm
C. 26 cm
D. 20 cm

Explanation

To find the length of OP in the given problem, we will use the properties of triangles and the special ratios of a 30-60-90 triangle.

1. Identify the Given Information:
- The tangents PA and PB are drawn from point P to the circle at points A and B.
- The angle ∠APB = 120°.
- The length of PA = 12.5 cm.

2. Determine the Angles:
- Since PA and PB are tangents to the circle, the angles ∠PAO and ∠PBO are both 90° (tangent to radius).
- Therefore, triangle OAP and OBP are right triangles.
- The angle ∠APB can be split into two equal angles: ∠APO and ∠BPO. Thus, ∠APO = ∠BPO = 60° (since 120°/2 = 60°).

3. Analyze Triangle OAP:
- In triangle OAP, we have:
- ∠PAO = 90° (tangent property)
- ∠APO = 60°
- Therefore, ∠OAP = 30° (since the angles in a triangle sum to 180°).

4. Use the 30-60-90 Triangle Ratios:
- In a 30-60-90 triangle, the ratios of the sides opposite the angles are:
- Opposite 30°: 1 unit
- Opposite 60°: √3 units
- Opposite 90°: 2 units
- Here, PA (which is opposite the 60° angle) corresponds to 12.5 cm.

5. Calculate the Length of OP:
- Since PA corresponds to √3 units, we can set up the ratio:
- If √3 units = 12.5 cm, then 1 unit = 12.5/√3 cm.
- The length of OP corresponds to 2 units:
- OP = 2 * (12.5/√3) cm.
- To find OP, we can also use the property of the triangle:
- OP = 12.5 * 2 = 25 cm (since OP corresponds to the side opposite the 90° angle).

6. Final Answer:
- The length of OP is 25 cm.