In △PQR, the side QR is
extended to S such that RS = PR.
If ∠QPS=110∘ and ∠PRQ=70∘, then the value of ∠PQR is:
PQR में, भुजा QR को S तक बढ़ाया जाता है ऐसा कि RS = PR. यदि ∠QPS=110∘ और ∠PRQ=70∘, तो ∠PQR का मान है:
50∘
40∘
35∘
45∘
To find the value of angle PQR in triangle PQR, let's follow these steps:
Step 1: Understand the Geometry
We have triangle PQR, where the side QR is extended to point S such that RS = PR. We are given:
- Angle QPS = 110°
- Angle PRQ = 70°
Step 2: Identify Angles
Since RS = PR, triangle PRS is isosceles. Therefore, the angles opposite the equal sides (PR and RS) are equal. Let's denote these angles as x. So, we have:
- Angle PRS = x
- Angle RSP = x
Step 3: Use the Exterior Angle Theorem
The exterior angle theorem states that the exterior angle (angle QPS) is equal to the sum of the two opposite interior angles (angles PRS and PRQ). Therefore, we can write:
Angle QPS=Angle PRS+Angle PRQ
Substituting the known values:
110°=x+70°
Step 4: Solve for x
Now, we can solve for x:
x=110°−70°
x=40°
Step 5: Find Angle PQR
Now we know that angle PRS = 40°. Since triangle PQR's angles must sum to 180°, we can write:
Angle PQR+Angle QPR+Angle PRQ=180°
Substituting the known values:
Angle PQR+40°+70°=180°
Angle PQR+110°=180°
Step 6: Solve for Angle PQR
Now, we can isolate angle PQR:
Angle PQR=180°−110°
Angle PQR=70°
Final Answer
Thus, the value of angle PQR is:
Angle PQR=70°
---
We have triangle PQR, where the side QR is extended to point S such that RS = PR. We are given:
- Angle QPS = 110°
- Angle PRQ = 70°
Since RS = PR, triangle PRS is isosceles. Therefore, the angles opposite the equal sides (PR and RS) are equal. Let's denote these angles as x. So, we have:
- Angle PRS = x
- Angle RSP = x
The exterior angle theorem states that the exterior angle (angle QPS) is equal to the sum of the two opposite interior angles (angles PRS and PRQ). Therefore, we can write:
Angle QPS=Angle PRS+Angle PRQ
Substituting the known values:
110°=x+70°
Now, we can solve for x:
x=110°−70°
x=40°
Now we know that angle PRS = 40°. Since triangle PQR's angles must sum to 180°, we can write:
Angle PQR+Angle QPR+Angle PRQ=180°
Substituting the known values:
Angle PQR+40°+70°=180°
Angle PQR+110°=180°
Now, we can isolate angle PQR:
Angle PQR=180°−110°
Angle PQR=70°
Thus, the value of angle PQR is:
Angle PQR=70°
Topper's Solved these Questions
Similar Questions
Knowledge Check
PQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?
 A45B50C55D41
A45B50C55D41In △ PQR, PQ = PR, QR is extended to S and ∠PRS=110∘. Then, ∠PQR = .........
A30∘B50∘C80∘D70∘The side QR of ΔPQR is produced to S. If ∠PRS=105∘ and ∠Q=(12)∠P, then what is the value of ∠P ?
A45B60C70D75
In △PQR,∠Q≻∠R, PS is the bisector of ∠P and PT⊥QR. If ∠SPT=28∘ and ∠R=23∘ , then the measure of ∠Q is:
त्रिभुज PQR में, ∠Q≻∠R, है तथा PS कोण P का समद्विभाजक है और PT⊥QR है । यदि ∠SPT=28∘ और ∠R=23∘ है, तो कोण Q का मान क्या है?
View SolutionIn △PQR, QT is perpendicular to PR and s is a point on QR such that, ∠PSQ=p∘. If ∠TQR=46∘ and ∠SPR=32∘, then the value of p is :
त्रिभुज PQR में, QT, PR पर लंब है और QR पर बिंदु s इस प्रकार पर है कि ∠PSQ=p∘ है| यदि ∠TQR=46∘ और ∠SPR=32∘ है, तो p का मान ज्ञात करें|
View SolutionPQR is a triangle in which PR=QR. Side PR is extended to S, such that QR=RS. If ∠QPR=40∘, then what is the value (in degrees) of ∠QSR?

View SolutionIn a ∠PQR, M lies on PR and between P and R such that QR=QM=PM. If ∠MQR=40∘, then find ∠P.
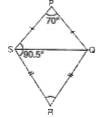
View SolutionPQRS is a kite. ∠P=70∘,∠S=90.5∘,∠R equals
View Solution
