In a △ABC,∠A=90∘, if
BM and CN are two medians, BM2+CN2BC2 is equal to:
△ABC में, ∠A=90∘, अगर BM और CN दो मध्यिका हैं, तो BM2+CN2BC2 बराबर है:
3/5
4/5
5/4
3/4
To solve the problem, we need to find the value of (BM2+CN2)/(BC2) in triangle ABC where ∠A=90∘ and BM and CN are the medians from vertices B and C respectively.
1. Identify the Triangle and Medians:
- Given triangle ABC with ∠A=90∘.
- Let AB=c, AC=b, and BC=a.
2. Calculate the Length of the Medians:
- The formula for the length of a median from vertex B to side AC (median BM) is given by:
BM=12√2AB2+2AC2−BC2
Substituting the sides:
BM=12√2c2+2b2−a2
- The formula for the length of the median from vertex C to side AB (median CN) is:
CN=12√2AC2+2AB2−BC2
Substituting the sides:
CN=12√2b2+2c2−a2
3. Calculate BM2 and CN2:
- Squaring the medians:
BM2=(12√2c2+2b2−a2)2=14(2c2+2b2−a2)
CN2=(12√2b2+2c2−a2)2=14(2b2+2c2−a2)
4. Add BM2 and CN2:
- Adding the two squared medians:
BM2+CN2=14(2c2+2b2−a2)+14(2b2+2c2−a2)
=14(4b2+4c2−2a2)=14(4(b2+c2)−2a2)
Since in a right triangle, a2=b2+c2:
=14(4(b2+c2)−2(b2+c2))=14(2(b2+c2))=12(b2+c2)
5. Calculate BC2:
- Since BC=a, we have:
BC2=a2=b2+c2
6. Final Calculation:
- Now substituting back into the expression:
BM2+CN2BC2=12(b2+c2)b2+c2=12
Conclusion:
Thus, the value of BM2+CN2BC2 is 12.
- Given triangle ABC with ∠A=90∘.
- Let AB=c, AC=b, and BC=a.
- The formula for the length of a median from vertex B to side AC (median BM) is given by:
BM=12√2AB2+2AC2−BC2
Substituting the sides:
BM=12√2c2+2b2−a2
- The formula for the length of the median from vertex C to side AB (median CN) is:
CN=12√2AC2+2AB2−BC2
Substituting the sides:
CN=12√2b2+2c2−a2
- Squaring the medians:
BM2=(12√2c2+2b2−a2)2=14(2c2+2b2−a2)
CN2=(12√2b2+2c2−a2)2=14(2b2+2c2−a2)
- Adding the two squared medians:
BM2+CN2=14(2c2+2b2−a2)+14(2b2+2c2−a2)
=14(4b2+4c2−2a2)=14(4(b2+c2)−2a2)
Since in a right triangle, a2=b2+c2:
=14(4(b2+c2)−2(b2+c2))=14(2(b2+c2))=12(b2+c2)
- Since BC=a, we have:
BC2=a2=b2+c2
- Now substituting back into the expression:
BM2+CN2BC2=12(b2+c2)b2+c2=12
Thus, the value of BM2+CN2BC2 is 12.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If ABC is a right angled triangle at B and M, N are the mid-points of AB and BC, then 4(AN2+CM2) is equal to :
A4AC2B6AC2C5AC2D54AC2In a triangle ABC if ∠ABC=60∘, then (AB−BC+CAr)2=
A10B11C12D14
In △ABC, ∠C=90∘, Points P and Q are on the sides AC and BC, respectively, such that AP :PC =BQ: QC=1:2 Then AQ2+BP2AB2 is equal to:
△ABC में ∠C=90∘, बिंदु P और Q क्रमशः AC और BC पर बिंदु इस प्रकार है की AP :PC =BQ: QC=1:2 तो AQ2+BP2AB2 = ?
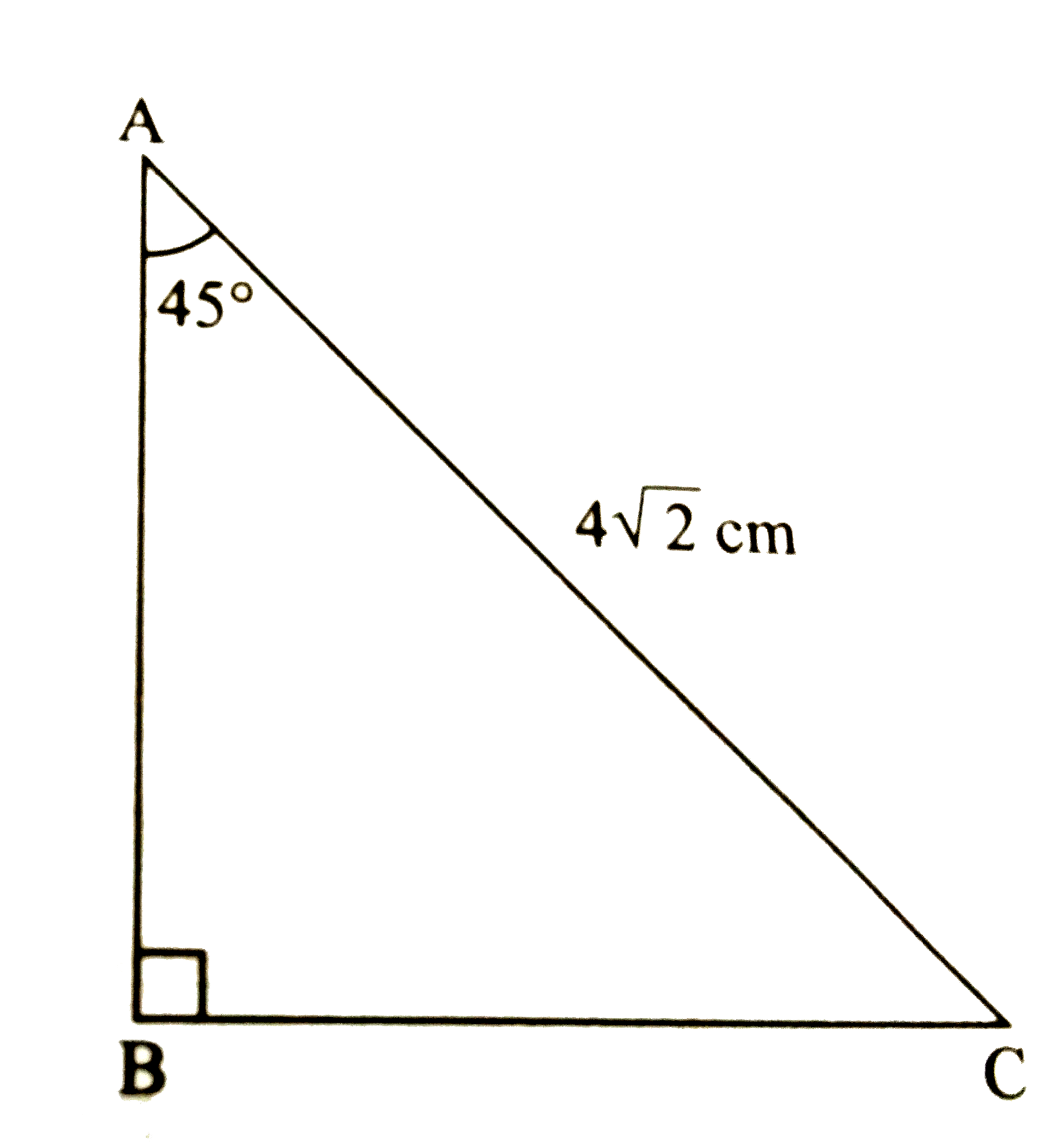
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn the triangle ABC, D is on BC ∠ADB=90∘,∠ABC=45∘, AD= 10cm, AC = 20 cm. then BC is equal to:
View SolutionIn a △ABC, ∠BAC=90∘ and AD is perpendicular to BC where D is a point on BC. If BD = 4 cm and CD = 5cm then the length of AD is equal to:
△ABC में, ∠BAC=90∘ और AD, BC पर लंबवत है जहाँ D, BC पर एक बिंदु है। यदि BD =4 सेमी और CD =5 सेमी तो AD की लंबाई ज्ञात करे
View SolutionIn △ABC ,∠A=90∘. M is the midpoint of BC and D is a point on BC such that AD⊥BC. If AB= 7 cm and AC = 24 cm, then AD:AM is equal to:
△ABC में, ∠A=90∘ है, M, BC का मध्य बिंदु है तथा D, BC पर स्थित ऐसा बिंदु है कि AD⊥BC है | यदि AB= 7 सेमी, AC = 24 सेमी है, तो AD:AM किसके बराबर है ?
View SolutionIn a triangle ABC,B=90∘ and D is the mid-point of BC then prove that AC2=AD2+3CD2
View Solution
