In △ABC,∠ABC=6∠ACB and ∠BAC=5∠ACB. If AB = 7 cm, and AC = 25 cm then the length of BC is equal to:
△ABC में, ∠ABC=6∠ACB और ∠BAC=5∠ACB। यदि AB = 7 सेमी, और AC =25 सेमी है, तो BC की लंबाई ज्ञात करे
24 cm
32 cm
26 cm
12 cm
To find the length of side BC in triangle ABC, we will use the given angle relationships and the Law of Sines.
1. Define the Angles:
Let the angle ACB be represented as x.
- Then, angle ABC = 6x
- And angle BAC = 5x
2. Use the Triangle Angle Sum Property:
According to the triangle angle sum property, the sum of the angles in a triangle is 180 degrees.
Angle A+Angle B+Angle C=180∘
Substituting the angles we defined:
5x+6x+x=180∘
Simplifying this gives:
12x=180∘
Therefore:
x=180∘12=15∘
3. Calculate Each Angle:
Now we can find the measures of each angle:
- Angle ACB = x=15∘
- Angle ABC = 6x=90∘
- Angle BAC = 5x=75∘
4. Use the Law of Sines:
The Law of Sines states:
asinA=bsinB=csinC
Where:
- a=BC
- b=AC=25cm
- c=AB=7cm
- A=∠ACB=15∘
- B=∠BAC=75∘
- C=∠ABC=90∘
5. Set Up the Ratios:
Using the Law of Sines, we can set up the ratio for side BC:
BCsinA=ACsinB
Substituting the known values:
BCsin15∘=25sin75∘
6. Calculate BC:
Rearranging gives:
BC=25⋅sin15∘sin75∘
We know that sin75∘=sin(90∘−15∘)=cos15∘.
Thus:
BC=25⋅sin15∘cos15∘=25⋅tan15∘
Using the approximate value tan15∘≈0.2679:
BC≈25⋅0.2679≈6.6975cm
Final Answer:
The length of BC is approximately 6.7cm.
Let the angle ACB be represented as x.
- Then, angle ABC = 6x
- And angle BAC = 5x
According to the triangle angle sum property, the sum of the angles in a triangle is 180 degrees.
Angle A+Angle B+Angle C=180∘
Substituting the angles we defined:
5x+6x+x=180∘
Simplifying this gives:
12x=180∘
Therefore:
x=180∘12=15∘
Now we can find the measures of each angle:
- Angle ACB = x=15∘
- Angle ABC = 6x=90∘
- Angle BAC = 5x=75∘
The Law of Sines states:
asinA=bsinB=csinC
Where:
- a=BC
- b=AC=25cm
- c=AB=7cm
- A=∠ACB=15∘
- B=∠BAC=75∘
- C=∠ABC=90∘
Using the Law of Sines, we can set up the ratio for side BC:
BCsinA=ACsinB
Substituting the known values:
BCsin15∘=25sin75∘
Rearranging gives:
BC=25⋅sin15∘sin75∘
We know that sin75∘=sin(90∘−15∘)=cos15∘.
Thus:
BC=25⋅sin15∘cos15∘=25⋅tan15∘
Using the approximate value tan15∘≈0.2679:
BC≈25⋅0.2679≈6.6975cm
The length of BC is approximately 6.7cm.
Topper's Solved these Questions
Similar Questions
In a △ABC, 2∠ABC=9∠ACB and 2∠BAC=7∠ACB. If AB = 8 cm, AC = 17 cm, then the length of BC is:
△ABC में, 2∠ABC=9∠ACB और 2∠BAC=7∠ACB| यदि AB =8 सेमी, AC =17 सेमी है, तो BC की लंबाई है:
View SolutionIn a right-angled triangle ABC, if angle B=90°, BC = 3 cm and AC = 5 cm, then the length of side AB is
View Solution
Knowledge Check
△ABC is right-angled at A. If AB = 24 cm and AC = 7 cm, then BC = ?
A31 cmB17 cmC25 cmD28 cmΔABC is right-angled at C. If AC=5cmandBC=12cm find the length of AB.
A17B7C13D14
Ina △ABC,∠BAC>90∘, then ∠ABC and ∠ACB must be :
View SolutionIn a △ABC, ∠BAC=90∘ and AD is perpendicular to BC where D is a point on BC. If BD = 4 cm and CD = 5cm then the length of AD is equal to:
△ABC में, ∠BAC=90∘ और AD, BC पर लंबवत है जहाँ D, BC पर एक बिंदु है। यदि BD =4 सेमी और CD =5 सेमी तो AD की लंबाई ज्ञात करे
View SolutionThe bisector of ∠B in △ABC meets AC at D. If AB = 10 cm, BC= 11 cm and AC = 14 cm, then the length of AD is:
△ABC में ∠B का समद्विभाजक AC से D पर मिलता है | यदि AB =10 सेमी, BC = 11 सेमी और AC =14 सेमी है, तो AD की लंबाई क्या होगी ?
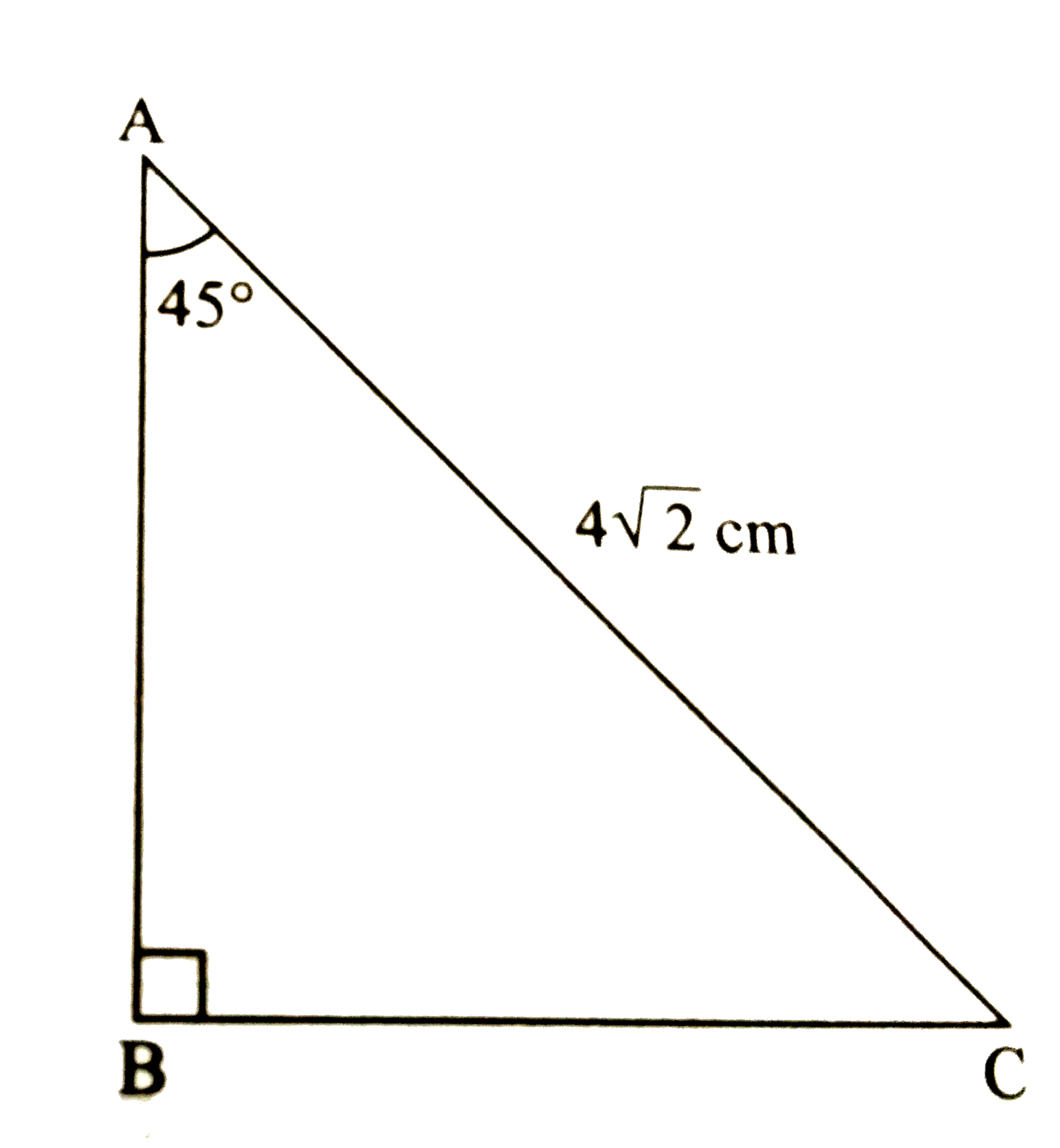
View SolutionIn △ABC,∠ABC=90∘
∠BAC=45∘ and AC =4√2cm,
then find AB.
View SolutionIn a triangle aBC ,∠B=2∠C.AD and BE bisectors of ∠BACand∠ABC. If AB=CD . Find ∠BAC
View SolutionIn △ABC ,D is a point on side BC such that ∠ADC=∠BAC. If CA = 12 cm, and CB = 8cm, then CD is equal to :
त्रिभुज ABC में, D भुजा BC पर स्थित एक बिंदु है जो इस प्रकार है कि ∠ADC=∠BAC है |यदि CA = 12 सेमी और CB = 8 सेमी है, तो CD का मान किसके बराबर होगा ?
View Solution
