Three particles A,B and C are situated at the vertices of an equilateral triangle of side l. Each of the particle starts moving with a constant velocity v such that A is always directed towards B,B towards C and C towards A. Find the time when they meet.
None
The correct Answer is:C
Relative velocity of apparoach
Distance between A and B =l

Similar Questions
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View SolutionThree particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
View Solution
Knowledge Check
Three particles A, B and C are situated at the vertices of an equilateral triangle ABC of side d at time t=0. Each of the particles moves with constant speed v. A always has its velocity along AB, B along BC and C along CA. At what time will the particles meet each other?
At=dvBt=3d2vCt=2d3vDt=0Three particles A,B and C and situated at the vertices of an equilateral triangle ABC of side of length l at time t=0,Each of the particles move with constant speed u. A always has its velocity along AB,B along BC and C along CA.
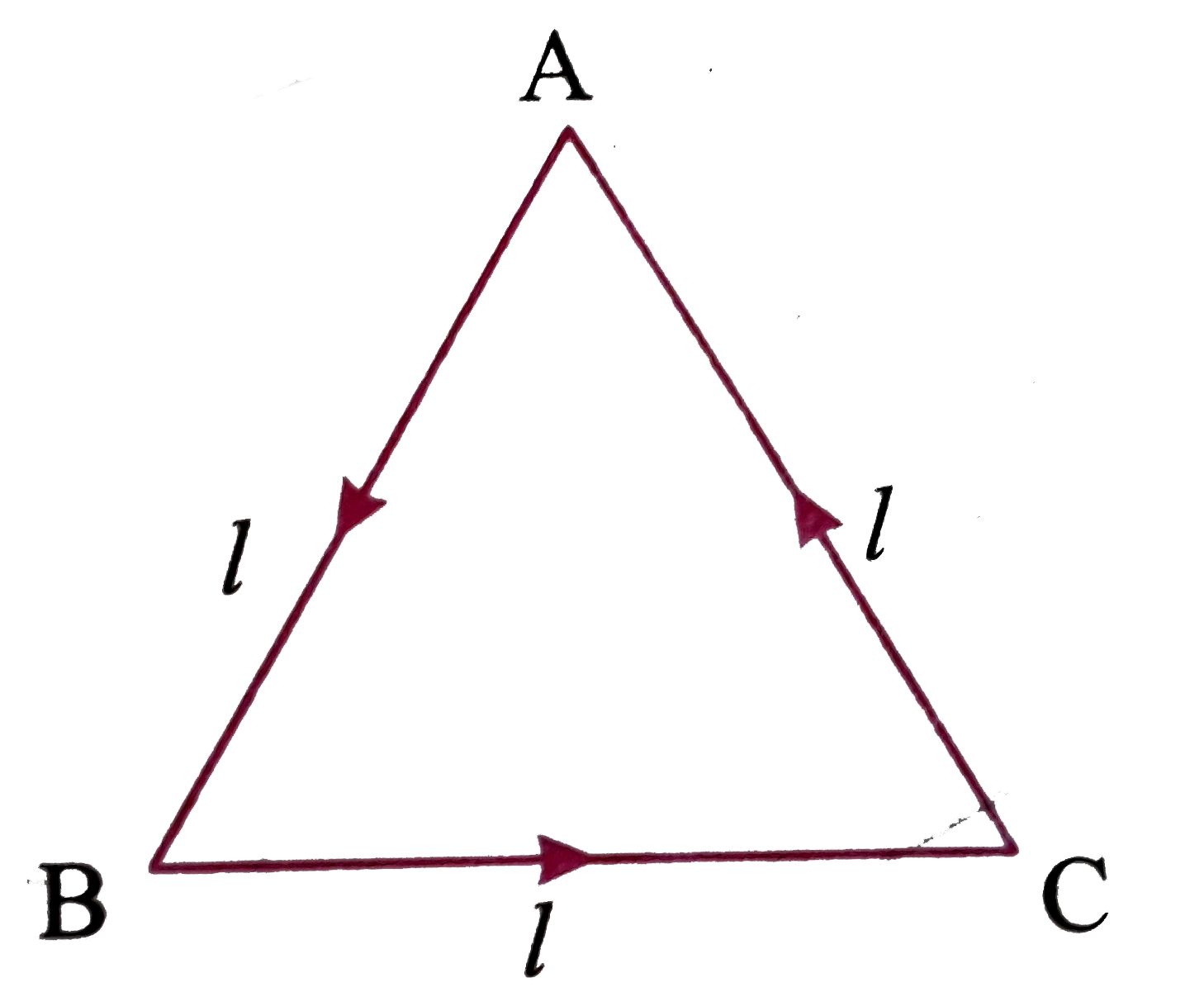 AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2
AThe time after which they meet is 2l3uBTotal distance travelled by each particle before they meet is 2l3CAverage velocity during the motion is √3u2DRelative velocity of apporach between any two particles is 3u2Three particles A,B and C situated at vertices of an equilateral triangle, all moving with same constant speed such that A always move towards B,B always towards C and C always towards A. Initial seperation between each of the particle is a. O is the centroid of the triangle. Distance covered by particle A when it completes one revolution around O is
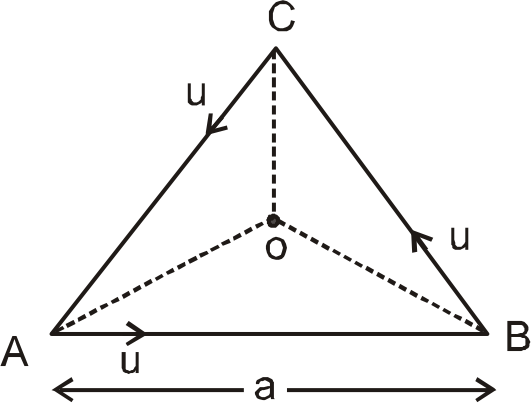 A2a(1−e−2√3π)B2a3(1−e−2√3π)Ca(1+e−2√3π)D2a3(1−e−√3π)
A2a(1−e−2√3π)B2a3(1−e−2√3π)Ca(1+e−2√3π)D2a3(1−e−√3π)
Three boys A,B and C are situated at the vertices of an equilateral triangle of side d at t=0. Each of the boys moves with constant speed v. A always moves towards C and C towards A, At what time and where they meet each other?
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of
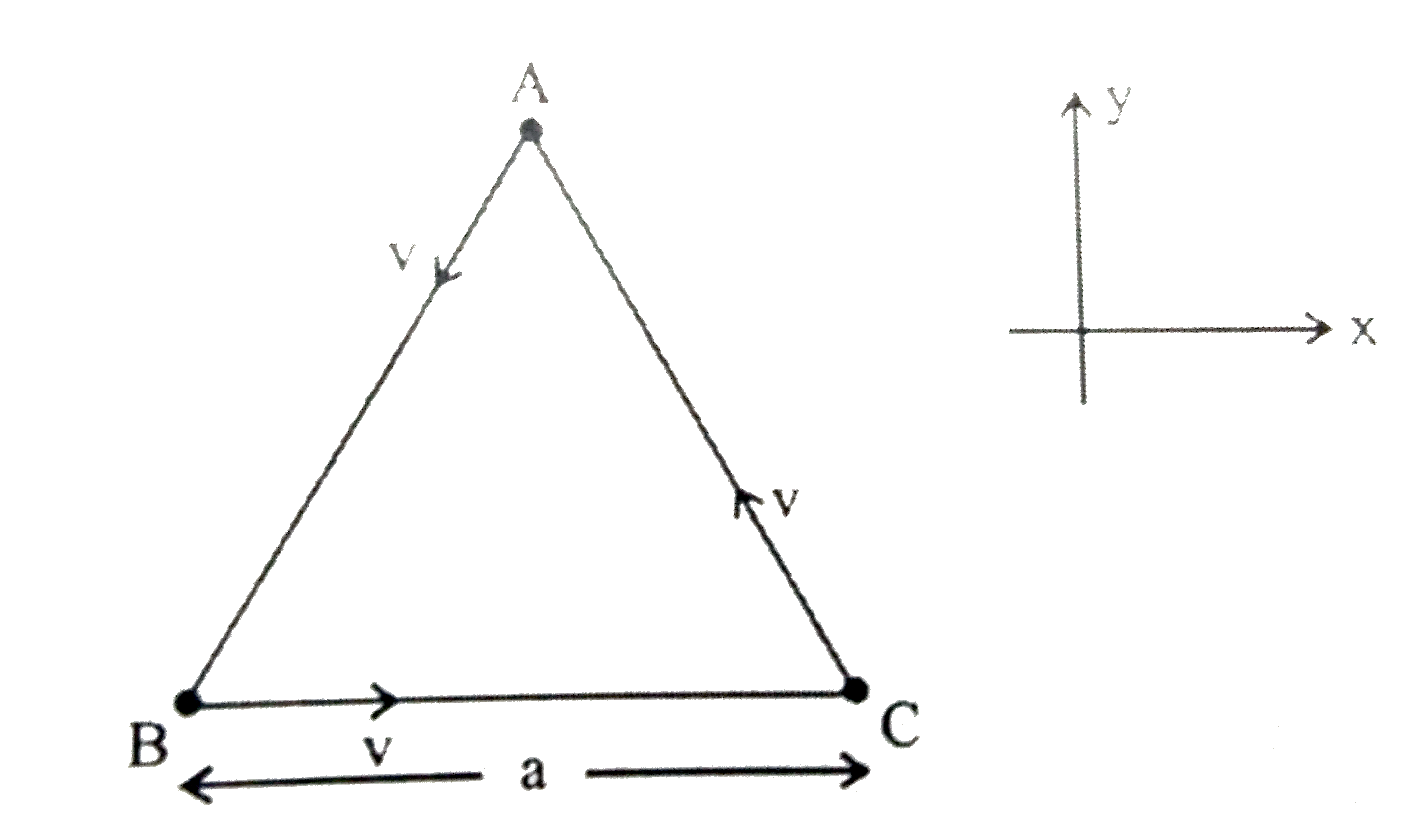
View SolutionThree particles of equal mass 'm' are situated at the vertices of an equilateral triangle of side L. The work done in increasing the side of the triangle to 2L is
View SolutionThree particles A, B, Care located at the comers of an equilateral triangle as shown in figure. Each of the particle is moving with velocity v. Then at the instant shown, the relative angular velocity of

View Solution
