A ball collides elastically with another ball of the same mass. The collision is oblique and initially one of the balls was at rest. After the collision, the two balls move with same speeds. What will be the angle between the velocity of the ball after the collision?
30∘
45∘
60∘
90∘
The correct Answer is:B
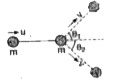
Applying law of conservation of momentum along horizontal and vertical directions, we get,
mvsinθ1−mvsinθ2=0
i.e., θ1=θ2 ...(1)
Also , mu=mv(cosθ1+cosθ2)=2mvcosθ[θ1=θ2=θ(say)]
cosθ=u2v .....(2)
According to law conservation of kinetic KE, 12mu2=12mv2+12mv2
or u2=2v2 or u=√2v ....(3)
From eqn. (2) and eqn. (3), cosθ=√2v2v or ,cosθ=1√2 or θ=45∘
Hence θ1=θ2=45∘
Similar Questions
A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,

View SolutionA smooth ball 'A' moving with velocity 'V' collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities 60∘. No external force acts on the system of balls.

The speed of each ball after the collision is
View Solution
Knowledge Check
A ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
A30∘B60∘C120∘D90∘A ball A of mass M collides elastically with a similar ball B at rest as shown in figure. Initially velocity of ball A is u m/s. After collision,
 ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatj
ASpeed of ball B is u sinθBVelocity of ball A is usin2θˆi+usinθcosθˆjCSpeed of ball A is ucosθDVelocityofballBisu cos theta sin theta hati + u cos^2 theta hatjA smooth ball 'A' moving with velocity 'V' collides with another smooth identical ball at rest. After collision both the balls move with same speed with angle between their velocities 60∘. No external force acts on the system of balls.

The speed of each ball after the collision isAv2Bv3CV√3D2V√3
Two balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View SolutionA ball of mass 5 kg travelling with velocity of 15 cm/s makes a head on collision with another ball of mass 1 kg which is at rest. After the collision, the speed of the lighter ball is
View SolutionTwo balls each of mass 2kg (one at rest) undergo oblique collision is perfectly elastic, then the angle between their velocities after collision is
View SolutionTwo balls of equal masses m each undergo oblique collision. If colision is perfectly elastic, then angle between their velocities after collision is
View Solution
