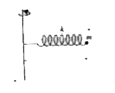
A particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l . The system is rotated about the other end of the spring with an angular velocity w, in gravity-free space. The increase in length of spring will be
mω2lk+mω2
mω2lk−mω2
mω2lk+mω
mω2lk−mω
The correct Answer is:B
Let the spring increase by x. Force=kx.
Radius of circle =(l+x) ∴ Centripetal force=Force due to spring
or mRω2=kx or m(l+x)ω2=kx
or mlω2=kx−mxω2=x(k−mω2) or x=mω2l(k−mω2)
Similar Questions
A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is

View SolutionA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
View Solution
Knowledge Check
A particles of mass m is fixed to one end of a light spring of force constant k and unstreatched length l. the system is rotated about the other end of the spring with an angular velocity ω in gravity free space. The increase in length of the spring is
 Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2Dnone of theseA particle of mass m is fixed to one end of a massless spring of spring constant k and natural length l0. The system is rotated about the other end of the spring with an angular velocity ω ub gravity-free space. The final length of spring is
Amω2l0kBmω2l0k−mω2Ckl0k−mω2Dmω2l0k+mω2A particle of mass m is fixed to one end of a light spring of force constant k and unstretched length l. The other end of the spring is fixed on a vertical axis which is rotaing with an angular velocity ω. The increase in length of th espring will be
 Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
Amω2lkBmω2lk−mω2Cmω2lk+mω2DNone of these
A block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA light rod AB is fitted with a small sleeve of mass m which can slide smoothly over it. The sleeve is connected to the two ends of the rod using two springs of force constant 2k and k (see fig). The ends of the springs at A and B are fixed and the other ends (connected to sleeve) can move along with the sleeve. The natural length of spring connected to A is l0. Now the rod is rotated with angular velocity w about an axis passing through end A that is perpendicular to the rod. Take kmω2=η and express the change in length of each spring (in equilibrium position of the sleeve relative to the rod) in terms of l0 and η.

View SolutionA block of mass m is connected at one end of spring fixed at other end having natural length l0 and spring constant K. The block is rotated with constant angular speed (ω) in gravity free space. Find the elongation in spring.
View SolutionA spring of force constant K rests on a smooth floor, with one end fixed to a wall. A block of mass m hits the free end of the spring with velocity v. The maximum force exerted by the spring on the wall is
View SolutionA ball of mass m is attached to the lower end of a light vertical spring of force constant K. The upper end of the spring is fixed. The ball is released from rest with the spring at its normal ( unstretched ) length, and comed to rest again after descending through a distance x.
View Solution
