A concave mirror of radius of curvature 60cm is placed at the bottom of a tank filled with water upto a height of 20cm. The mirror faces upwards with its axis vertical. Solar light falls vertically (normally) on the surface of then with the observer in air, the distance of the image from water and the image of the sun is formed. If the surface of water is
30 cm
10 cm
7.5 cm above
7.5 cm
The correct Answer is:C
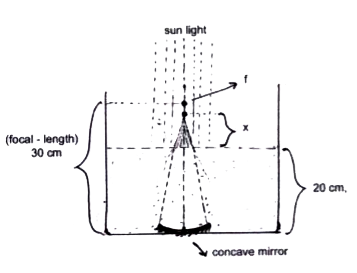
Given
Thus, the image would have been formed at f. (f is 10 cm above the water surface)
But due to refraction at water-air interface, the image forms below the point f.
Given,
Taken .x. as the apparent - height,
Thus, image forms at the point, 7.5 cm above the water-surface.
Similar Questions
A concave mirror of radius of curvature 60 cm is placed at the bottom of tank containing water upto a height of 20 cm. The mirror faces upwards with its axis vertical. Solar light falls normally on the surface of water and the image of the sun is formed. If aμw=43 then with the observer in air, the distance of the image from the surface of water is:
View SolutionA concave mirror of radius of curvature one meter is placed at the bottom of a tank of water. The mirror forms an image of the sun when it is directly overhead. Calculate the distance of the images from the mirror for (a) 80cm and (b) 40cm of water in the tank ( μ=4/3 for water)
View Solution
Knowledge Check
- Question 1 - Select One
A concave mirror of radius of curvature 60 cm is placed at the bottom of tank containing water upto a height of 20 cm. The mirror faces upwards with its axis vertical. Solar light falls normally on the surface of water and the image of the sun is formed. If aμw=43 then with the observer in air, the distance of the image from the surface of water is:
A30 cmB10 cmC7.5 cm aboveD7.5 cm below - Question 2 - Select One
A concave mirror is placed at the bottom of an empty tank with face upwards and axis vertical. When sunlight falls normally on the mirror, it is focussed at distance of 32cm from the mirror. If the tank filled with water (μ=4/3) up to a height of 20cm, then the sunlight will now get focussed at
A16cm above water levelB9cm above water levelC24cm below water levelD9cm below water level - Question 3 - Select One
A concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
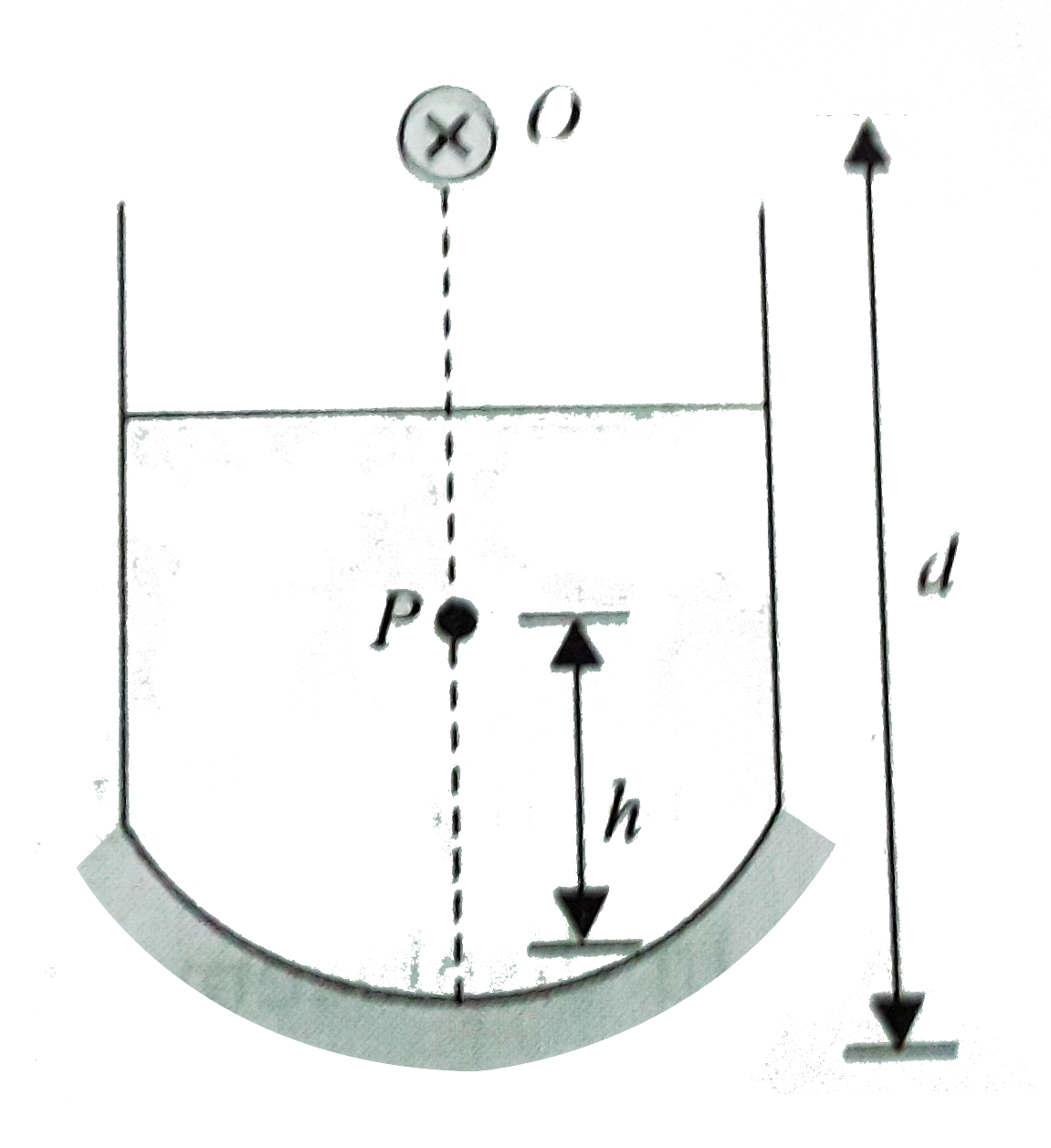Ah(1−1μ)B2hμ−1CzeroD2hμ
A concave mirror is placed at the bottom of an empty tank with face upwards and axis vertical. When sunlight falls normally on the mirror, it is focussed at distance of 32cm from the mirror. If the tank filled with water (μ=4/3) up to a height of 20cm, then the sunlight will now get focussed at
View SolutionA concave mirror of radius of curvature h is placed at the bottom of a tank containing a liquid of refractive index μ upto a depth d. An object P is placed at height h above the bottom of the miror. Outside the liquid, an observer O views the object and its image in the mirror. The apparent distance between these two will be
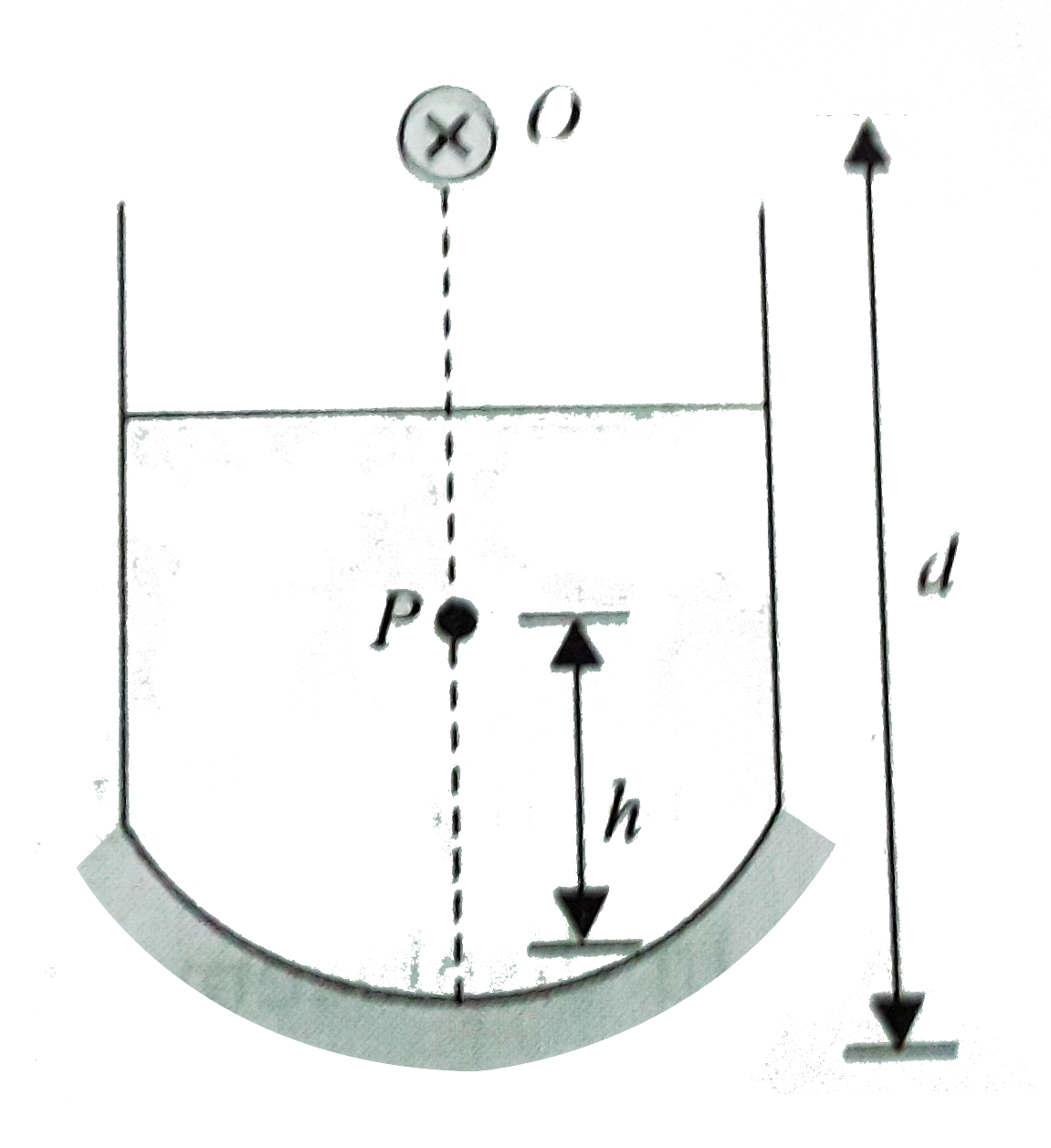View SolutionWater is filled in a container upto a height of 5cm. There is a concave mirror of radius of curvature 40cm. A person just above the surface observes image of 'A'. The distance of image from water surface is (μwater=1.33):
_2019_CBT7_E01_003_Q01.png)
View SolutionA plane mirror is fixed at the bottom of a tank containing water. A small object is kept at a height of 24 cm from the bottom and is viewed from a point vertically above it. The distance between the object and the image in the mirror as appears to the person is
View SolutionWater is filled in a container upto a height of 5cm. There is a concave mirror of radius of curvature 40cm. A person just above the surface observes image of 'A'. The distance of image from water surface is (μwater=1.33):
View Solution