Two particles of equal masses m and m are connected by a light string of length 2l. A constant force F is applied continuously at the mid-point of the string, always along the perpendicular bisector of the straight line joining the two particles. Show that when the distance between the two particles is x, the acceleration of the particle is
a=Fm=x(12−x2)1/2Solution in Punjabi
Step by step video & image solution for Two particles of equal masses m and m are connected by a light string of length 2l. A constant force F is applied continuously at the mid-point of the string, always along the perpendicular bisector of the straight line joining the two particles. Show that when the distance between the two particles is x, the acceleration of the particle is a = F/m = (x)/((1^2 - x^2) ^(1//2) by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Topper's Solved these Questions
Similar Questions
What is the difference between gravity and gravitation?
04:35View SolutionWhat is the unit of torr?
09:04View SolutionTwo particles are moving along x-axis. Particle-1 is 40 m behind Particle-2. Particle-1 starts with velocity 12 m//s and acceleration 4 m//s^2 both in positive x-direction. Particle-2 starts with velocity 4 m//s and acceleration 12 m//s^2 also in positive x-direction. Find (a) the time when distance between them is minimum. (b) the minimum distacne between them.
02:40View SolutionMass M is distributed uniformly along a line of length 2L. A particle of mass m is at a point that is at a distance a above the centre of the line on the its perpendicular bisector (Point P in figure). The gravitational force that the line exert on the particle is
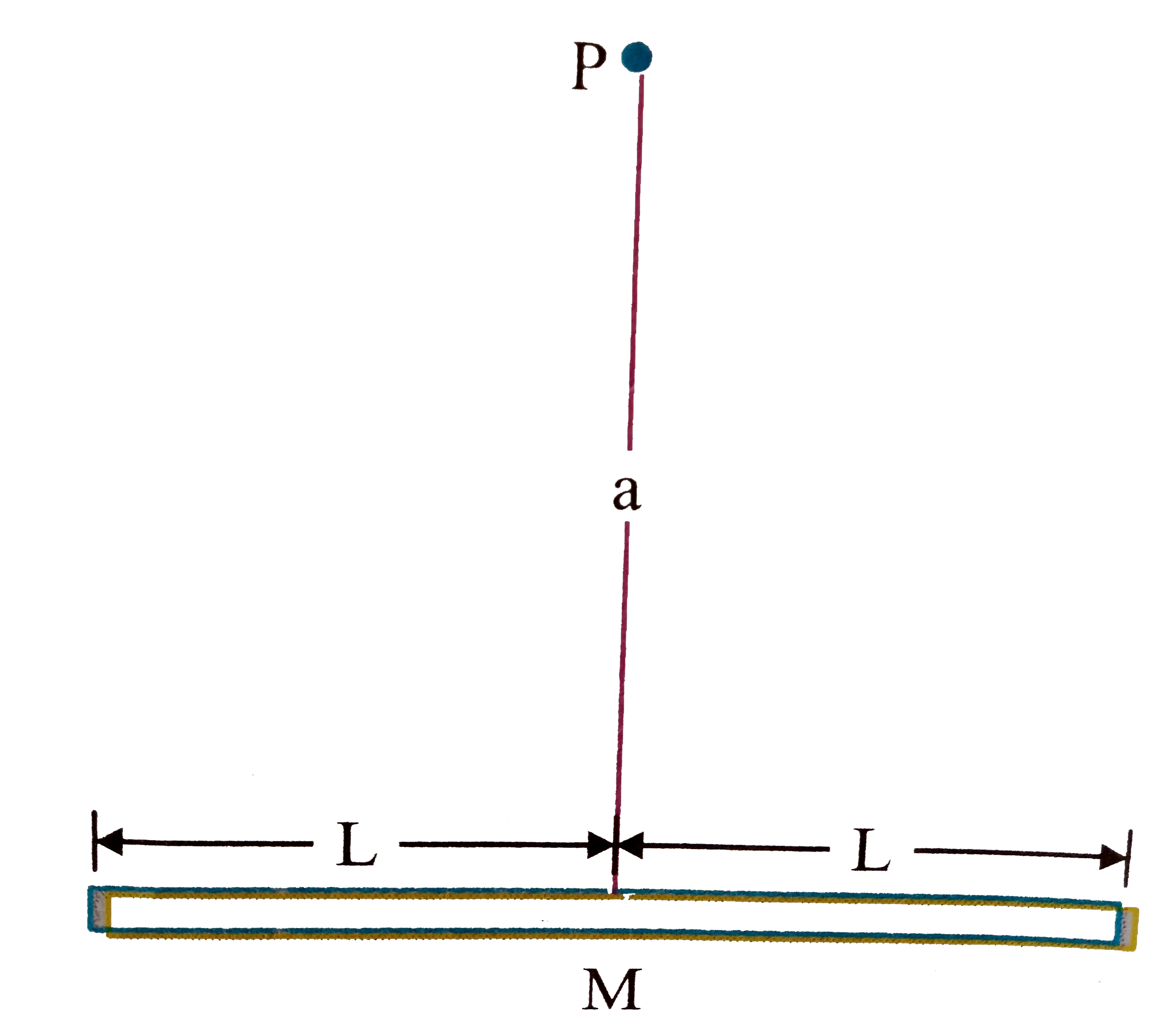 03:20View Solution
03:20View SolutionTwo particles each of mass m are connected by a light string of length 2L as shown in the figure. A constant force F is applied continuoulsly at the mid−point of the string at right−angle to intial position of the string. Find the acceleration of each particle and the acceleration of approach between the particles when separation between them is 2x
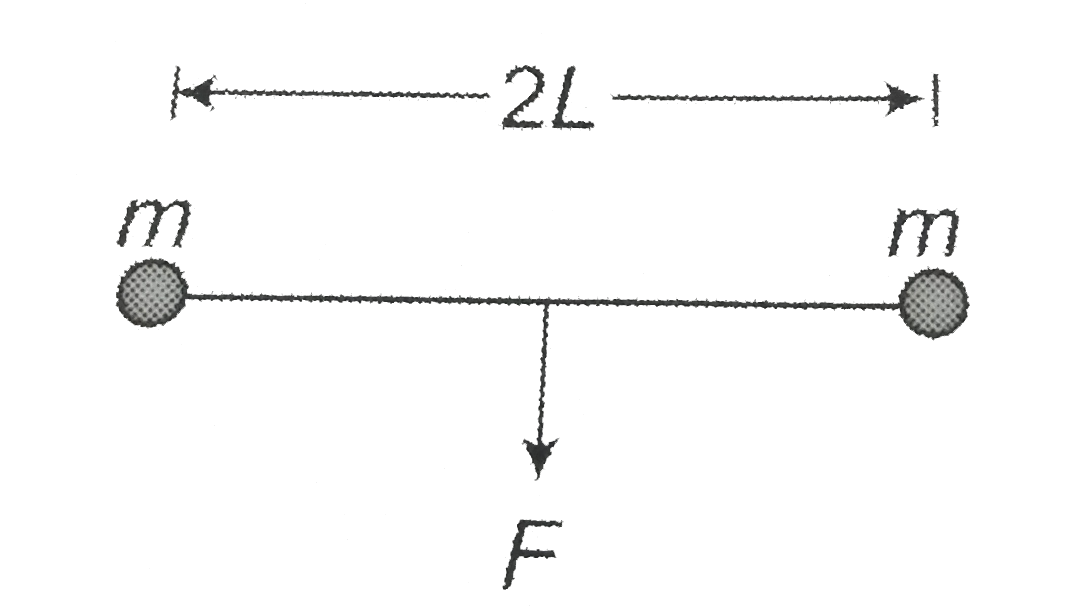 06:05View Solution
06:05View SolutionTwo particles each of mass m are connected by a light inextensible string and a particle of mass M is attached to the midpoint of the string. The system is at rest on a smooth horizontal table with string just taut and in a straight line. The particle M is given a velocity v along the table perpendicular to the string. Prove that when the two particles are about to collide :
(i) The velocity of M is Mv(M+2m)
(ii) The speed of each of the other particles is (√2M(M+m)(M+2m))v.04:18View SolutionTwo particles, each of mass m, are connected by a light string of length 2L as shown in A continuous force F is applied at the mid point of the string (x=0) at right angles to the initial position of the string. Show that acceleration of m in the direction at right angles to F is given by
ax=F2mx√L2−x2
where x is the perpendicular distance of one of the particles from the line of action of F. Discuss the situation when x=L05:06View SolutionTwo particles of masses m and M(Mgtm) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
07:34View Solutionदो कण जिनमें से प्रत्येक का द्रव्यमान m है 2a लम्बाई की एक हल्की डोरी के किनारों पर बंधे है। यह सम्पूर्ण निकाय एक घर्षणहीन क्षैतिज तल पर इस प्रकार रखा है की डोरी तनी हुई है तथा प्रत्येक कण डोरी के मध्य-बिंदु P से 'a ' दुरी पर है (जैसे की चित्र में दिखाया गया है)। अब डोरी के मध्य- बिंदु को ऊर्ध्वाधर दिशा में ऊपर की ओर एक लघु, किन्तु एकसमान परिमाण के बल F से खिंचा जाता है। परिणाम स्वरूप, कण क्षैतिज तल पर एक-दूसरे की ओर चलने लगते है। जब कणों के बीच दुरी 2x हो जाती है, तब उनके त्वरणों का परिणाम है:
 View Solution
View SolutionA light smooth inextensible string connected with two identical particles each or mass m, passes through a light ring R. If a force F pulls ring, the relative acceleration between the particles has magnitude : P
02:39View SolutionWhen forces F1,F2,F3 are acting on a particle of mass m such that F1 and F2 are mutually perpendicular, then the particle remains stationary, If the force F, is now removed then acceleration of the particle is
08:37View SolutionWhen forces F1,F2 and F3 are acting on a particle of mass m such that F2 and F3 are m utually perpendicular, then the particle remains stationary. If the force F x is now removed, then the acceleration of the particle is .........
03:46View SolutionA light smooth inextensible string connected with two identical particles each of mass m, passes through a light ring R. If a force F pulls ring, the relative acceleration between the particles has magnitude :
04:02View SolutionTwo particles are moving along x-axis. Particle-1 is 40 m behind Particle-2. Particle-1 starts with velocity 12 m//s and acceleration 4 m//s^2 both in positive x-direction. Particle-2 starts with velocity 4 m//s and acceleration 12 m//s^2 also in positive x-direction. Find (a) the time when distance between them is minimum. (b) the minimum distacne between them.
04:25View SolutionTwo particles of masses m and M(Mgtm) are connected by a cord that passes over a massless, frictionless pulley. The tension T in the string and the acceleration a of the particles is
04:22View Solution

