Consider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
Let PA=4 , PB=3 cm and CD is diameter of the circle having the length 8. If PC>PD , then PCPD is equal to Solution in Gujrati
3
4
5
6
The correct Answer is:A
Step by step video & image solution for Consider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) . On the basis of above information , answer the questions Let PA=4 , PB=3 cm and CD is diameter of the circle having the length 8. If PC gt PD , then (PC)/(PD) is equal to by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
In the given figure PA=6, PB=4 and PC=8. Find PD.

View Solutionदिये गये चित्र में (वृत्त) PT = 5. PD=7 तथा PA = 2 हो, तो PB – PC का मान ज्ञात कीजिए।
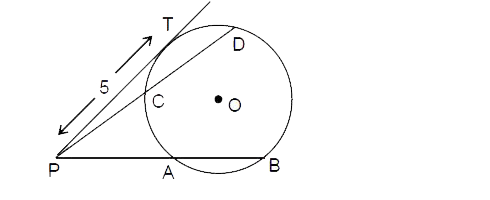
View SolutionIf chords AB and CD of a circle intersect each other at a point inside the circle, prove that : PA×PB=PC×PD .
View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If PA=|cosθ+sinθ|andPB=|cosθ−sinθ|, then maximum value of (PC)(PD) , is equal to
View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If logPAx=2,logPBx=3,logxPC=4, then logPD x is equal to
View SolutionIn the given figure, PA and PB are tangents to the circle from an external point P. CD is another tangent touching the circle at Q. If PA =12 cm, QC=3cm, then find PC+PD.
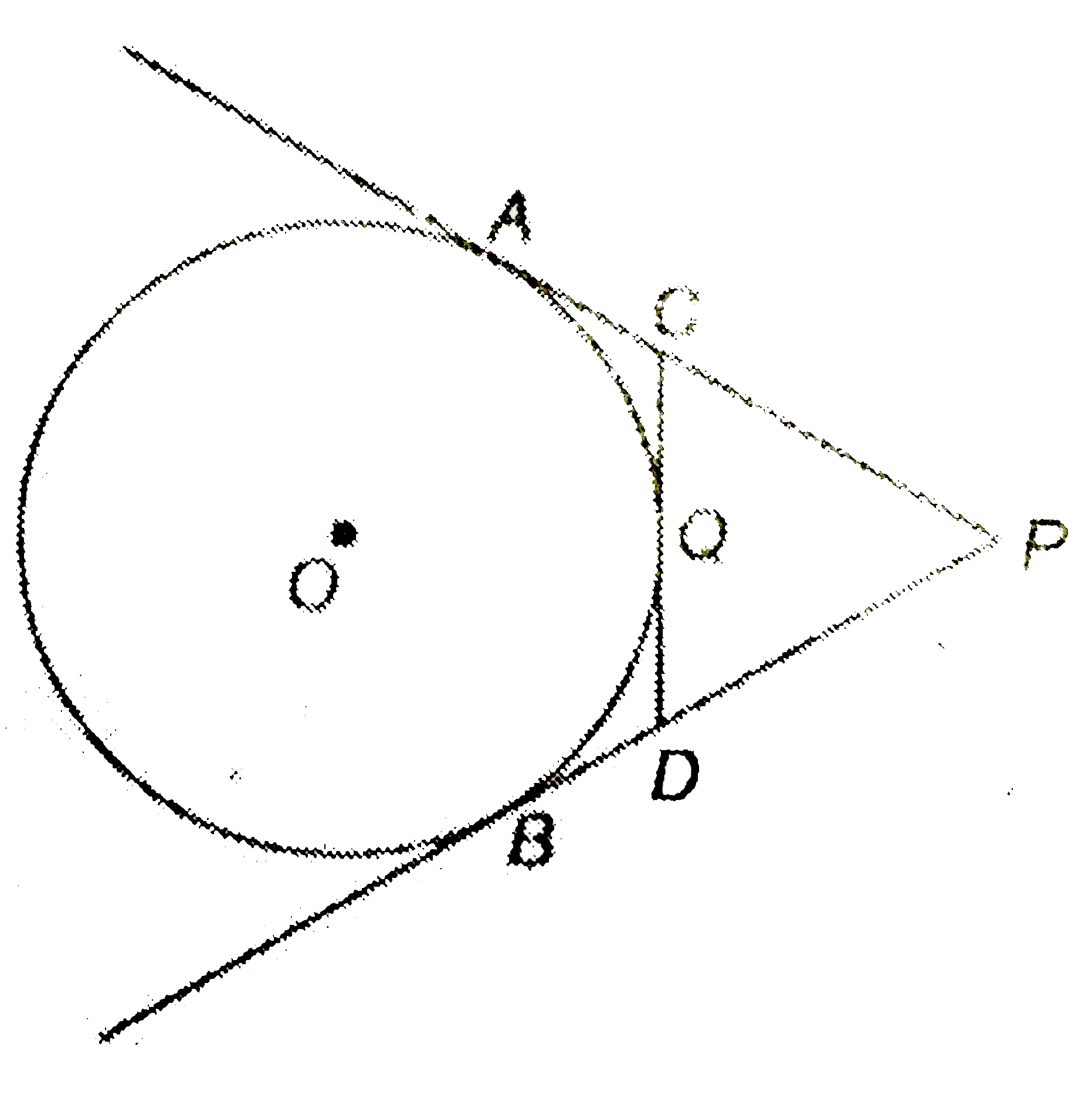
View SolutionIn the figure, the strings AB and CD of the circle are stretched and bent at point P. PA xx PB = PC xx PD Prove that.
View SolutionConsider a circle , in which a point P is lying inside the circle such that (PA)(PB)=(PC)(PD) ( as shown in figure ) .

On the basis of above information , answer the questions
If PA=|cosθ+sinθ|andPB=|cosθ−sinθ|, then maximum value of (PC)(PD) , is equal to
View Solution
