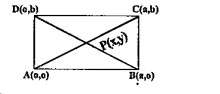
If P be any point in the plane of square ABCD, prove that
PA2+PC2=PB2+PD2 Solution in Gujrati
Step by step video & image solution for If P be any point in the plane of square ABCD, prove that PA^(2)+PC^(2)=PB^(2)+PD^(2) by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
একটি বৃত্তস্থ চতুর্ভুজ ABCD অঙ্কন করো | বর্ধিত AB ও DC বাহুদ্বয় পরস্পরকে P বিন্দুতে ছেদ করলে, প্রমাণ করো যে, PA⋅PB=PC⋅PD
View SolutionA circle is inscribed into a rhombous ABCD with one angle 60. The distance from the centre of the circle to the nearest vertex is equal to 1. If P is any point of the circle then |PA|2+|PB|2+|PC|2+|PD|2 is equal to:
View SolutionABC is an equilateral triangle where AB = a and P is any point in its plane such that PA = PB + PC. Then PA2+PB2+PC2a2 is
View Solutionlf G be the centroid of a triangle ABC and P be any other point in the plane prove that PA2+PB2+PC2=GA2+GB2+GC2+3GP2
View SolutionABCD is a square. P is a point inside the square such that PA=3,PB=7,PD=5. Then area of square ABCD is …………..
View SolutionThere is a point P in a rectangle ABCD, such that PA = 4, PD = 5, PB = 8, find PC.
View SolutionLet ABCD be a square of side length 2 units. Let C1 be the incircle and C2 be the circumcircle of the square ABCD. If P is a point on C1 and Q is a point on C2, the value of PA2+PB2+PC2+PD2QA2+QB2+QC2+QD2 is
View SolutionP is a point inside the rectangle ABCD Prove that PA2+PC2=PB2+PD2:
 .
.
View Solution
