_S01_024_Q01.png)
Water and liquid is filled up behind a square wall of side l
Find out (a). Pressure at A, B and C
(b). Forces in part AB and BC
(c). Total force and point of application of force. (Neglect atmosphere pressure in every calculation.)Solution in Gujrati
_S01_024_S01.png)
_S01_024_S02.png)
(a). As there is no liquid above 'A'
So pressure at A,pA=0
pressure at B,pB=ρgh1
Pressure at C,pC=ρgh1+2ρgh2
(b). Force at A=0
Take strip of width dx at a depth x in part AB
Pressure is equal to ρgx
force on strip=pressure×area
dF=ρgxldx
Total force upto B:Fh1∫0ρgxldx=ρgxlh212=1000×10×10×5×52=1.25×106N
In part BC for force take a elementary strip of width dx in portion BC.
pressure is equal to =ρgh1+2ρg(x−h1)
force on elementary strip=pressure×area dF=[ρgh1+2ρg(x−h1)]ldx
Total force on part BC F=∫lh1[ρgh1+2ρg(x−h1)]ldx
=[ρgh1x+2ρg[x22−h1x]]lh1l
=ρgh1h2l+2ρl[l2−h212−h1l+h21]
=ρgh1h2l+2ρgl2[l2+h21−2h1l]=ρgh1h2l+ρgl(l−h1)2
=ρgh2l[h1+h2]=ρgh2l2=1000×10×5×10×10=5×106N
(c). Total force
Taking torque about A
Total torque of force in AB=∫dF⋅x=∫h10ρgxldx.x
=[ρghlx33]h10=ρglh313=1000×10×10×1253=1.25×1073N−m
Total torque of force in BC =∫dF⋅x
On solving we get =ρgh1h2l[h1+h22]+ρgh22l[h1+2h23]
=1000×10×5×5×10[5+2.5]+1000×10×25×10[5+103]
=2.5×7.5×106+62.53×106=118.753×106
total torque =11.875×1073+1.25×1073=13.125×1073
total torque =total × distance of point of application of force from top =F.xp
6.25×106xp=13.125×1073
xp=7m
Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Elasticity)
16 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 1 (Surface Tension)
21 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
Which one of the following substances possesses the highest elasticity-
View SolutionThe length of needle foating on the surface of water is 1.5 cm the force in addition to its weight required to lift the needle from water surface will be (surface tension of water =7.5N/cm)
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a. Find the total force exerted by the water on the bottom surface of the tank. b. cosider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water. Find the torque of the force calculate in part b. about the bottom edge of this side. e. Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View SolutionA liquid of density ρ is filled upto a geight of 'h' in a container as shown in firgure. Base of the contaimer is a square of side L. Ignoring the atmospheric pressure find

(a) pressure force F1 on its base.
(b) torque of force F1 about an axis passing through C and perpendicular to plane of paper.
(c) Pressure force F2 on the vertical side wall DC.
(d) torque of force F2 about the same axis mentioned in part (b).
(e) point of application of force F2
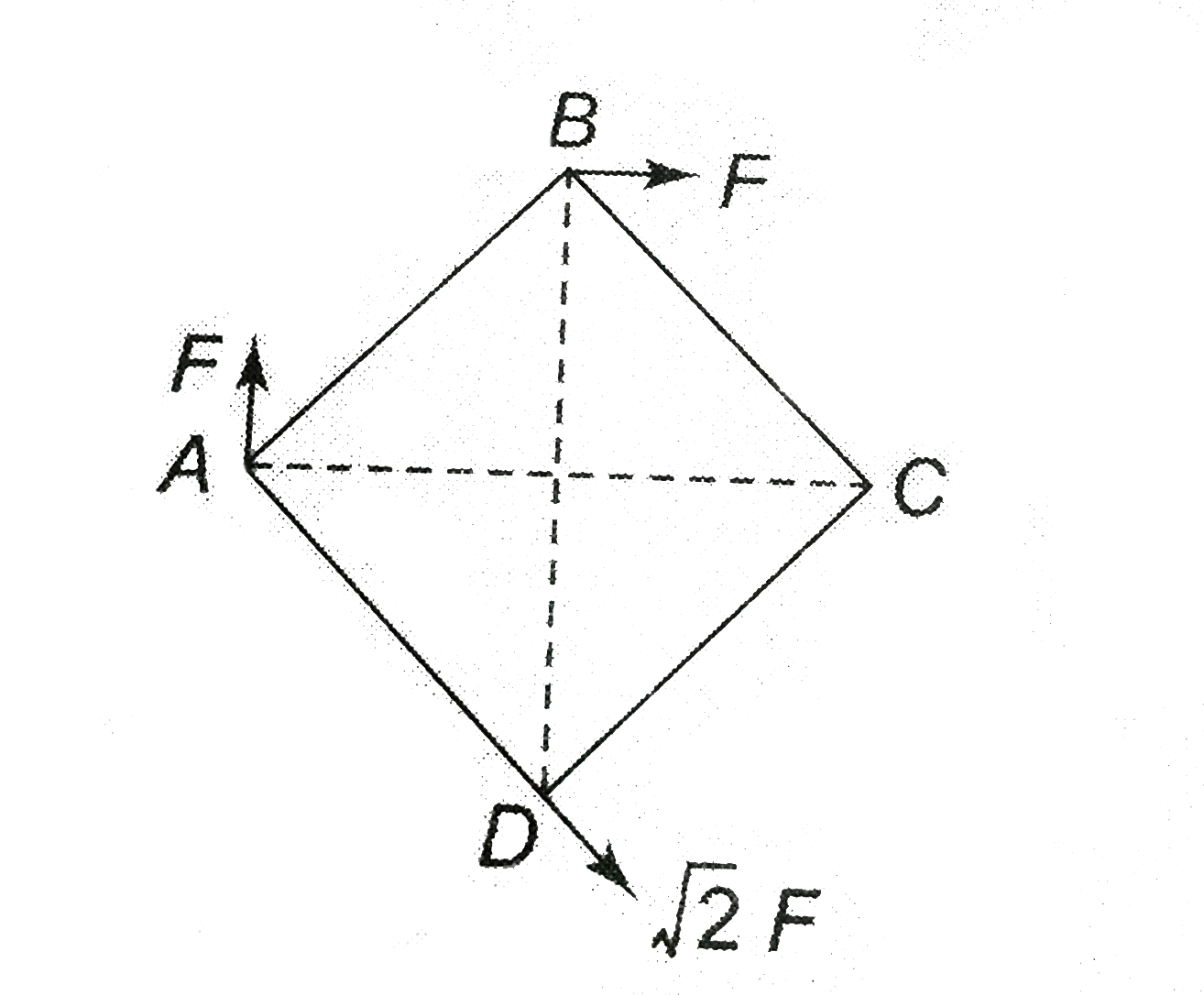
View SolutionThree forces are applied to a square plate as shown in Figure. Find the modulus, direction, and the point of application of the resultant force, if this point is taken on the side BC.

View SolutionThree force are applied to a square plate as shown in the figure. Find the magnitude, direction and point of application of the resultant force if this point is taken on the side BC.
View Solution_S01_055_Q01.png)
A cuboid (a×a×2a) is filled with two immiscible liquid of density 2ρ&ρ as shown in the figure. Neglecting atmospheric pressure ratio of force on base & side wall of the cuboid is
(a). 2:3
(b). 1:3
(c). 5:6
(d). 6:5
View SolutionA tube in vertical plane is shown in figure. It is filled with a liquid of density rho and its end B is closed. Then the force exerted by the fluid on the tube at end B will be : [Neglect atmospheric pressure and assume the radius of the tube to be negligible in comparison to l ]
View SolutionSome liquid is filled in a cylindrical vessel of radius R. Let F_(1) be the force applied by the liquid on the bottom of the cylinder. Now the same liquid is poured into a vessel of uniform square cross-section of side R. Let F_(2) be the force applied by the liquid on the bottom of this new vessel. (Neglect atmosphere pressure). Then
View SolutionA liquid of mass 1 kg is filled in a flask as shown in figure. The force exerted by the flask on the liquid is (g=10m/s2) [Neglect atmospheric pressure]:

View Solution3m×2m×1m आकार के एक आयताकार हौज में ऊपर तक पानी भरा है | (a) पानी द्वारा हौज के फर्श पर लगता कुल बल बताएँ | (b) हौज की 2m×1m वाली एक दीवार पर सतह से x गहराई पर δx चौड़ाई की एक क्षैतिज पट्टी ले | पानी द्वारा इस पट्टी पर लगनेवाले बल निकालें | (c) पिछले भाग में प्राप्त बल का इस दीवार के सबसे निचले किनारे के प्रति बल-आघूर्ण निकालें | (d) पानी द्वारा इस दीवार पर लगता कुल बल निकालें | (e) पानी द्वारा इस दीवार पर लगता कुल बल आघूर्ण निकालें |
वायुमंडलीय दाब को गणना में शामिल न करें और g का मान 10m/s2 ले |
View Solutionदो समान समान्तर बल बिन्दु A और बिन्दु B पर इस प्रकार कार्यरत है कि A पर बल B पर बल से दोगुना है। यदि C परिणामी का कार्य बिन्दु है, तो ACBC है
View SolutionHydrostatics: Pressure due to a Liquid Column | Equating pressure in U-tube Problems | Force and Torque on container wall (point of application of force)
View SolutionWater is filled in a rectangular tank of size 3m×2m×1m. a) Find the total force exerted by the water on the bottom surface of the tank. b) Consider a vertical side of area 2m×1m. Take a horizontal strip of wide δx metre in this side, situated at a depth of x metre from the surface of water.Find the force by the water on this strip. c) Find the torque of the force calculate in part b) about the bottom edge of this side. d) Find the total force by the water on this side. e) Find the total torque by the water on the side about the bottom edge. neglect the atmospheric pressure and take =10ms−2.
View Solution
