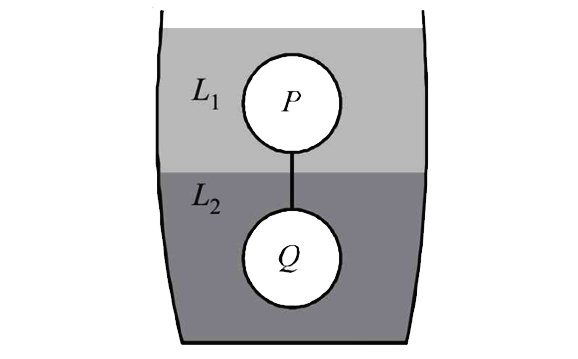
Two spheres P and Q of equal radii have densities ρ1 and ρ2, respectively. The spheres are connected by a massless string and placed in liquids L1 and L2 of densities σ1 and σ2 and viscosities η1 and η2, respectively. They float in equilibrium with the sphere P in L1 and sphere Q in L2 and the string being taut(see figure). If sphere P alone in L2 has terminal velocity →Vp and Q alone in L1 has terminal velocity →VQ, then
 Solution in Gujrati
Solution in Gujrati
∣∣→VP∣∣∣∣→VQ∣∣=η1η2
∣∣→VP∣∣∣∣→VQ∣∣=η2η1
→VP.→VQ>0
→VP.→VPQ<0
The correct Answer is:A, D
Step by step video & image solution for Two spheres P and Q of equal radii have densities rho_1 and rho_2, respectively. The spheres are connected by a massless string and placed in liquids L_1 and L_2 of densities sigma_1 and sigma_2 and viscosities eta_1 and eta_2, respectively. They float in equilibrium with the sphere P in L_1 and sphere Q in L_2 and the string being taut(see figure). If sphere P alone in L_2 has terminal velocity vecV_p and Q alone in L_1 has terminal velocity vecV_Q, then by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Comprehension)
5 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Assertion Reason)
1 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (MCQ)
13 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
Similar Questions
A wooden cylinder of diameter 4 r, height H and density ρ/3 is kept on a hole of diameter 2 r of a tank, filled with water of density ρ as shown in the

If level of liquid starts decreasing slowly, when the level of liquid is at a height h1 above the cylinder, the block just start moving up. Then the value of h1 is
View SolutionSTATEMENT-1: The stream of water flowing at high speed from a garden hose pipe tends to spread like a fountain when held vertically up, but tends to narrow down when held vertically down.
STATEMENT-2: In any steady flow of an incompressible fluid, the volume flow rate of the fluid remains constant.
View SolutionWater from a tap emerges vertically downwards with an initial spped of 1.0ms−1. The cross-sectional area of the tap is 10−4m2. Assume that the pressure is constant throughout the stream of water, and that the flow is steady. The cross-sectional area of the stream 0.15 m below the tap is
View SolutionTwo particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionTwo spheres P and Q of equal radii have densities rho_1 and rho_2 , respectively. The spheres are connected by a massless string and placed in liquids L_1 and L_2 of densities sigma_1 and sigma_2 and viscosities eta_1 and eta_2 , respectively. They float in equilibrium with the sphere P in L_1 and sphere Q in L_2 and the string being taut(see figure). If sphere P alone in L_2 has terminal velocity vecV_p and Q alone in L_1 has terminal velocity vecV_Q , then
View SolutionConsider two solid spheres P and Q each of density 8gm cm^-3 and diameters 1cm and 0.5cm, respectively. Sphere P is dropped into a liquid of density 0.8gm cm^-3 and viscosity eta=3 poiseulles. Sphere Q is dropped into a liquid of density 1.6gmcm^-3 and viscosity eta=2 poiseulles. The ratio of the terminal velocities of P and Q is
View SolutionTwo non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
View SolutionA sphere of radius R and density rho_1 is dropped in a liquid of density sigma . Its terminal velocity is v_1 . If another sphere of radius R and density rho_2 is dropped in the same liquid, its terminal velocity will be:
View SolutionIn Fig., there are two convex lenses L_1 and L_2 having focal lengths F_1 and F_2 respectively. The distance between L_1 and L_2 will be : .
View SolutionThe lengths of two intersecting wires of the same radius are respectively l_1 Oh l_2 And the radiance of their components, respectively rho_1 Oh rho_2 If two of them are added to a class co-operative, there will be an equivalent radius (rho_1l_2+rho_2l_1)/(rho_1+rho_2) (rho_1l_1+rho_2l_2)/(l_1+l_2) (rho_1l_1-rho_2l_2)/(l_1-l_2) (rho_1l_2+rho_2l_1)/(l_1+l_2)
View SolutionTwo wires of same radius having lengths l_1 , and l_2 and resistivities rho_1 and rho_2 are connected in series. The equivalent resistivity will be
View SolutionL1andL2 are two intersecting lines. If the image of L1 w.r.t. L2 and that of L2 w.r.t. L1 concide, then the angle between L1andL2 is
View SolutionR व 2R त्रिज्या वाले दो अचालक ठोस गोलों को जिन पर क्रमशः ρ1 तथा ρ2 एकसमान आयतन आवेश घनत्व है, एक दूसरे से स्पर्श करते हुए रखा गया है। दोनों गोलों के केंद्रों को जोड़ने वाली रेखा के अनुदिश छोटे गोले के केंद्र से 2R दूरी पर कुल विद्युत क्षेत्र शून्य है। तब अनुपात ρ1ρ2 का मान हो सकता है:
View SolutionTwo non-conducting solid spheres of radii R and 2R, having uniform volume charge densities ρ1 and ρ2 respectively, touch each other. The net electric field at a distance 2R from the centre of the smaller sphere, along the line joining the centres of the spheres, is zero. The ratio ρ1ρ2 can be
View SolutionTwo sphere (1) and (2) connected by a lifht string AB are floating in a liquid with the string vertical as shown In figure. Average density of spheres (1) and (2) are d and 2d respectively and the ration of their volumes is 3 : 1. Then
View Solution
