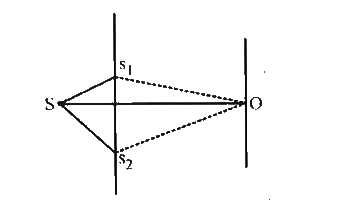
Let S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be (assume θ to be a small angle)Solution in Gujrati
λ/θ
λθ
2λ/θ
λ/2θ
The correct Answer is:A
_E01_034_S01.png)
As distance between S1 & S2 is very much medium. And equal to 'd' so the angle made at 'P' is very much small
∴ angle =ArcD⇒θ=dD
∴ fringe width =λDd=λθ(∵dD=θ)
Topper's Solved these Questions
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Brain Teasures)
22 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Exercise 3 (Miscellaneous type Questions)
27 Videos
- WAVE OPTICSBOOK - ALLEN CHAPTER - WAVE OPTICSEXERCISE - Example 15
1 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
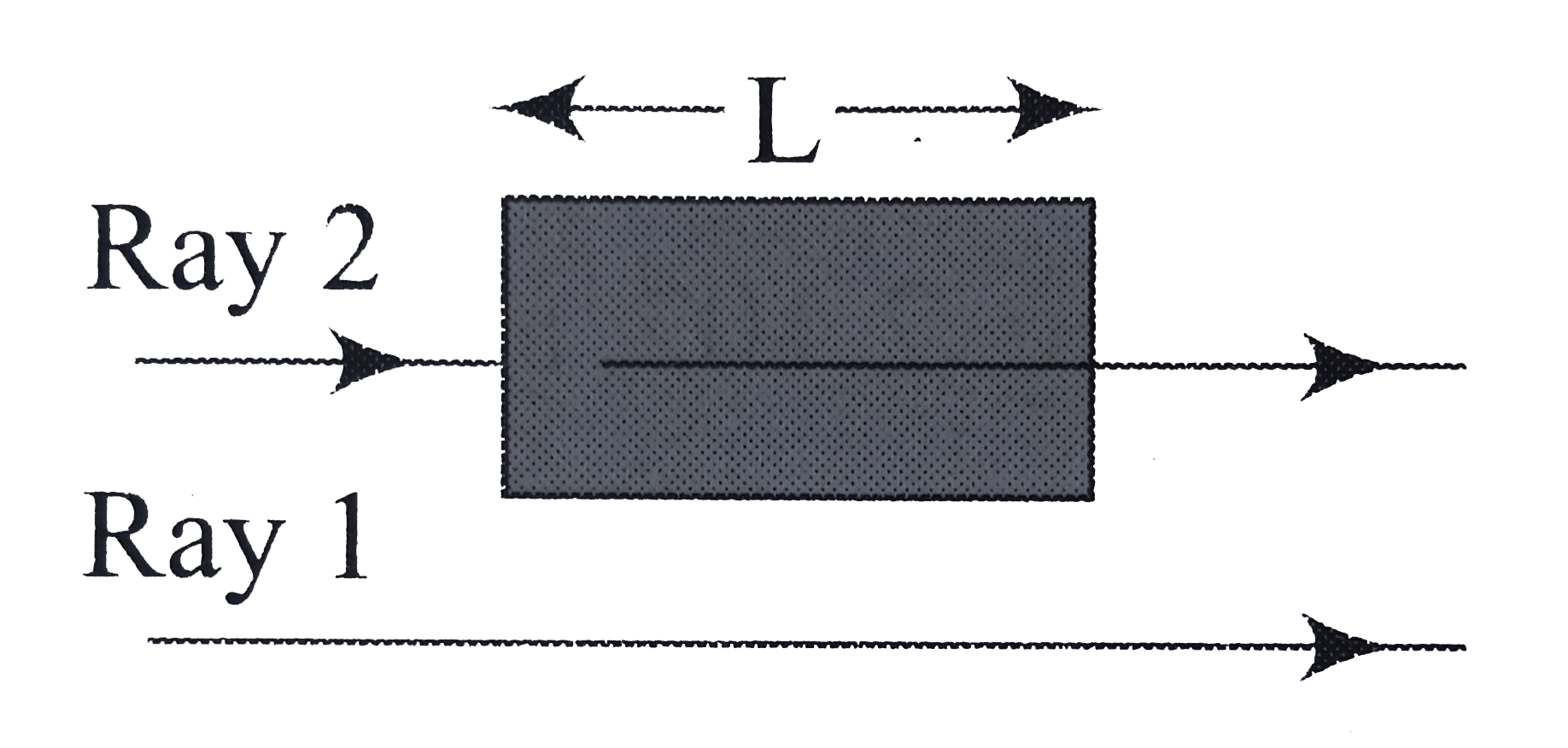
As shown in figure waves with identical wavelengths and amplitudes and which are intially in phase travel through difference media. Ray 1 travels through air and Ray 2 through a transparent medium for equal length L, in four different situations. Rays reach a common point on the screen. The number of wavelengths in length L is N2 for Ray 2 and N1 for Ray 1. In the following table, values of N1 and N2 are given for all four situations. The order or the situations according to the intensity of the light at the common point in descending order is Situations
1 2 3 4
N1 2.75 1.80 3.00 3.25
N2 2.75 2.80 3.25 4.00
View SolutionStatement-1: if white light is used in YDSE, then the central bright fringe will be white.
Statement-2: In case of white light used in YDSE all the wavelengths produce their zero order maxima at the same position.
View Solution_S01_033_Q01.png)
In a typical young's double slit experiment a point source of monochromatic light is kept as shown in the figure. If the source is given an instantaneous velocity v=1 mm per second towards the screen, then the instantaneous velocity of central maxima is given as α×10−βcm/s upward in scientific notation find the value of α+β
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionLet S_1 and S_2 be the two slits in Young's double slit experiment. If central maxima is observed at P and angle S_1 P S_2 = theta , ( theta is small) find the y-coordinates of the 3rd minima assuming the origin at the central maxima. ( lambda = wavelength of monochromatic light used).
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then fringe width for the light of wavelength λ will be (assume θ to be a small angle)
View SolutionIn a Young's double-slit experiment, let S_(1) and S_(2) be the two slits, and C be the centre of the screen. If /_S_(1)CS_(2)=theta and lambda is wavelength, the fringe width will be
View SolutionIn a Young's double slit experiment, let S_(1) and S_(2) be the two slits, and C be the centre of the screen. If angle S_(1)CS_(2)=theta and lambda is the wavelength, the fringe width will be
View SolutionIn an interference experiment, the two slits S1andS2 are not equidistant from the source S. then the central fringe at 0 will be
View SolutionIn Young's double slit experiment, an interference pattern is obtained on a screen by a light of wavelength 6000 overset(circ)(A) coming from the coherent sources S_(1) and S_(2) . At certain point P on the screen third dark fringe is formed. Then, the path difference S_(1) P – S_(2) P in micron is
View SolutionAt two points P and Q on a screen in Young's double slit experiment, waves from slits S_(1) and S_(2) have a path difference of 0 and (lambda)/(4) respectively. The ratio of intensities at P and Q will be
View SolutionLet S1 and S2 be the two slits in Young's double-slit experiment. If central maxima is observed at P and angle ∠S1PS2=θ, then the fringe width for the light of wavelength λ will be (assume θ to be a small angle)
View SolutionAt two points P and Q on a screen in Young's double slit experiment, waves from slits S1andS2 have a path difference of O and λ4 respectively. The ratio of intensities at P and Q will be ......
View SolutionLet S_(1) and S_(2) be the two slits in Young.s double slit experiment . If central maxima is observedat P and angle angleS, P_(2)= theta then the fringe width for the light of wavelength lambda will be (assume theta to be a small angle )
View SolutionIn a Young's double slit experiment, let S1 and S2 be the two slits, and C be the centre of the screen. If ∠S1CS2=θ and λ is the wavelength, the fringe width will be
View Solution
