A sonometer wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass of 1 kg. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.Solution in Gujrati
The correct Answer is:0.073m/s
μ=1gm10cm=10−3kg0.1m=10−4kg/m,T=64N
v=√Tμ⇒f0=v2L=12×0.1√6410−4
=5×8×100
=4000m/s
⇒vstring=vfork=1
=5×8×100
=4000m/s
⇒vstring=vfork=1
⇒4000−4000(300300−v)=1⇒v=0.073m/s.
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
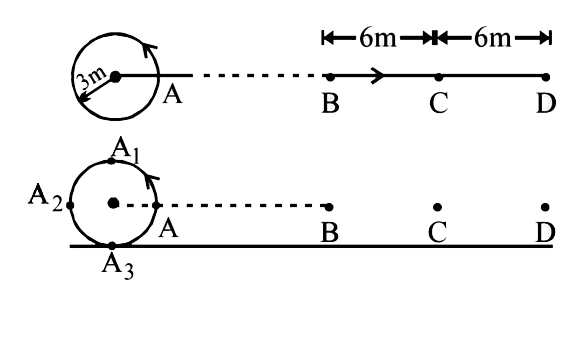
A source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionTube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionStatement-1 : Sound travels faster in moist air
Statement-2 : The density of moist air is less then density of dry air.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA sonometer wire under tension of 64 N uibrating in its fundamental mode is in resonance with a uibrating tuning fork . The uibrating portion of the sonemether wire has a length of 10 cm and mass of 1 g . The uibrating tuning fork is now moved away from the uibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second . Calculate the speed with which the tuning fork is moved , if speed of sound in air is 300 m//s .
View SolutionA sonometer wire under tension of 63 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of that sonometer wire has a length of 10 cm and a mass of 1 g. The vibrating tuning fork isnow moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved if the pseed of sound in air is 300 m/s.
View SolutionA sonometer wire under tension of 128 N vibrates in resonance with a tuning fork . The vibrating portion of sonometer wire has length of 20 cm and mass 1 g . The vibrating wire at constant speed of 0.75 m//s and an observer standing near the sonometer hear 1 beat//s . Find the speed of sound in air.
View SolutionA sonometer wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass of 1 kg. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near the sonometer hears one beat per second. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.
View SolutionA given length of sonometer wire is in resonance with a tuning fork. If the length of the wire is reduced by 4% the wire vibration with the fork produces 8 beats per second. The frequency of the tuning fork is
View SolutionThe fundamental frequency of a sonometer wire is 200 Hz.
It is found that a tuning fork of frequency 400 Hz produces resonant vibrations in the same wire . Then the wire vibrates with
View SolutionA sonometer wire vibrating in its fundamental mode, is in unison with a tuning fork when the length of the wire between the bridges is 25 cm. By keeping the same tension , the length between the bridges is increased to 75 cm. The tuning fork can still be in resonance with the vibrating wire , provided the wire vibrates with
View SolutionWhen a vibration tuning fork is placed on a sound box of a sonometer, 8 beats per second are heard when the length of the sonometer wire is kept at 101cm or 100cm. Then the frequency of the tuning fork is (consider that the tension in the wire is kept constant)
View SolutionWhen a vibrating tuning fork is placed on a sound box of a sonometer, 8 beats per second are heard when the length of the sonometer wire is kept at 101cm or 100cm. Then the frequency of the tuning frok is (consider that the tension in the wire is kept constant)
View SolutionA sonometer wire under tension of 64N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of that sonometer wire has a length of 10cm and a mass of 1 gm. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near sonometer hears one beat per second. The speed with which the tuning fork is moved is 752 xx 10^(-y) (speed of sound in air is 300 m/s). Then y
View SolutionA stretched wire under tension of 64 N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of the sonometer wire has a length of 10 cm and mass lg. The vibrating tuning fork in now moved away from the vibrating wire at a constant speed and an observer standing near the sonometer hears one beat per sec. Calculate the speed with which the tuning fork is moved, if the speed of sound in air is 300 m/s.
View SolutionA sonometer wire under tension of 64N vibrating in its fundamental mode is in resonance with a vibrating tuning fork. The vibrating portion of that sonometer wire has a length of 10cm and a mass of 1 gm. The vibrating tuning fork is now moved away from the vibrating wire with a constant speed and an observer standing near sonometer hears one beat per second. The speed with which the tuning fork is moved is 752×10y (speed of sound in air is 300 m/s). Then y
View Solution
