A string vibrate according to the equation y=5sin(πx3)cos(40πt) where x and y in cm's and t is in second.
(i) What is the equation of incident and reflected wave ?
(ii) What is the distance between the adjacent nodes ?
(iii) What is the velocity of the particle of the string at the position x = 1.5 cm when t=98sec ?Solution in Gujrati
The correct Answer is:(i) yincident=2.5sin(40πt+π3x)andyreflected=−2.5sin(40t−π3x)
(ii) 3 cm
(iii) 0
y=2sin(πx3)cos(40π)
=2.5sin(40π+πx3)−2.5sin(40πt−πx3)
(i) Equation of incident wave
y1=2.5sin(40πt+πx3)
Equation of reflected wave
y2=−2.5sin(40πt−πx3)
(ii) 2πλ=π3⇒λ=6cm
∴ Distance between adjacent nodes =3cm
(iii) v=−5(40π)sin(πx3)sin(40πt)
=−200πsin(π×1.53)sin(40π×98)=0
Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[A]
28 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-03)
31 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
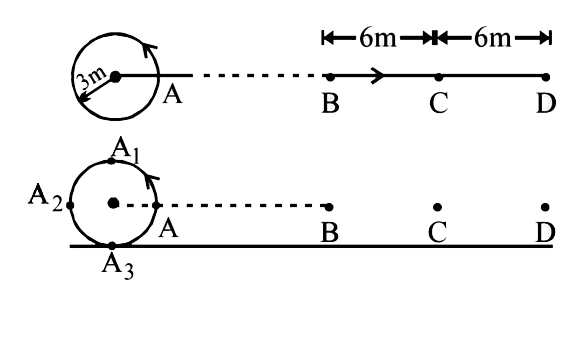
A source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
View SolutionTube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionStatement-1 : Sound travels faster in moist air
Statement-2 : The density of moist air is less then density of dry air.
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionA stationary wave is given by y = 5 sin (pi x)/( 3) cos 40 pi t where x and y are in cm and t is in second. a. What are the amplitude and velocity of the component wave whose superposition can give rise to this vibration ? b. What is the distance between the nodes ? c. What is the velocity of a particle of the string at the position x = 1.5 cm when t = 9//8 s ?
View SolutionA string vibrate according to the equation y = 5 sin ((pi x)/(3)) cos (40 pi t) where x and y in cm's and t is in second. (i) What is the equation of incident and reflected wave ? (ii) What is the distance between the adjacent nodes ? (iii) What is the velocity of the particle of the string at the position x = 1.5 cm when t = (9)/(8) sec ?
View SolutionThe equation of stationary wave along a stretched string is given by y=5sin(πx)3cos40πt, where x and y are in cm and t in second. The separation between two adjacent nodes is
View SolutionA string vibrates according to the equation y=5sin(2πx3)cos20πt, where x and y are in cm and t in sec . The distance between two adjacent nodes is
View SolutionThe equation of stationary wave along a stretched string is given by y = 5 sin(pi x)/(3) cos 40pi t where x and y are in centimetre and t in second. The separation between two adjacent nodes is :
View SolutionA standing wave is given by y=5sinπx20cos40πt, where x and y are in cm and t is in second. What is the minimum distance between a node and the adjacent antinode ?
View SolutionA vibrating string is tied at its two ends. The equation of the wave produced on the string is given by y=cos(2πt)sin(2πx)
What is the lenghts of the string,f it is in the fundamental node of vibration ?
View SolutionThe equation of stationary wave along a stretched string is given by y=5sin(πx)3cos40πt where x and y are in centimetre and t in second. The separation between two adjacent nodes is :
View SolutionA stationary wave is given by y = 5 sin (pi x)/(3) cos 40 pi t where x and y are in cm and t is in seconds What is the distance between two successive nodes
View SolutionA stationary wave is given by y=5sin(πx)3cos40πt where x and y are in cm and t is in seconds
What is the velocity of a particle of the string at the position x = 1.5 cm when t=98s
View Solutionतने हुए धागे की अप्रगामी तरंग का समीकरण y=7sinπx3cos30πt द्वारा व्यक्त की जाती है, जहाँ x य y सेमी में व t सैकंड में है। दो क्रमिक निस्पन्दो के बीच की दूरी है
View Solution
