The (x,y) co-ordinates of the corners of a square plate are (0,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)Solution in Gujrati
acos(πx2L)cos(πy2L)
asin(πxL)sin(πyL)
asin(πxL)sin(2πyL)
acos(2πxL)sin(πyL)
The correct Answer is:B, C
Since, the edges are clamed, displacement of the edges u(x,y)=0 for
_E01_191_S01.png)
Line OA i.e. y=00≤x≤LAB i.e x=L0≤y≤LBC i.e y=L0≤x≤LOC i.e x=00≤y≤L
The above conditions are satisfied only i nalternatives (b) and (c)
Now that u(x,y)=0 , for all four value e.g. in alternative (d),u(x,y)=0 for y=0,y=L but is not zero for for x =0 or x =L, Similarly in option (a) u (x,y) =0 at x=L,y=L but it is not zero for x = 0 or y = 0 while options (b) and (c), u(x,y)=0 for x=0,y=0,x=L and y=L
Topper's Solved these Questions
Similar Questions
Tube A has both ends open while tube B has one closed, otherwise they are identical. The ratio of fundamental frequency of tube AandB is
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionThe (x, y) co-ordinates of the corners of a square plate are (0, 0) , (L, L) and (0, L) . The edges of the plate are clamped and transverse standing waves are set up in it. If u(x, y) denotes the displacement of the plate at the point (x, y) at some instant of time, the possible expression (s) for u is (are) (a = posotive constant)
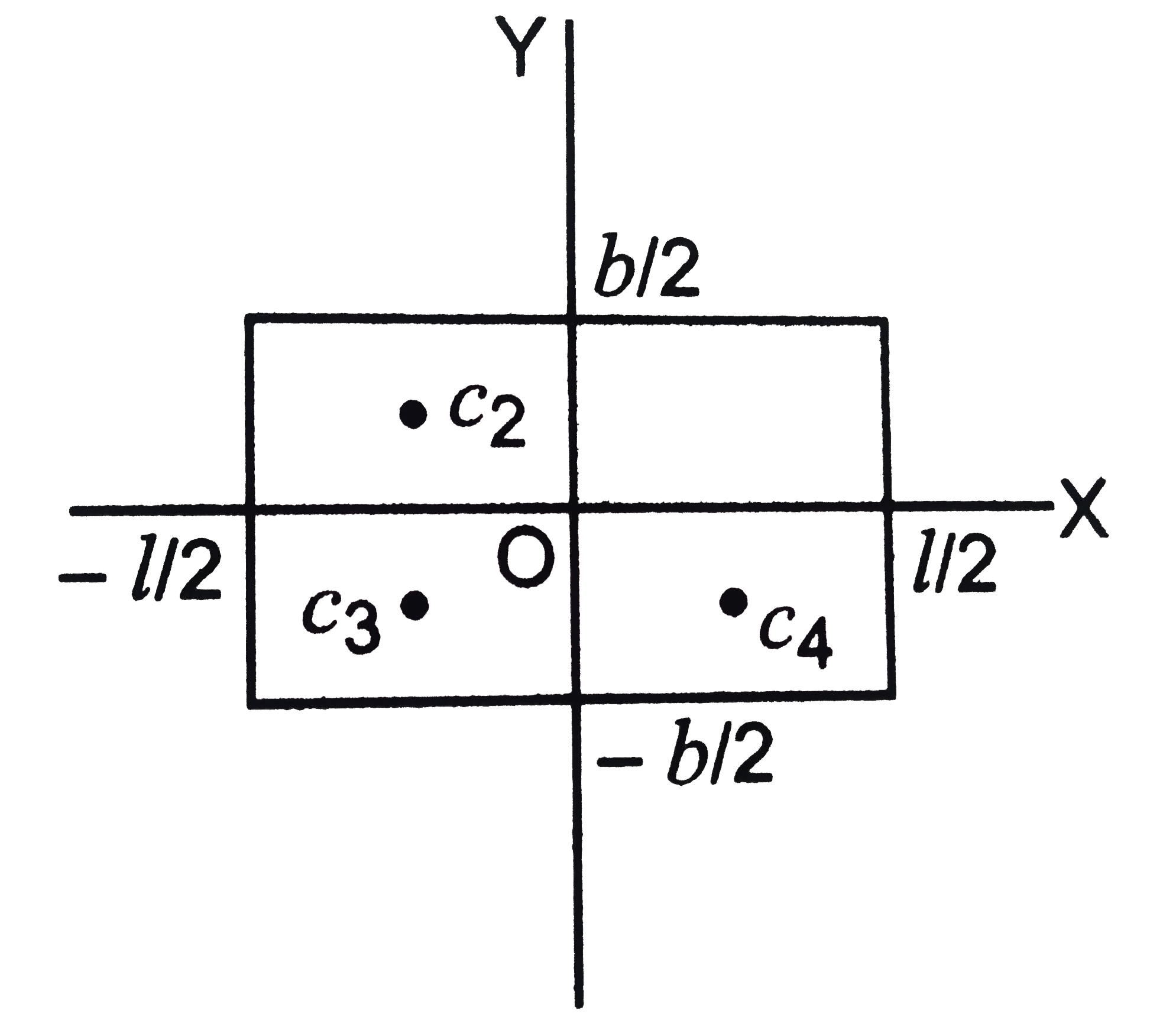
View SolutionA rectangular plate of dimensions l×b is in x−y plane as shown in Fig. If the portion of this plate lying in quadrant I is removed, find the position of centre of mass of remaining part of plate.
View SolutionA string with tension T and mass per unit length mu is clamped down at x=0 and at x=L. at t=0, the string is at rest and displaced in the y-direction y(x,0)=2"sin"(2pix)/(L)+2"sin"(pix)/(L) Q. What is the total energy at t=0?
View Solutionएक वर्गाकार प्लेट की कोनों के (x,y) निर्देशांक (0,0), (L,0), (L,L) तथा (0,L) है। प्लेट के कोने कसे है तथा इसमें अनुप्रस्थ अप्रगामी तरंगे उत्पन्न की जाती है। यदि किसी क्षण बिन्दु (x,y) पर प्लेट का विस्थापन u (x,y) से व्यक्त किया जाता है तो u के / का सम्भव व्यंजक है / है (a = धन नियतांक )
View SolutionIf u=cos−1(xy) prove that x∂u∂x+y∂u∂y=0.
View SolutionThe (x, y) coordinates of the corners of a square plate are (0,0), (L,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set-up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression(s) for u is (are) (a=positive constant)
View SolutionA flat square surface with sides of length L is described by the equations x = L, 0 lt y lt L,0 lt z lt L Find the electric flux through the square due to a positive point charge q located at the origin (x = 0, y = 0 z = 0)
View SolutionThe (x, y) coordinates of the corners of a square plate are (0,0), (L,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set-up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression(s) for u is (are) (a=positive constant)
View Solutionएक वर्गाकार प्लेट के (x,y) निर्देशांक (0,0) (L, 0) (L, L) तथा (0, L) है । प्लेट की भुजाओं को दृढित करके इसमें एक अप्रगामी तरंग उत्पन्न की जाती है। यदि u(x, v) प्लेट के (x, y) बिन्दु पर किसी क्षण विस्थापन है तो u के लिये सत्य है-(a = धनात्मक स्थिरांक)
View SolutionFind the distance between parallel lines:- l(x+y)+p=0 and l(x+y)−r=0.
View SolutionFind the distance between the parallel lines l (x + y) +p = 0 and l (x + y) - r = 0
View Solutionਸਮਾਂਤਰ ਰੇਖਾਵਾਂ ਦੇ ਵਿਚਕਾਰ ਦੂਰੀ ਪਤਾ ਕਰੋ:- l(x+y)+p=0 ਅਤੇ l(x+y)−r=0.
View SolutionThe (x,y) co-ordinates of the corners of a square plate are (0,0),(L,0), (L,L) and (0,L). The edges of the plate are clamped and transverse standing waves are set up in it. If u(x,y) denotes the displacement of the plate at the point (x,y) at some instant of time, the possible expression (s) for u is (are) (a=positiveconstant)
View Solution
