Mass center of composite bodies
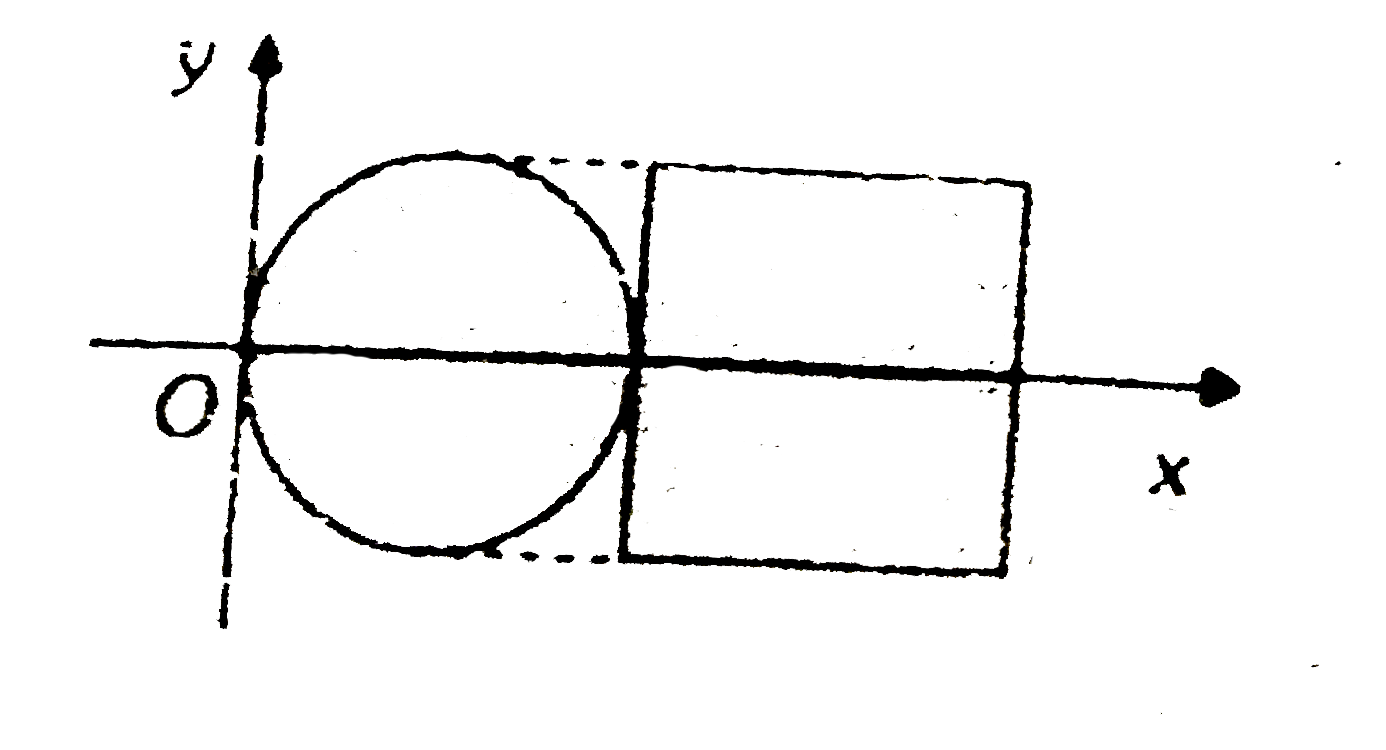
A composite body is made of joining two or more bodies. Find mass center of the following composite body made by joining a uniform disk of radius r and a uniform square plate of the same mass per unit area.Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

To find mass center the component bodies are assumed particle of masses equal to corresponding bodies located on the respective mass centers. Then we use equation to find the coordinates of the mass center of the composite body.
To find mass center of the composite body, we first have to calculate mases of the bodies, because mass distribution is given.
If we denote surface mass density (mass per unit area) by $σ$ , masses of the bodies are
$\begin{matrix} Mass of the disk & m_{d} = Mass per unit area \times Area = σ (π r^{2}) = σ π r^{2} \\ Mass of the square plate & m_{p} = Mass per unit area \times Area = σ (4 r^{2}) = 4 σ r^{2} \\ Location of mass centre of the disk & x_{d} = Centre of the disk = r and y_{d} = 0 \\ Location of mass centre of the square plante & x_{p} = Center of the surface plate = 3 r and y_{p} = 0 \end{matrix}$
Using eq. , we obtain coordinates $(x_{c}, y_{c})$ of the composite body. $x_{c} = \frac{m_{d} x_{d} + m_{s} x_{s}}{m_{d} + m_{s}} = \frac{r (π + 12)}{(π + 4)}$
and $y_{c} = \frac{m_{d} x_{d} + m_{s} x_{s}}{m_{d} + m_{s}} = 0$
Coordinates of the mass center are $(\frac{r (π + 12)}{(π + 4)}, 0)$

|

Class 11 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION

Topper's Solved these Questions

Similar Questions

ALLEN -CENTRE OF MASS-EXERCISE-V B

Home
Ask Doubt
Profile