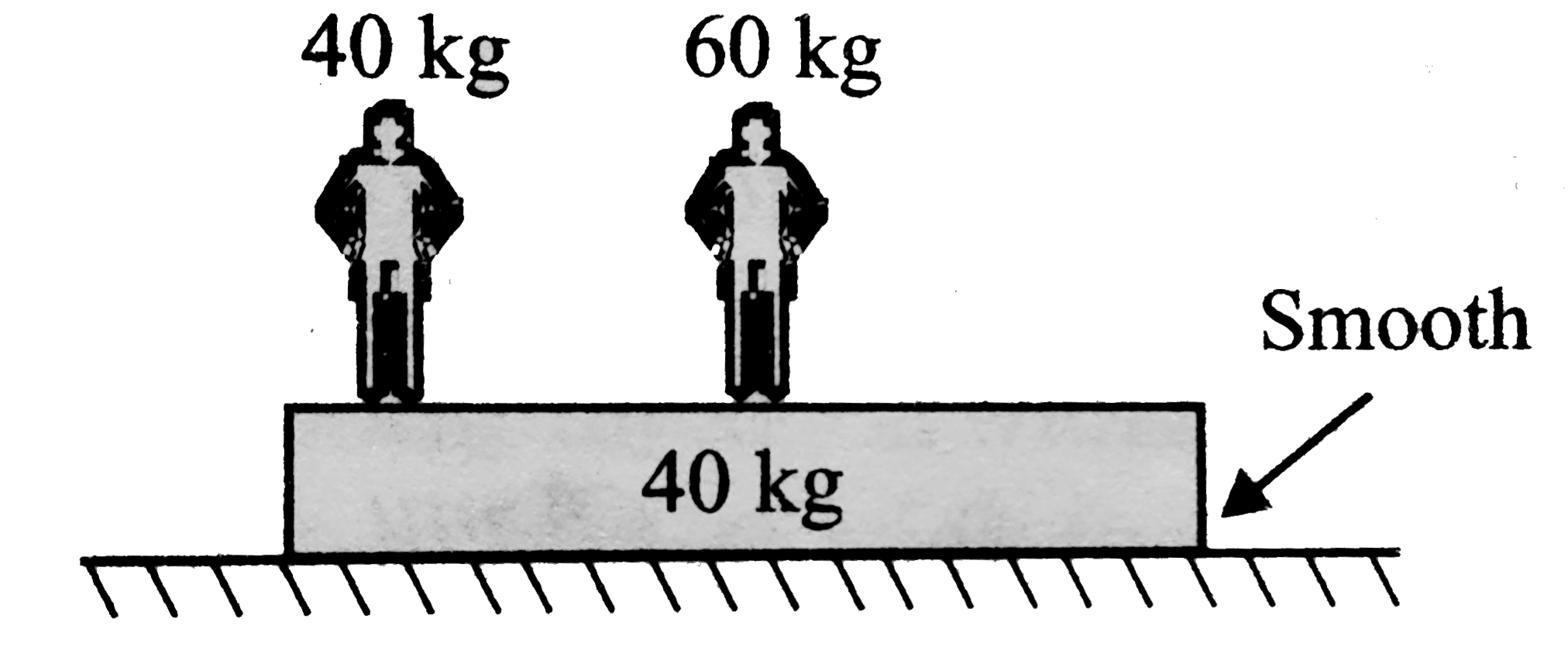
Two men 'A' and 'B' are standing on a plank. 'B' is at the middle of the plank and 'A' is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. 'A' and 'B' start moving such that the position of 'B' remains fixed with respect to ground, then 'A' meets 'B'. Then the point where A meets B is located at
Solution in Gujrati
the middle of the plank
30cm from the left end of the plank
the right end of the plank
None of these
The correct Answer is:C
In the ground frame
:mAΔxA+mBΔxB+mPΔxP=0
⇒40×60+0+40×ΔxP=0
⇒ΔxP=−60 (to the left)
Hence A & B meet at the right end.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III41videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A32videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I40videos
CENTRE OF MASS
- BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON11videos
BASIC MATHEMATICS USED IN PHYSICS &VECTORS
- BOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)3videos
ELASTICITY, SURFACE TENSION AND FLUID MECHANICS
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
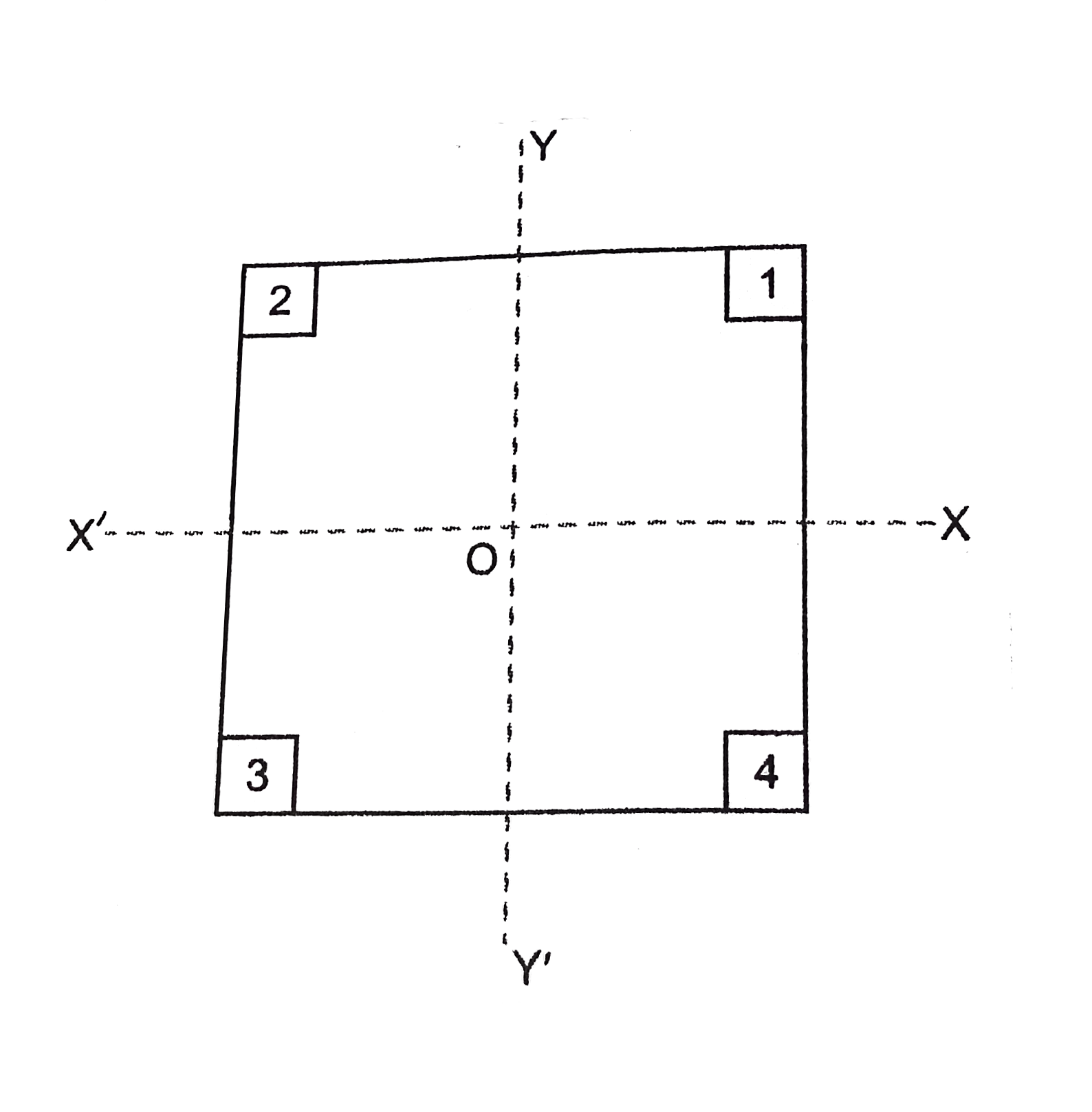
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None03:45View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
04:55View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
02:06View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.02:29View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
02:29View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M//3 , the distance that the man moves relative to the ground is
02:17View SolutionA man of mass m moves on a plank of mass M with a constant veloicty u with respect to the plank, as shown in figure.
a.If the plank rest on smooth horizontal surface, determine the velocity of the plank.
b If the man travels a distasnce L with respect to the plank, find the distance travelled by the plank with respect to te ground.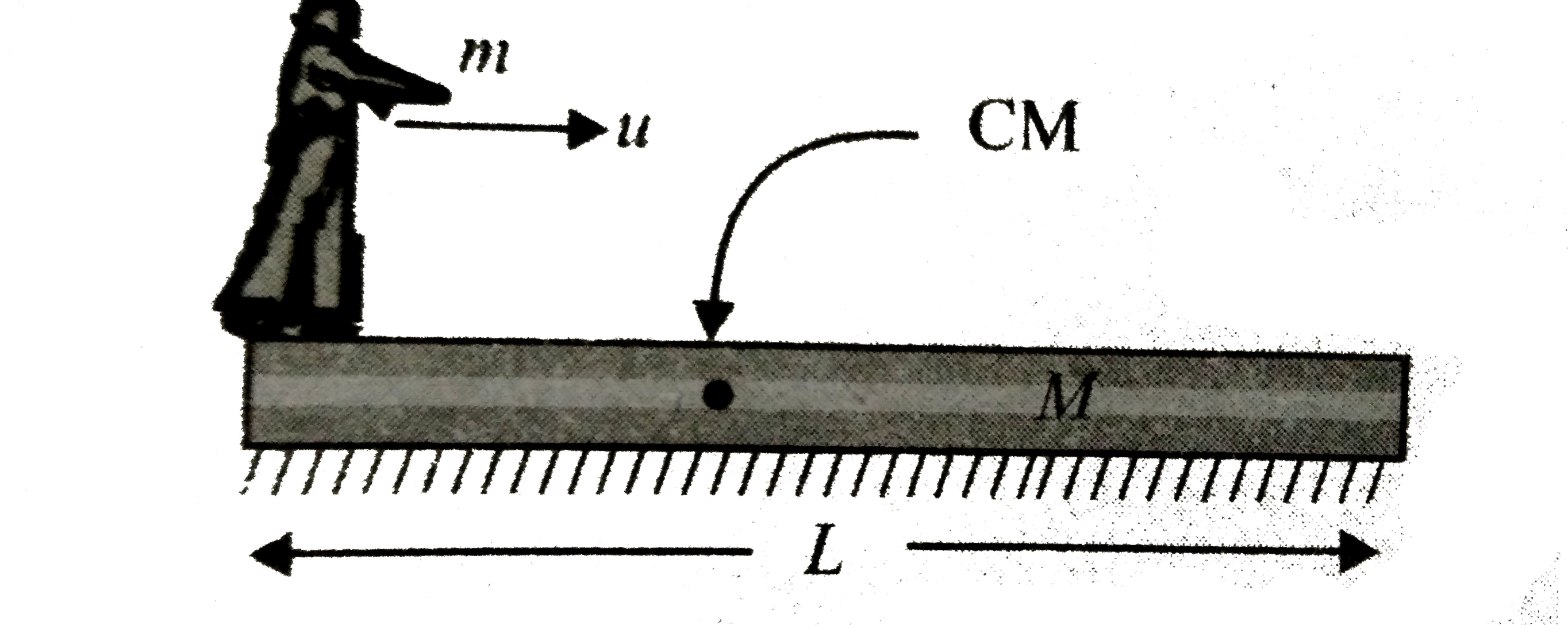
02:29View SolutionTwo men 'A' and 'B' are standing on a plank. 'B' is at the middle of the plank and 'A' is at the left end of the plank. Lower surface of the plank is smooth. System is initially at rest and masses are as shown in Fig. 'A' and 'B' start moving such that the position of 'B' remains fixed with respect to ground, then 'A' meets 'B'. Then the point where A meets B is located at
01:37View SolutionBlock A of mass m is placed on a plank B . A light support S is fixed on plank B and is attached with the block A with a spring of spring constant K. Consider that initialy spring is in the natural length, and the system is at rest. Find the maximum compression in the spring, if the plank B is moved with a constant acceleration 'a' . (All the surface are smooth) :
02:48View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
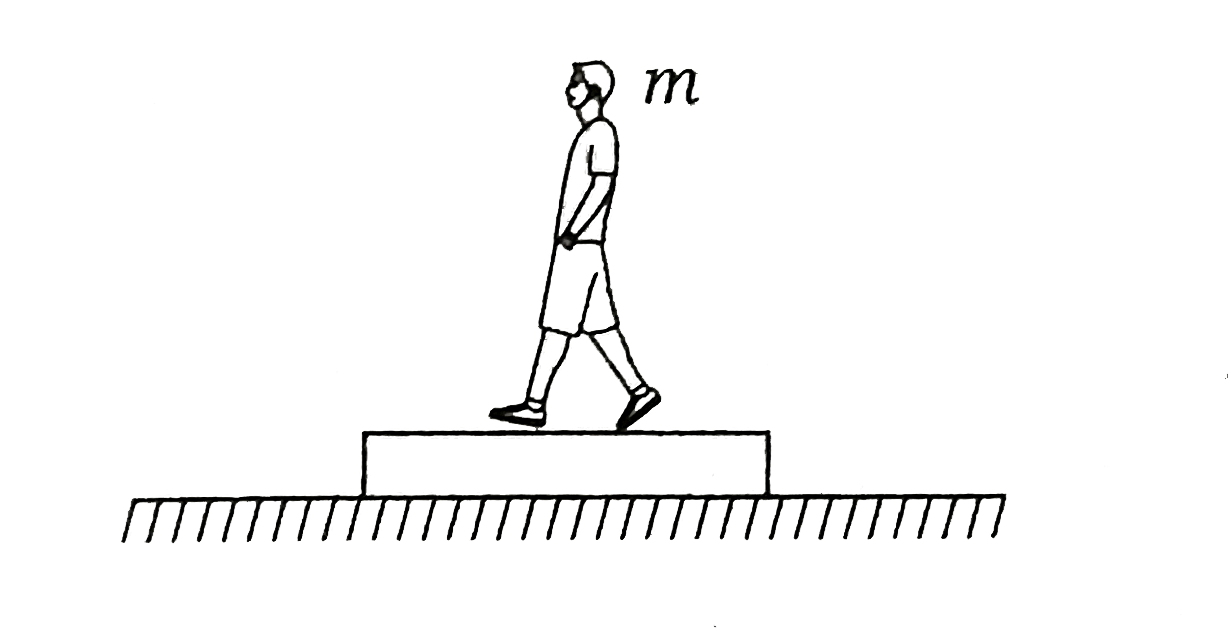
01:37View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
03:51View SolutionA man of mass M stands at one end of a plank of length L Which lies at rest on a frictionless surface . The man walks to the other end of the plank. If the mass of the plank is 3M, the distance that the man moves relative to the ground is
02:52View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
02:58View SolutionA man of mass m is standing on a plank of equal mass m resting on a smooth horizontal surface. The man starts moving on the plank with speed u relative to the plank. The speed of the man relative to the ground is
02:30View SolutionA man of mass M stands at one end of a stationary plank of length L, lying on a smooth surface. The man walks to the other end of the plank. If the mass of the plank is M/3, the distance that the man moves relative to the ground is
04:41View SolutionA man of mass m moves on a plank of mass M with a constant veloicty u with respect to the plank, as shown in figure. a.If the plank rest on smooth horizontal surface, determine the velocity of the plank. b If the man travels a distasnce L with respect to the plank, find the distance travelled by the plank with respect to te ground.
02:50View Solution