A bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle θ with the wire, the bead will have slipped a dsitance.
 Solution in Gujrati
Solution in Gujrati
L(1−cosθ)
(L2)(1−cosθ)
(L3)(1−cosθ)
(L6)(1−cosθ)
The correct Answer is:C
Let x= displacement of ring to the left
⇒Δxcm=2mx+m(x+L−Lcosθ)3m=0
⇒x=−13(1−cosθ)
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
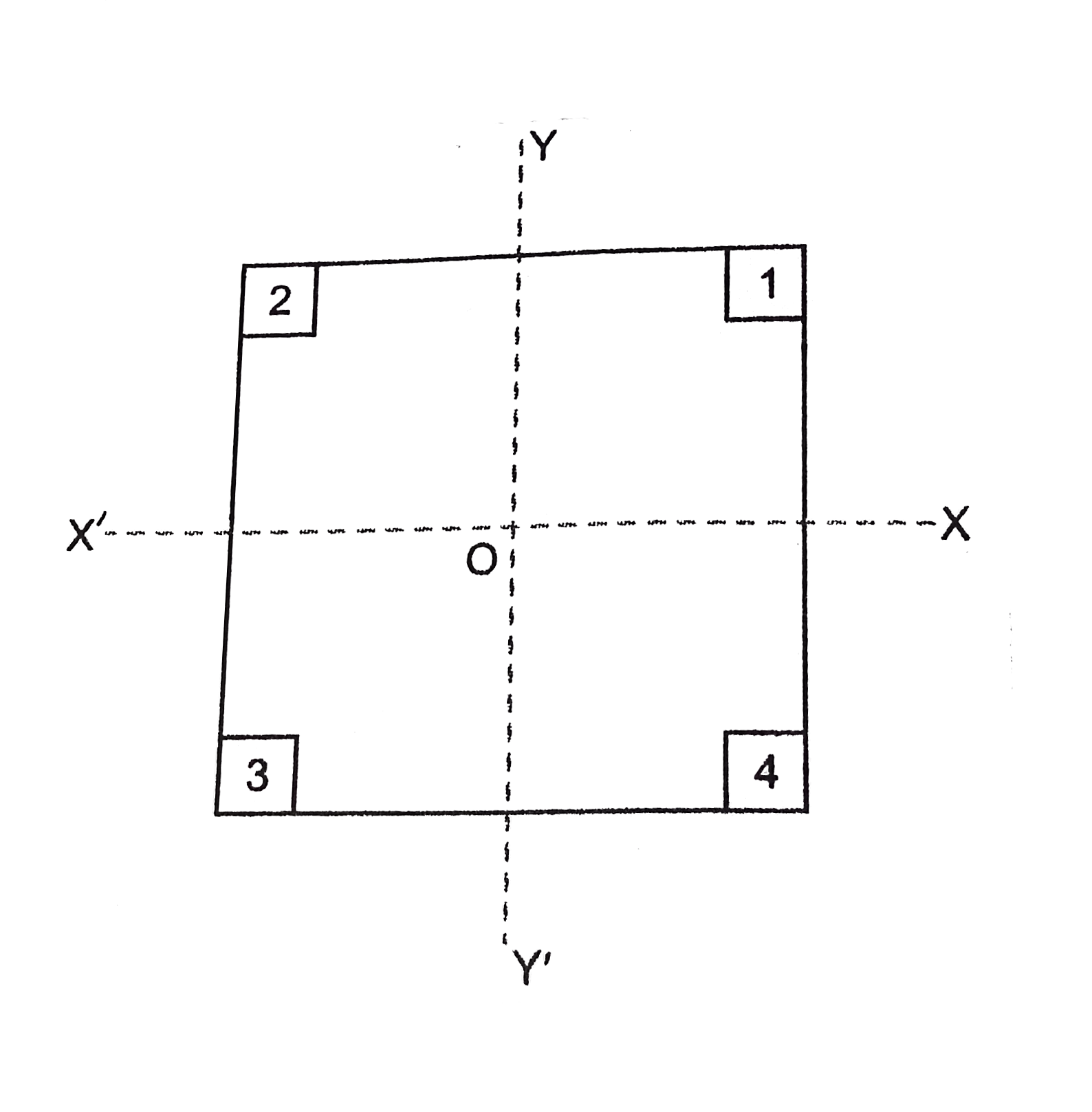
View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
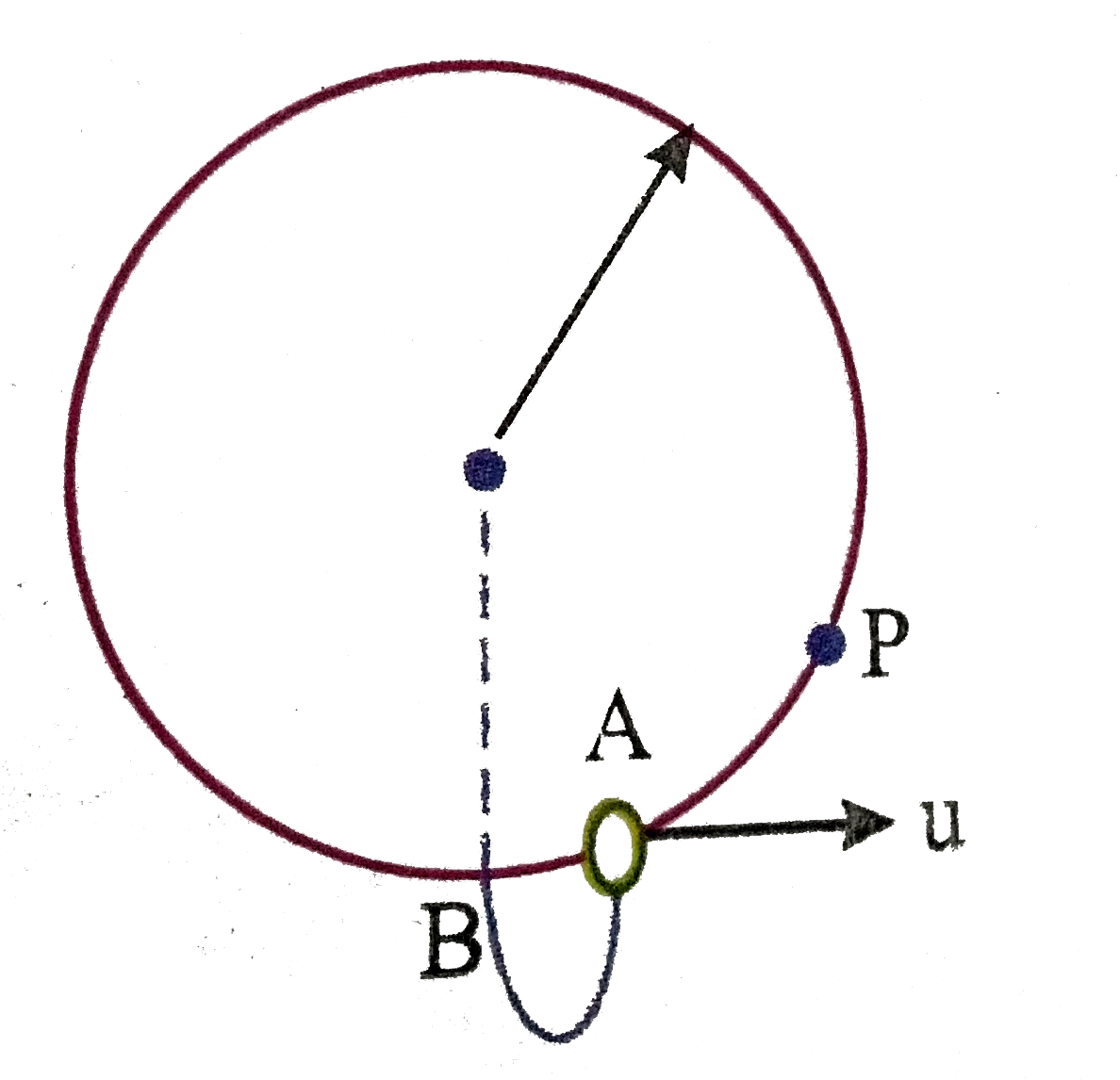
The smallest value u0 of u for which the bead will make complete revolutions of the wire will be
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
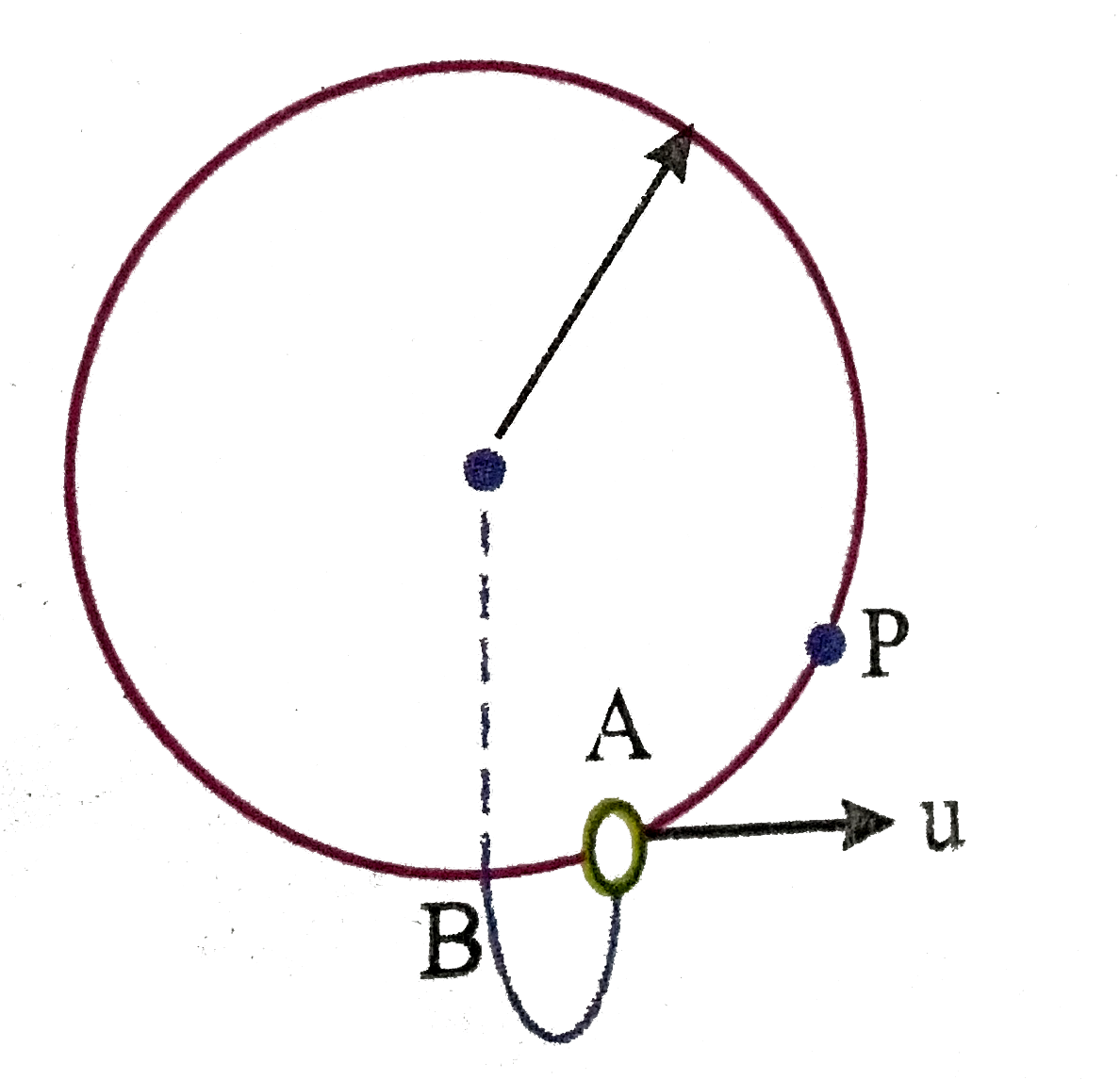
If v=2u0, the tension T in th elastic string when the bead is at the highest point B of the wire is
View SolutionA bead of mass m is threaded on a smooth circular wire centre O, radius a, which is fixed in vertical plane. A light string of natural olength 'a', elastic constant =3mga and breaking strength 3mg connects the bead to the lowest point A of the wire. The other end of the string is fixed to ring at point B near point A. The string is slaked initially. The bead is projected from A with speed u.
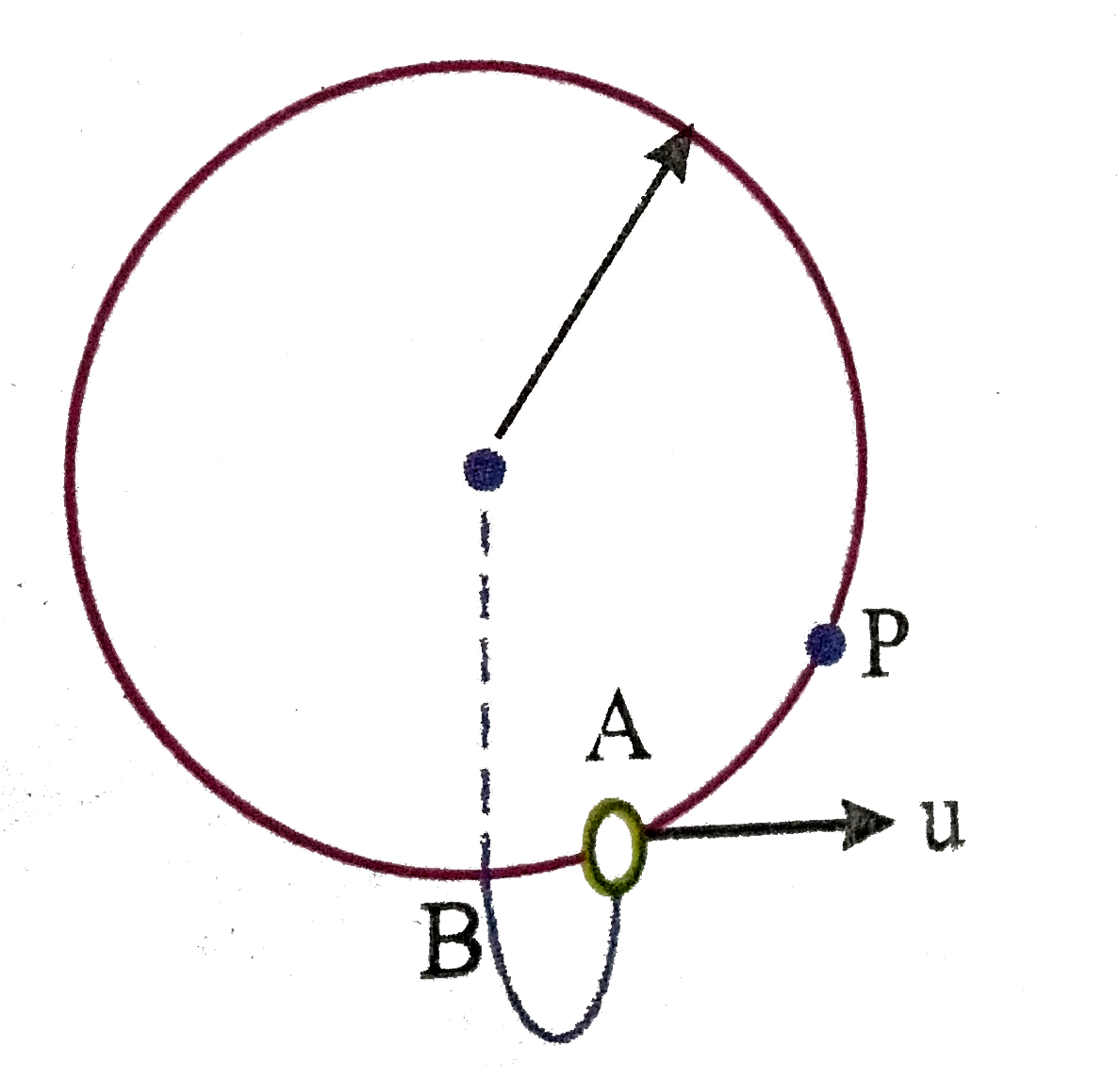
The elastic energy stored in the string when the bead is at the highest point B will be
View SolutionTwo beads of mass 2m and m , connected by a rod of length l and of negligible mass are free to move in a smooth vertical circular wire frame of radius l as shown. Initially the system is held in horizontal position ( Refer figure ) If the rod is replaced by a massless string of length l and the system is released when the string is horizontal then :
View SolutionA bead can slide on asmooth straight wire and a particle of mass m attached to the bead by a light string of length L. The particle is held in contact with the wire and with the string taut and is then let fall. If the bead has mass 2m then when the string makes an angle theta with the wire, the bead will have slipped a dsitance.
View SolutionThe Fig. showns a string of equally placed beads of mass m, separated by distance. The beads are free to slide without friction on a thin wire. A constant force F act on the first bead initially at rest till it makes collision with the second bead. The second bead then collides with the third and so on. Supposed that all collisions are elastic,
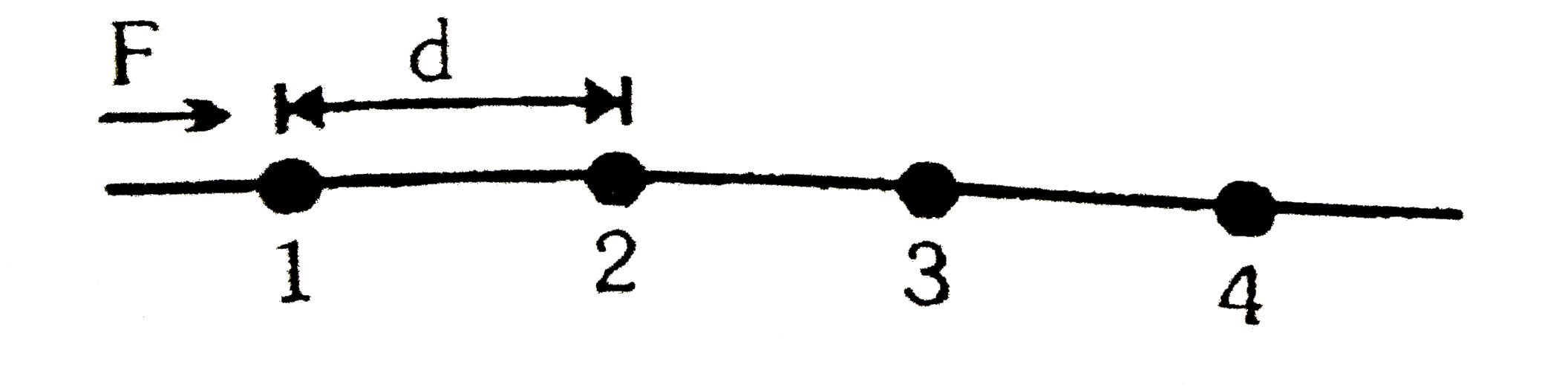
View SolutionA string of length '2a' has been tied at A and B such that AB='a' . The string is passing through a bead C and initially the bead is very close to A . Now the bead is allowed to fall. Let h be the height by which the bead falls when the string becomes taut and v be the speed of the bead just after the string becomes taut. Pick correct option (s):-
View SolutionIn the system shown in the figure , a bead of mass m can slide on the string. There is friction beween the bead and the string. Block B has mass equal to twice that of the bead. The system is released from rest with lenth l=18.75m of the string hanging below the bead. Assuming the pulley and string to be massless. Find the distance (in meter) moved by the block B before the bead slips out of the thread.
View SolutionIn the system shown in the fig., the bead of mass m can slide on the string. There is friction between the bead and the string. Block has mass equal to twice that of the bead. The system is released from rest with length l of the string hanging below the bead. Calculate the distance moved by the block before the bead slips out of the thread. Assume the string and pulley to be massless.
View SolutionStructures called beads on string are
View Solution
