Three particles starts from origin at the same time with a velocity along positive x-axis, the second with a velocity along negative y-axis, Find the velocity of the third particle along line so that the three particles may always lie in a straight line.Solution in Gujrati
The correct Answer is:B

co-ordinate of
Speed of 3rd particle
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-III
41 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV A
32 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-I
40 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
A particle of mass m, kinetic energy K and momentum p collision head on elastically with another particle of mass 2m at rest. After collision. :
Column IColumn II(A)Momentum of first particle(p)3/4p(B)Momentum of second particle(q)−K/9(C)Kinetic energy of first particle(r)−p/3(D)Kinetic energy of second particle(s)8K9None
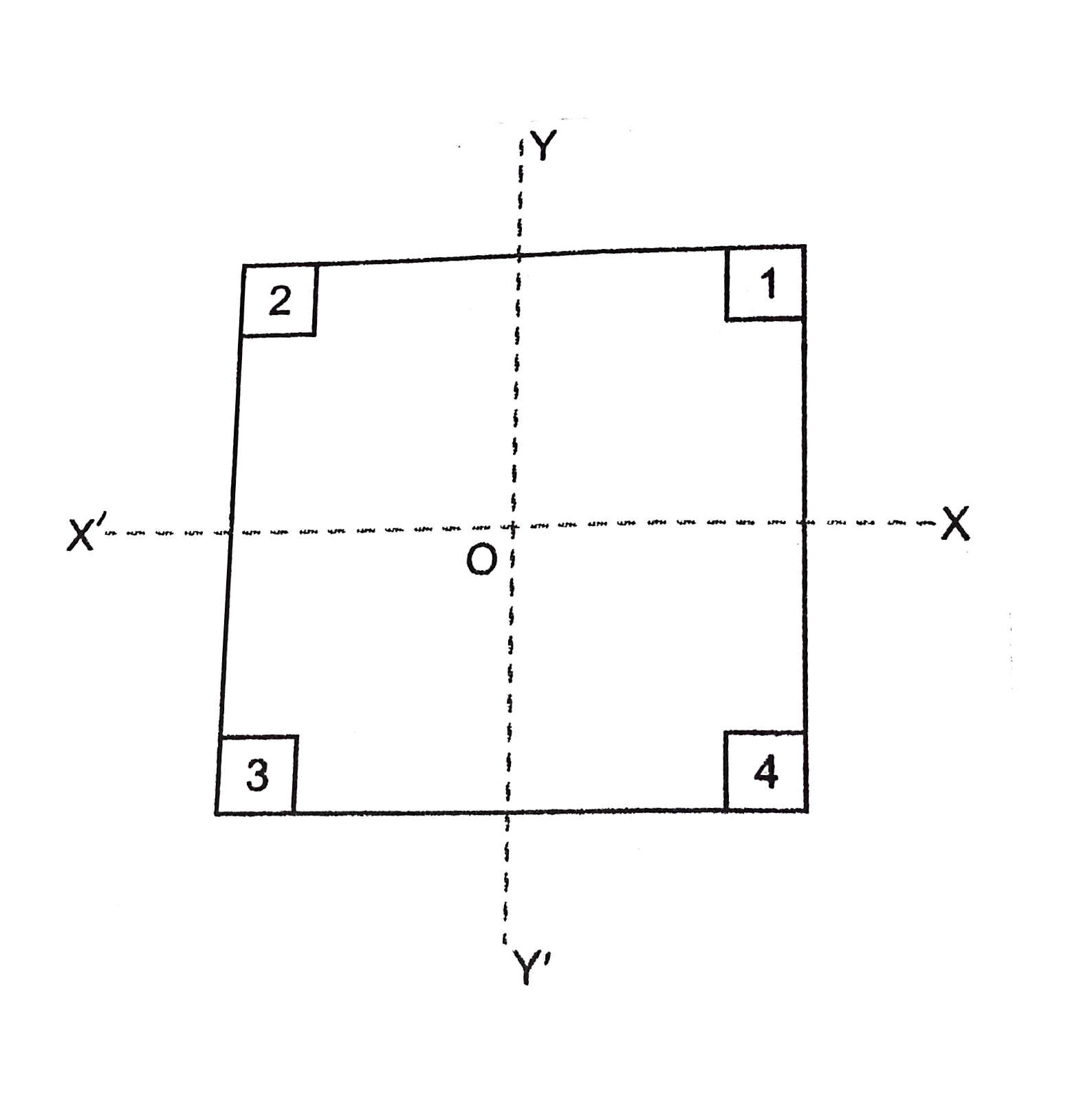
View SolutionFig. shown a uniform square plate from identical squares at the corners can be removed. (a) Where is the centre of mass of the plate originally ? (b) Where is it after square 1 is removed ?
(c ) where is it after squares 1 and 2 are removed ? (d) Where is c.m after squares 1,2,3, are removed ?
(f) Where is c.m after all the four squares are removed ? Answer in terms of quadrants and axes.
View SolutionThe centre of mass of a non uniform rod of length L whoose mass per unit length varies as p=kx2/L, (where k is a constant and x is the distance measured form one end) is at the following distances from the same end
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8 ms^(-1) at x = 0, then velocity of the particle at x = 1.4 m is (in ms^(-1)) .
View SolutionThree particles A,B and C start from the origin at the same time, A with a velocity a along x -axis, B with a velocity b along y -axis and C with velocity c in XY plane along the line x=y .The magnitude of c so that the three always remain collinear is:
View SolutionA particle is moving along a straight line along x-zxis with an initial velocity of 2m/s towards positive x-axis. A constant acceleration of 0.5m/s2 towards negative x-axis starts acting on particle at t=0. Find velocity (in m/s) of particle at t=2s.
View SolutionThree particles start from origin at the same time: one with velocity v^(1) along positive x-axis, the second along the positive y-axis with a velocity v^(2) and the third along the line y = x with such a speed that all the three always stay in a straight line, then velocity of the third particles is:
View SolutionThree particles start from the origin at the same time, one with velocity u1 along the x-axis, the second with velocity u2 along the y-axis . Find the velocity of the third particles, along the x=y line so that the three particles may always lie on the same straight line.
View SolutionThree particles start from the origin at the same time, one with a velocity v_(1) along the x-axis, second along the negative y-axis with a velocity v_(2) and third particle moves along the line x = y. The velocity of third particle, so that three may always lie on the same line is:
View SolutionThree particles A, B & C start from the origin at the same time, A with a velocity 'a' along x-axis, B with a velocity 'b' along y-axis and C with velocity 'c' in XY plane along the line x = y. The magnitude of 'c' so that the three always remain collinear is:
View SolutionThree particles A, B & C start from the origin at the same time, A with a velocity 'a' along X-axis, B with a velocity 'b' along y-axis and C with velocity 'c' in XY plane along the line x = y. The magnitude of 'c' so that the three always remain collinear is:
View SolutionThree particles A, B & C start from the origin at the same time, A with a velocity 'a' along X-axis, B with a velocity 'b' along y-axis and C with velocity 'c' in XY plane along the line x = y. The magnitude of 'c' so that the three always remain collinear is:
View SolutionThree particles start from origin at the same time: one with velocity v1 along positive x - axis, the second along the positive y-axis with a velocity v2 and the third along the line y=x with such a speed that all the three always stay in a straight line, then the velocity of the third particle is √kV1V2(V1+V2).
View SolutionThe acceleration of a particle which moves along the positive x-axis varies with its position as shown in figure. If the velocity of the particle is 0.8 ms^(-1) at x = 0, then velocity of the particle at x = 1.4 m is (in ms^(-1)) .
View Solution
