The block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is
 Solution in Gujrati
Solution in Gujrati
√MkL
kL22M
zero
ML2k
The correct Answer is:A
Let maximum momentum be p then
p22M=12kL2⇒p=L√Mk
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionThe block of mass M moving on the frictionless horizontal surface collides with the spring constant k and compresses it by length L . The maximum momention of the block after collision is

View SolutionA block of mass m is moving with a speed v on a horizontal rough surface and collides with a horizontal mounted spring of spring constant k as shown in the figure .The coefficient of friction between the block and the floor is μ The maximum compression of the spring is
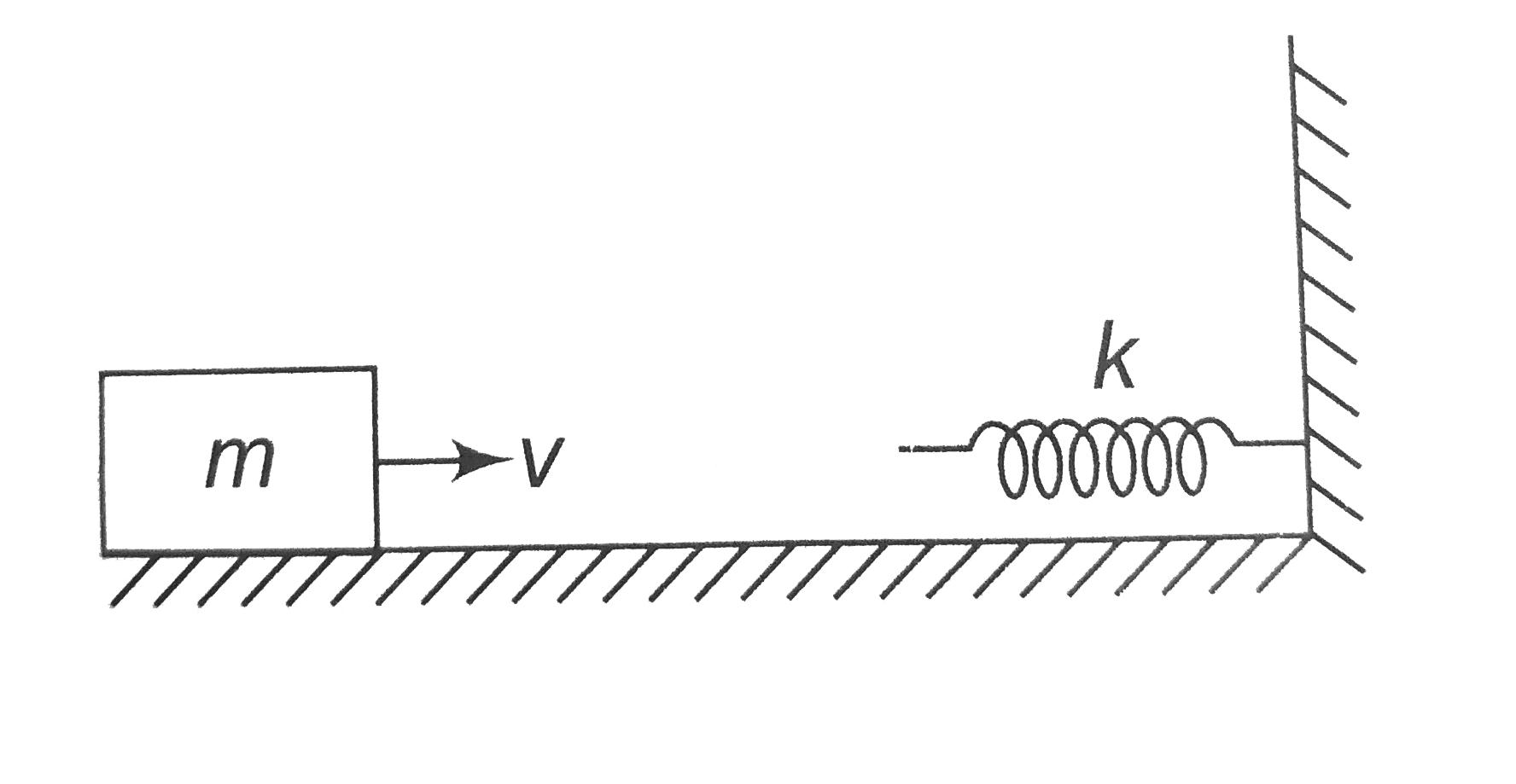
View SolutionA block of mass m moving at a speed v_0 compresses a spring of spring constant k as shown in the figure. Find (a) the maximum compression of spring and (b) speed of the block when the spring is compressed to half of maximum compression.
View Solutionचित्र में दो गुटके दिखाए गए हैं जिनके द्रव्यमान m तथा M है। ये गुटके एक घर्षणरहित क्षैतिज सतह पर रखे हैं तथा k स्प्रिंग नियतांक वाले एक स्प्रिंग से जुड़े हैं। प्रारंभ में स्प्रिंग अपनी स्वाभाविक लंबाई में है तथा गुटके स्थिर हैं। अब एक अचर बल F, द्रव्यमान M वाले गुटके पर लगना प्रारंभ करता है। स्प्रिंग की लंबाई में अधिकतम वृद्धि निकालें।
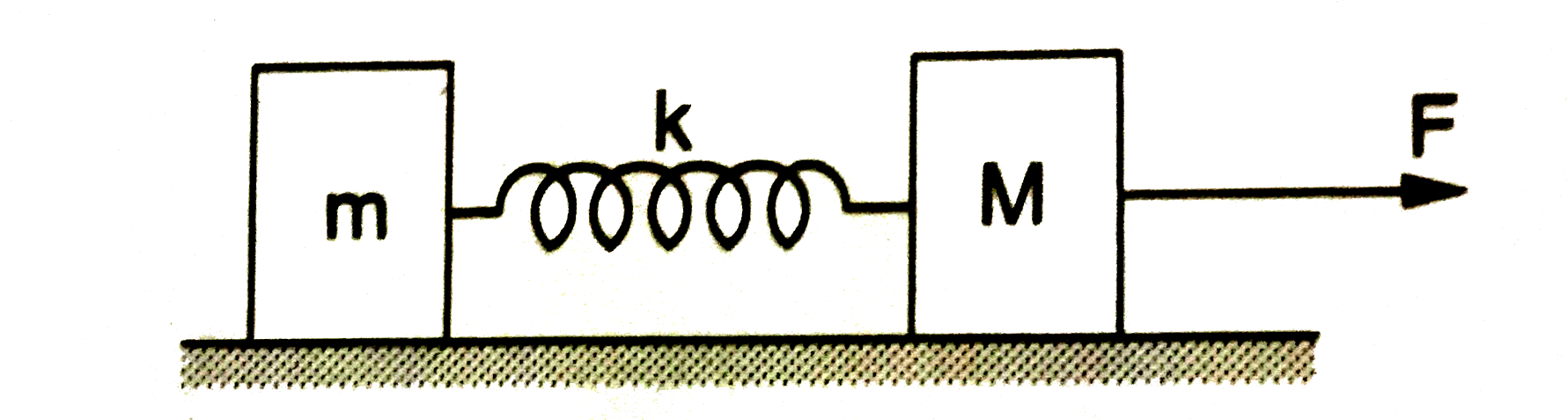
View SolutionA block of mass m is initially moving to the right on a horizontal frictionless surface at a speed v. It then compresses a spring of spring constant k. At the instant when the kinetic energy of the block is equal to the potential energy of the spring, the spring is compressed a distance of :
View Solution15 किग्रा का एक ब्लॉक 0.6 मी/से की चाल से एक घर्षणहीन मेज के क्षैतिज तल पर फिसलता है। यह ब्लॉक एक स्प्रिंग को संकुचित कर एक क्षण के लिए विरामावस्था में आ जाता है । स्प्रिंग में उत्पन्न अधिकतम संकुचन ज्ञात कीजिये। ( स्प्रिंग नियतांक k=1500 न्यूटन/ मी )
View SolutionA block of mass m moving with velocity v0 on a smooth horizontal surface hits the spring of constant k as shown. Two maximum compression in spring is
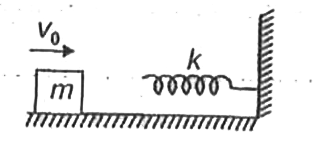
View SolutionA mass m moves with a speed v on a horizontal smooth surface and collides with a nearly massless spring whose spring constant is k. If the mass stops after collision, compute the maximum compression of the spring.
View SolutionA block of mass M moves on a frictionless horizontal surface to make k the segmental constant. The maximum momentum of the block will be after the collision
View Solutionm द्रव्यमान का एक गुटका v चाल से क्षैतिज खुरदुरी सतह पर गतिमान है तथा चित्रानुसार स्प्रिंग नियतांक k वाली क्षैतिज रूप से व्यवस्थित स्प्रिंग से टकराता है। गुटके एवं फर्श के मध्य का घर्षण गुणांकμ है। स्प्रिंग का अधिकतम संपीड़न होगा-

View SolutionM द्रव्यमान का एक गुटका जो घर्षणशील क्षैतिज सतह पर गति कर रहा है K स्प्रिंग नियतांक की एक स्प्रिंग से टकराता है तथा इसे L दूरी संपीडित करता है। संघट्ट के पश्चात गुटके का अधिकतम संवेग है-

View SolutionA block of mass .M. moving on the firctionless , horizontal surface collides with the spring of spring constant .k.. The other end of the spring is rigidly fixed to a vertical wall. If the spring is compressed by L, the maximum momentum of the block after collision is :
View Solution
