A thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as . Find the position of centre of mass of rod in meters. Solution in Gujrati
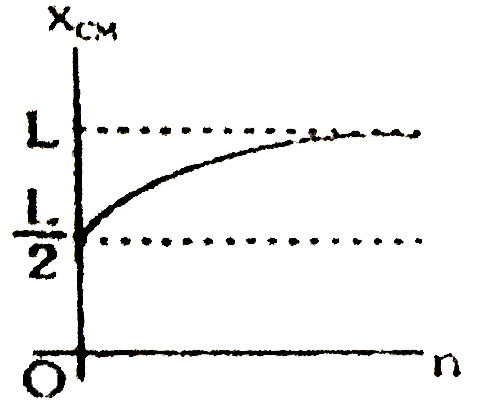

The correct Answer is:A
For and for
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L . The linear mass density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx . Here, a and b are constants. Find the position of centre of mass of this rod.
View SolutionA non-uniform thin rod of length L is palced along X-axis so that one of its ends is at the origin. The linear mass density of rod is lambda = lambda_(0)x . The centre of mass of rod divides the length of the rod in the ratio:
View SolutionA thin rod of length 6 m is lying along the x-axis with its ends at x=0 and x=6m. Its linear density *mass/length ) varies with x as kx4. Find the position of centre of mass of rod in meters.
View SolutionA thin rod of length 6m is lying along the x-axis with its ends at x=0 and x=6m. It linear density (mass/length) varies with x as kx4. Find the position of centre of mass of rod in meters.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/length) lamda of the rod varies with the distance x from the origin as lamda = Rx. Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA rod of length L is placed along the x-axis between x = 0 and x = L. The linear density (mass/ length) lambda of the rod varies with the distance x from the origin as lambda = Rx . Here, R is a positive constant. Find the position of centre of mass of this rod.
View SolutionA non–uniform thin rod of length L is placed along x-axis as such its one of ends at the origin. The linear mass density of rod is lambda=lambda_(0)x . The distance of centre of mass of rod from the origin is :
View SolutionA rod of length L is placed along the x -axis between x = 0 and x = L. The linear density (mass/length) ρ of the rod varies with the distance x from the origin as ρ=a+bx . Here a and b are constants. Find the position of centre of mass of this rod.

View SolutionIf the linear density of a rod of length L varies as λ=A+Bx, find the position of its centre of mass.
View SolutionIf the linear density of a rod of length L varies as lambda=A+Bx , find the position of its centre of mass.
View SolutionLinear mass density of a rod AB ( of length 10 m) varied with distance x from its end A as lambda = lambda_0 x^3 ( lamda_0 is positive constant). Distance of centre of mass the rod, form end B is
View SolutionA rod of length L is placed along the x-axis between x=0 and x=L . The linear mass density (mass/length) rho of the rod varies with the distance x from the origin as rho=a+bx . Here, a and b are constants. Find the position of centre of mass of this rod.
View Solution
