A mass 'm' moves with a velocity 'v' and collides inelastieally with another identical mass . After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the 2nd mass after collision.
⋅→mbeforecollision⋅m↑⏐
⏐
⏐
⏐⏐v/√3aftercollision⟩Solution in Gujrati
v
√3v
2√3v
vsqer3
The correct Answer is:C
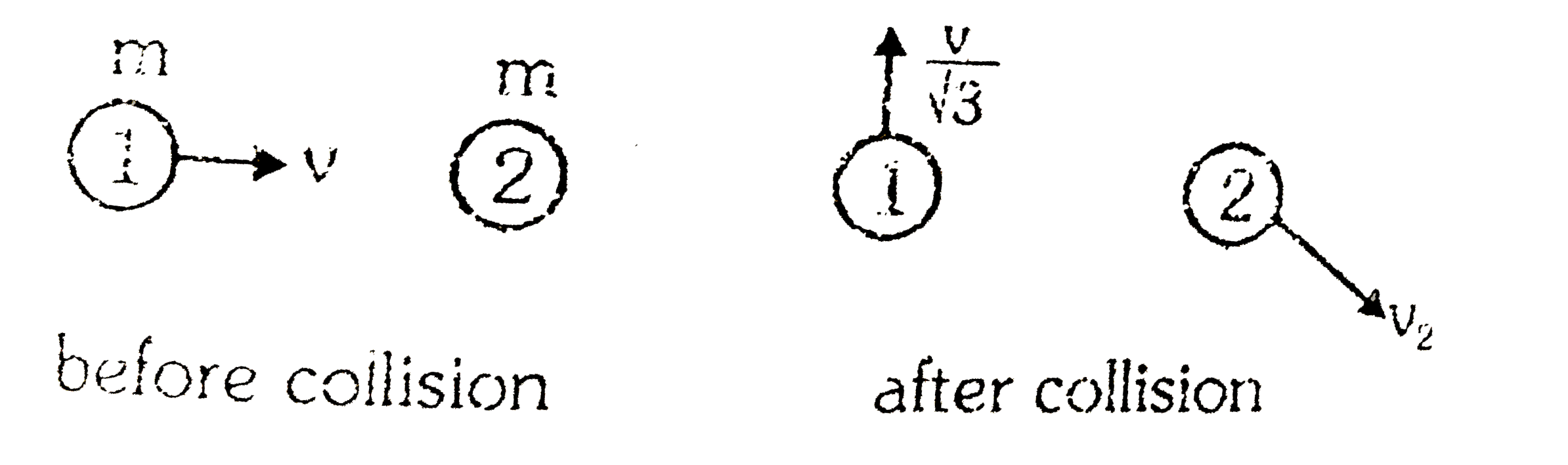
From COLM
mv2=
⎷(mv2)+(mv√3)2⇒v2=2v√3
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V B
19 Videos
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-IV B
14 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣
View SolutionA bullet of mass M is fired with a velocity 50m/s at an angle with the horizontal. At the highest point of its trajectory, it collides head-on with a bob of mass 3M suspended by a massless string of length 10/3 metres and gets embeded in the bob. After the collision, the string moves through an angle of 120∘. Find
(i) the angle θ,
(ii) the vertical and horizontal coordinates of the initial position of the bob with respect to the point of firing of the bullet. Take g=10m/s2
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View SolutionA ball of mass M moving with a velocity v collides perfectly inelastically with another ball of same mass but moving with a velocity v in the opposite direction. After collision
View SolutionA ball of mass m moving with a velocity v undergoes an oblique elastic collision with another ball of the same mass m but at rest. After the collision if the two balls move with the same speeds , the angle between their directions of motion will be:
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass. After collision the 1st mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision
View SolutionA mass ‘m’ moves with a velocity ‘v’ and collides inelastically with another identical mass at rest. After collision the 1st mass moves with velocity (v)/(sqrt(3)) in a direction perpendicular to the initial direction of motion. Find the speed of the 2^(nd) mass after collision :
View SolutionA sphere of mass m moves with a velocity 2v and collides inelastically with another identical sphere of mass m. After collision the first mass moves with velocity v in a direction perpendicular to the initial direction of motion . Find the speed of the second sphere after collision .
View SolutionA sphere of mass M moving with velocity w collides elastically with another of mass m at rest. After collision their final velocities are V and v. The value of vis:
View SolutionA mass 'm' moves with a velocity '' and collides inelastically with another identical mass. After collision the Ist mass moves with velocity in a direction perpen-dicular to the initial direction of motion Find the speed of the 2nd mass after collision :
View SolutionA sphere of mass M moving with velocity u collides elastically with another of mass mat rest. After collision their final velocities are V and v. The value of v is:
View SolutionA mass m moves with a velocity .y. and collides inelastically with another identical mass. After collision the first mass moves with velocity v√3 in a direction perpendicular to the initial direction of motion. What is the speed of second mass after collision ?

View SolutionA particle of mass m moving with velocity v is collide with a stationary particle of mass 2 m . The speed of the system , after collision will be ……….
View SolutionA mass m moves with a velocity v and collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity v/(sqrt3) in a direction perpendicular to Before collision the initial direction of motion. The speed of the 2^(nd) mass after collision
View SolutionWhen is a collision said to be a perfectly inelastic? A mass is moving with speed v collides inelastically with another identical mass at rest. After collision, the first mass moves with velocity ν√3 in a direction perpendicular to the initial direction of motion. Find the speed of the second mass after collision.
View Solution
