Consider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
Column-IColumn-IIColumn-III(I)Maximum speed of the ring is v(i)Minimum speed of the particle isv/2(P)Final speed of the ring and particle is v and zero respectively.(II)Maximum speed of the ring isv/2(ii)Minimum speed of the particle is zero(Q)Final speed of the ring and particle is zero and v respectively.(III)Maximum speed of the ring isv2[1+√1−Qqπε0mrv2](iii)Minimum speed of the particle isv2[1+√1−Qqπε0mrv2](R)Final speed of the ring and particle is v/4 and3v/4 respectively.(IV)Maximum speed of the ring isv2[1−√1−Qqπε0mrv2](iv)Minimum speed of the particle isv2[1−√1−Qqπε0mrv2](S)Final speed of the ring and particle is v/2 for both.
Which of following options is the correct representation if v=√2Qqπε0mr
(II)(i)S
(I)(ii)P
(III)(iv)Q
(IV)(iii)(Q)
The correct Answer is:D
Let v be the velocity of particle for which both moves together finally
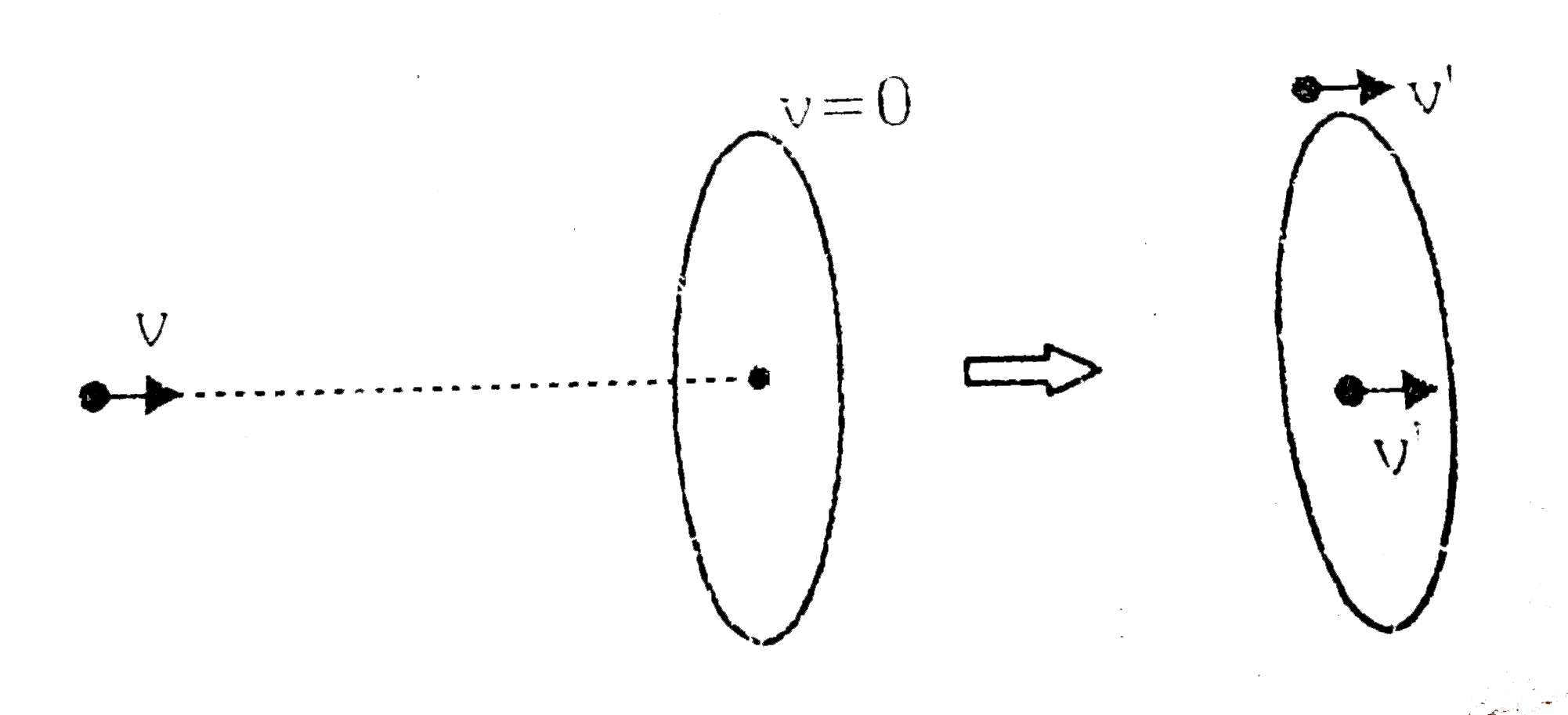
pi=pf
mv=2mv′⇒v′=v2….(i)
Ei=Ef
12mv2(12mv'2)×2−kQqr.....(ii)
v=√Qqπε0mr
If v<√Qqπε0mr then velocity of particle continously decrease and that of ring continously increase. Final velocity of particle becomes zero and that of ring becomes v
If v>√Qqπε0mr then particle crosses the ring and again it's velocity start increasing and finally becomes v and that of ring becomes zero.
pi=pf⇒mv=mv1+mv2....(i)
12mv2=12mv21+12mv22+kQqr....(ii)
Minimum speed of particle
v1=v2[1+√1−Qqπε0mrv2]

Maximum speed of ring
v2=v2[1−√1−Qqπεmv2]
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physic
48 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PHYSICS
16 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
Consider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
Column-IColumn-IIColumn-III(I)Maximum speed of the ring is v(i)Minimum speed of the particle isv/2(P)Final speed of the ring and particle is v and zero respectively.(II)Maximum speed of the ring isv/2(ii)Minimum speed of the particle is zero(Q)Final speed of the ring and particle is zero and v respectively.(III)Maximum speed of the ring isv2[1+√1−Qqπε0mrv2](iii)Minimum speed of the particle isv2[1+√1−Qqπε0mrv2](R)Final speed of the ring and particle is v/4 and3v/4 respectively.(IV)Maximum speed of the ring isv2[1−√1−Qqπε0mrv2](iv)Minimum speed of the particle isv2[1−√1−Qqπε0mrv2](S)Final speed of the ring and particle is v/2 for both.
Which of following options is the correct is the representation ifv=√Qq2πε0mr
View SolutionElectric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View Solution
Knowledge Check
Consider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
Column-IColumn-IIColumn-III(I)Maximum speed of the ring is v(i)Minimum speed of the particle isv/2(P)Final speed of the ring and particle is v and zero respectively.(II)Maximum speed of the ring isv/2(ii)Minimum speed of the particle is zero(Q)Final speed of the ring and particle is zero and v respectively.(III)Maximum speed of the ring isv2[1+√1−Qqπε0mrv2](iii)Minimum speed of the particle isv2[1+√1−Qqπε0mrv2](R)Final speed of the ring and particle is v/4 and3v/4 respectively.(IV)Maximum speed of the ring isv2[1−√1−Qqπε0mrv2](iv)Minimum speed of the particle isv2[1−√1−Qqπε0mrv2](S)Final speed of the ring and particle is v/2 for both.
Which of following options is the correct is the representation ifv=√Qq2πε0mrA(II)(i)SB(I)(ii)PC(III)(iv)RD(IV)(iii)QConsider a non conduting ring of radius r and mass m and a particle of same mass, both at rest in free space. The particle is on the axis of the ring and far away from the ring. An amount Q of positive charge is uniformly distributed on the ring and the particle is given a positive charge q. The particle is imparted a velocity v towards the centre of the ring. Consider the consequences given in the columns and answer the following question
Column-IColumn-IIColumn-III(I)Maximum speed of the ring is v(i)Minimum speed of the particle isv/2(P)Final speed of the ring and particle is v and zero respectively.(II)Maximum speed of the ring isv/2(ii)Minimum speed of the particle is zero(Q)Final speed of the ring and particle is zero and v respectively.(III)Maximum speed of the ring isv2[1+√1−Qqπε0mrv2](iii)Minimum speed of the particle isv2[1+√1−Qqπε0mrv2](R)Final speed of the ring and particle is v/4 and3v/4 respectively.(IV)Maximum speed of the ring isv2[1−√1−Qqπε0mrv2](iv)Minimum speed of the particle isv2[1−√1−Qqπε0mrv2](S)Final speed of the ring and particle is v/2 for both.
Which of following options is the correct is the representation ifv=√Qqπε0mrA(II)(i)SB(I)(ii)PC(III)(iv)RD(IV)(iii)QCharges q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
Aq2π2ε0R2Bq4π2ε0R2Cq4πε0R2Dq2πε0R2
Electric charge Q is uniformly distributed around a thin ring of radius a. find the potential a point P on the axis of the ring at a distance x from the centre of the ring .

View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring.

View SolutionCharge q is uniformly distributed over a thin half ring of radius R. The electric field at the centre of the ring is
View SolutionCalculate potential on the axis of a ring due to charge Q uniformly distributed along the ring of radius R.
View SolutionA positive charge Q is uniformly distributed along a circular ring of radius R.a small test charge q is placed at the centre of the ring .The

View Solution
