Consider a finite charged rod. Electric field at point P (shown) makes an angle θ with horizontal dotted line then angle θ is:-
 Solution in Gujrati
Solution in Gujrati
60∘
28∘
44∘
information insufficient
The correct Answer is:B
Required angle=θ2−θ12=88∘−32∘2=56∘2=28∘
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Part -II Example Some worked out Examples
1 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Exercise-01
87 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - Question
1 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
For spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is →E=kr7→r, where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?
View SolutionA stone is dropped into a quiet lake and waves move in circles speading out radially at the speed of 5 cm/s. At the instant when the radius of the circular wave is 8cm, how fast is the enclosed area increasing?
View SolutionA simple pendulum of length l and bob mass m is hanging in front of a large nonconducting sheet having surface charge density σ. If suddenly a charge +q is given to the bob & it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
 .
.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA spool is pulled at an angle theta with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle theta is equal to
View SolutionA pendulum bob of mass m charge q is at rest with its string making an angle θ with the vertical in a uniform horizontal electric field E. The tension in the string in
View SolutionThe direction (θ) of →E at point P due to uniformly charged finite rod will be

View SolutionAn electric field line emerges from a positive point charge +q at angle alpha to the straight line connecting it to a negative point charge -2q as shown in figure. At what angle beta with the field line enter the charge -2q ?
View SolutionTwo charges +Q " and " -2Q are located at points A and B on a horizontal line as shown below The electric field is zero at a point which is located at a finite distance
View SolutionA mirror is inclined at an angle of theta with the horizontal. If a ray light is incident at an angle theta as shown , then the angle made by reflected ray with the horizontal is
View Solutionमूलबिन्दु O पर X-अक्ष के अनुदिश एक विद्युत् द्विध्रुव रखा गया है इस मूल बिन्दु से 20 सेमी दूर एक ऐसा बिन्दु P स्थित है कि रेखा OP, X-अक्ष से कोण (π)/3 बनाती है। यदि बिन्दु P पर विद्युत् क्षेत्र, X-अक्ष के साथ कोण θ बनाता है, तो θ का मान होगा :
View SolutionA point mass is projected, making an acute angle with the horizontal. If angle between velocity →v and acceleration →g is θ, then θ is given by
View SolutionTwo projectiles A and B are thrown with the same speed such that A makes angle θ with the horizontal and B makes angle θ with the vertical, then -
View SolutionA rod of mass m is released on smooth horizontal surface making angle theta with horizontal. Then which of the following statement is correct ?
View Solution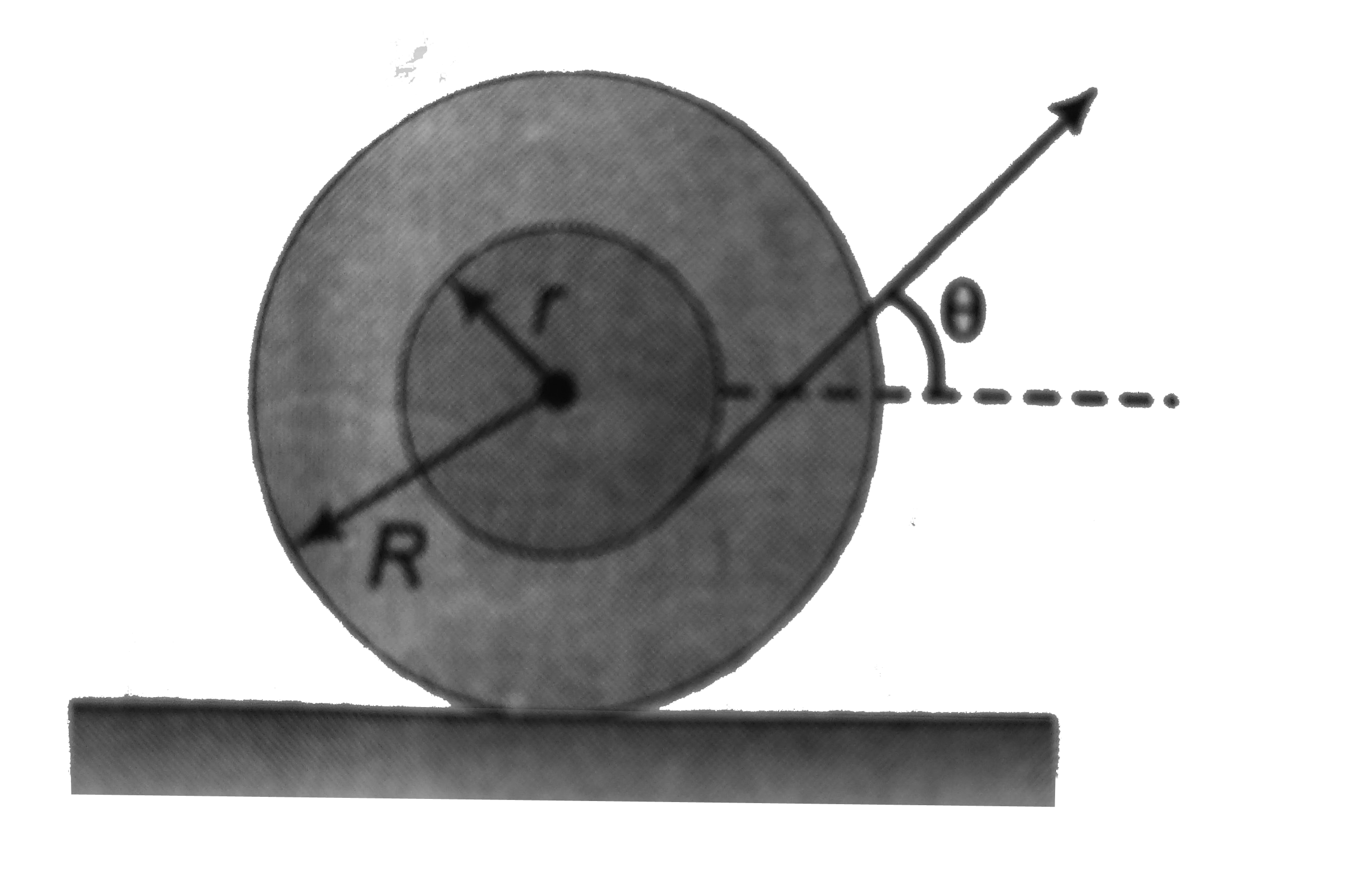
A spool is pulled at an angle θ with the horizontal on a rough horizontal surface as shown in the figure. If the spool remains at rest, the angle θ is equal to
View Solution
