[Gujrati] A thin homogeneous rod of mass m and length l is free to rot

For spherically symmetrical charge distribution, electric field at a distance r from the centre of sphere is $\to E = k r^{7} \to r$ , where k is a constant. What will be the volume charge density at a distance r from the centre of sphere?

View Solution

A stone is dropped into a quiet lake and waves move in circles speading out radially at the speed of $5$ $c m / s$ . At the instant when the radius of the circular wave is $8 c m$ , how fast is the enclosed area increasing?

View Solution

A simple pendulum of length $l$ and bob mass $m$ is hanging in front of a large nonconducting sheet having surface charge density $σ$ . If suddenly a charge $+ q$ is given to the bob $&$ it is released from the position shown in figure. Find the maximum angle through which the string is deflected from vertical .
ocr_image .

View Solution

A football player kicks a ball at an angle of $30^{\circ}$ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, $(g = 10 m / s^{2})$

View Solution

Assertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.

View Solution

ocr_image
A uniform rod of length $L$ and mass $m$ is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass $m$ is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is

View Solution

A uniform thin rod of length l and mass m is hinged at a distance l//4 from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is

View Solution

Consider a rod of mass $M$ and length $L$ pivoted at its centre is free to rotate in a vertical position plane. The rod is at rest in the vertical position. A bullet of mass $M$ moving horizontally at a speed $v$ strikes and embedded in one end of the rod. The angular velocity of the rod just after the collision will be.

View Solution

A uniform rod of length $L$ and mass $M$ is free to rotate about a frictionless pivot at one end. The rod is released from rest in the horizontal position. What are the initial angular acceleration of the rod and the initial linear acceleration of the right end of the Rod ?
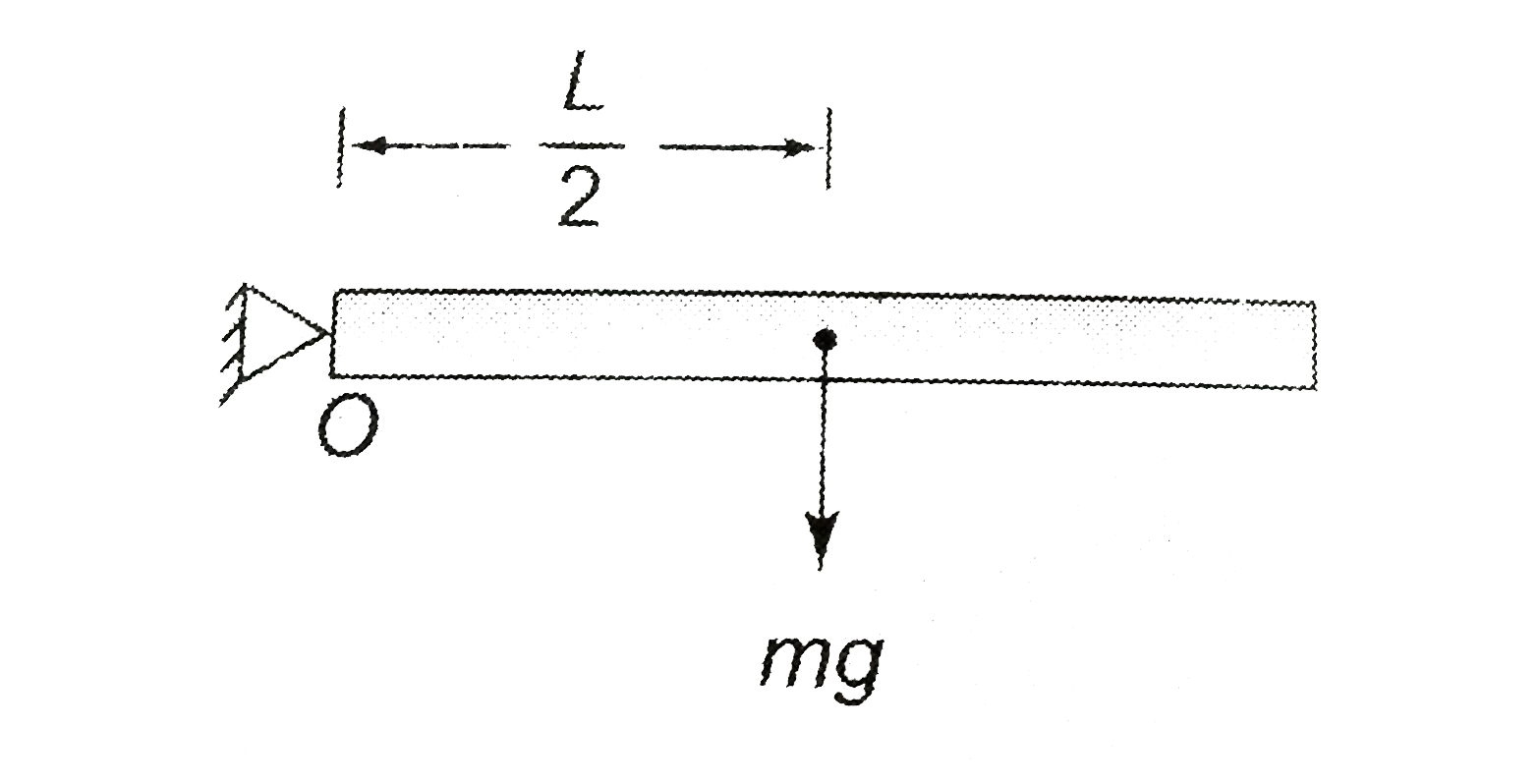
ocr_image

View Solution

A thin uniform rod of length l and mass m is freely pivoted about its end. The rod is initially held horizontally and released from rest. When the rod is vertical, an impulse J is applied to bring it to rest (this is in addition to any impulse provided by the pivot) What is the angular velocity of the rod at the moment it reaches the vertical position ?

View Solution

AB is a mass less rigid rod of length 2l. It is free to rotate in vertical plane about a horizontal axis passing through its end A. Equal point masses (m each) are stuck at the centre C and end Bof the rod. The rod is released from horizontal position. Write the tension in the rod when it becomes vertical.

View Solution

A thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=(mg)/(2q) . The rod is released from, shown position from rest. What is the angular acceleration of the rod at the instant of releasing the rod?

View Solution

A thin homogeneous rod of mass m and length l is free to rotate in vertical plane about a horizontal axle pivoted at one end of the rod. A small ballof mass m and charge q is attached to the opposite end of this rod. The whole system is positioned in a horizontal electric field of magnitude E=(mg)/(2q) . The rod is released from, shown position from rest. What is the acceleration of the small ball at the instant of releasing the rod?

View Solution

A rod of length l is released from the vertical position on a smooth horizontal plane. What is the nature of motion of the free end of the rod ?

View Solution

ocr_image
A uniform rod of length $L$ and mass $m$ is free to rotate about a frictionless pivot at one end as shown in figure. The rod is held at rest in the horizontal position and a coin of mass $m$ is placed at the free end. Now the rod is released The reaction on the coin immediately after the rod starts falling is

View Solution

A uniform thin rod of length $l$ and mass $m$ is hinged at a distance $l / 4$ from one of the end and released from horizontal position as shown in Fig. The angular velocity of the rod as it passes the vertical position is
ocr_image

View Solution

The correct Answer is:C

From work energy theorem $\frac{1}{2} I ω^{2} = m g (\frac{l}{2}) + m g l - q E l$
$\frac{1}{2} (\frac{4}{3} m l^{2}) ω^{2} = \frac{3}{2} m g l - \frac{m g l}{2} \Rightarrow \frac{2}{3} m l^{2} ω^{2} = m g l \Rightarrow ω = \sqrt{\frac{3 g}{2 l}}$
Speed of ball $= ω l = \sqrt{\frac{3 g l}{2}}$

Topper's Solved these Questions

Similar Questions

ALLEN -MISCELLANEOUS-Part -II Example

The correct Answer is:C

From work energy theorem 12Iω2=mg(l2)+mgl−qEl 12(43ml2)ω2=32mgl−mgl2⇒23ml2ω2=mgl⇒ω=√3g2l Speed of ball =ωl=√3gl2

Topper's Solved these Questions

Similar Questions

ALLEN -MISCELLANEOUS-Part -II Example

From work energy theorem $\frac{1}{2} I ω^{2} = m g (\frac{l}{2}) + m g l - q E l$
$\frac{1}{2} (\frac{4}{3} m l^{2}) ω^{2} = \frac{3}{2} m g l - \frac{m g l}{2} \Rightarrow \frac{2}{3} m l^{2} ω^{2} = m g l \Rightarrow ω = \sqrt{\frac{3 g}{2 l}}$
Speed of ball $= ω l = \sqrt{\frac{3 g l}{2}}$