A conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?Solution in Gujrati
The correct Answer is:(i) Un=q2n8π∈0R (ii) U∞=Q2R8π∈0r2 Here qn=QRr[1−(RR+r)n]
Capacities of conducting spheres are in the ratio of their radii. Let C1 and C2 be the capacities of S1 and S2, then C2C1=Rr
(i) Charges are distributed in the ratio of their capacities. Let in the first constant, charge acquired by S2, is q1,. Therefore, charge on S1 will be Q−q.
Say it is q'1∴q1q'1=q1Q−q1=C2C1=Rr
It implies that Q charge is to be distributed in S2 and S1 in the ratio of R/r.
∴q1=Q(RR+r)...(i)
In the second contact, S1 again acquires the same charge Q. Therefore, total charge in S1 and S2 will
Q+q1=Q(1+RR+r)
This charge is again distributed in the same ratio. therefore, charge on S2 in second contact,
q1=Q(1+RR+r)(RR+r)=Q[RR+r+(RR+r)2]
similarly,
q3=Q[RR+r+(RR+r)2+(RR+r)3] and
qn=Q[RR+r+(RR+r)2+...+(RR+r)n]
⇒qn=QRr[1−(RR+r)n]...(i) [Sn=a(1−rn)(1−r)]
Therefore, electrostatic energy of S2 after n such contacts
Un=q2n2C=q2n2(4πε0R)⇒Un=q2n8πε0R
where qn can be written from Eq. (2)
(ii) qn=QRR+r[1+RR+r+...+...+(RR+r)n−1]
as n→∞
q∞=QRR+r⎛⎜⎝11−RR+r⎞⎟⎠=QRR+r(R+rr)=QRr
[S∞=a1−r]
∴U∞=q2∞2C=Q2R2/r28πε0R⇒U∞=Q2R8πε0r2
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - PHY
68 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-1
121 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - LINKED COMPREHENSION TYPE
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Find roots equation 2x2−x−3=0.
View SolutionIf the vectors →a,→b,and→c form the sidesBC,CAandAB, respectively, of triangle ABC,then
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
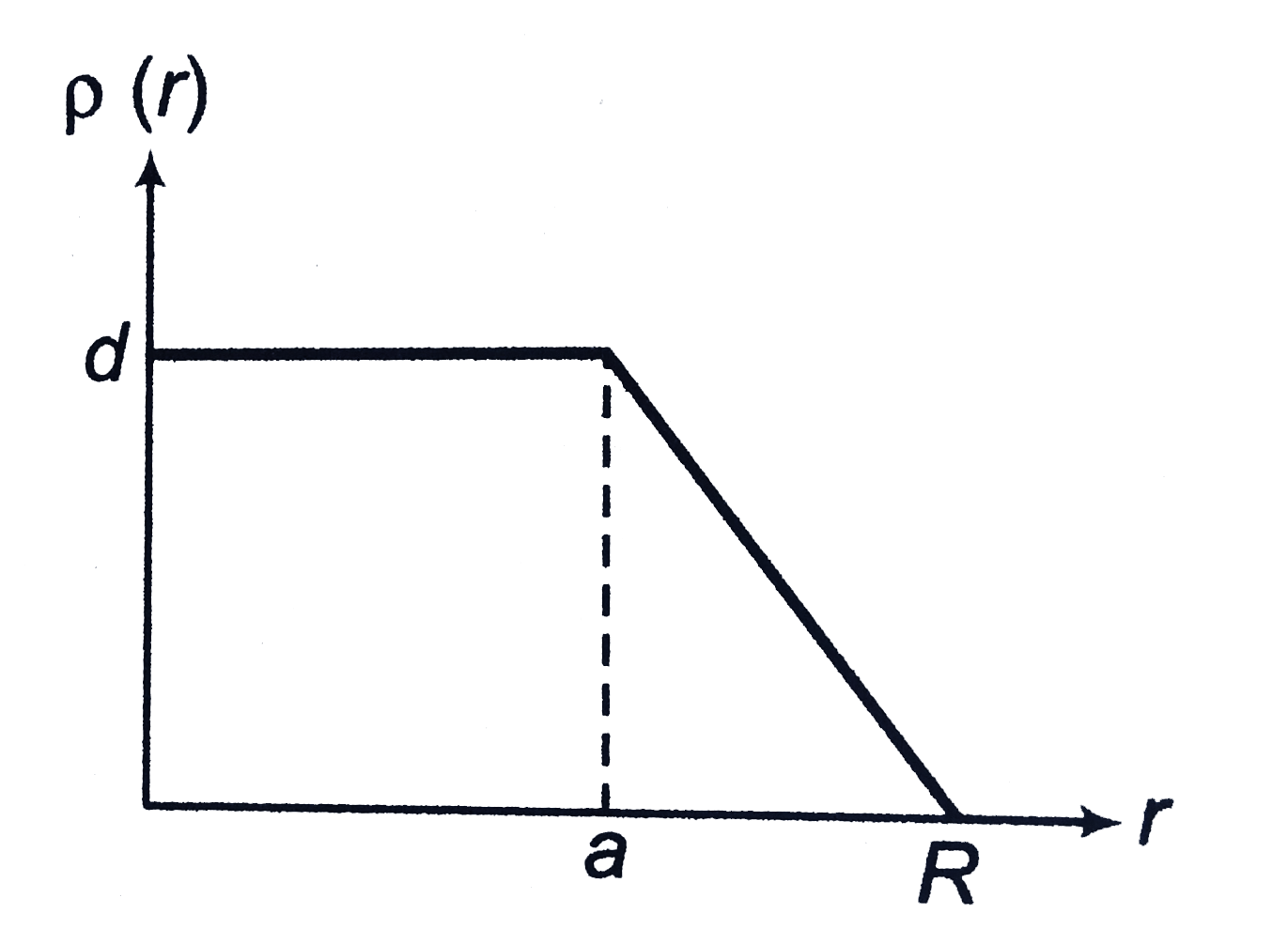
The electric field at r=R is
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA conducting shell S1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S2. Let the potential difference between S1 and that S2 be V. If the shell S2 is now given a charge −3Q, the new potential difference between the same two shells is
View SolutionA conducting sphere S1 of radius r is attached to an insulating handle. Another conduction sphere S2 of radius R is mounted on an insulating stand. S2 is initially uncharged. S1 is given a charge Q brought into contact with S2 and removed. S1 is recharge such that the charge on it is again Q and it is again brought into contact with S2 and removed. This procedure is repeated n times.
a. Find the electrostatic energy of S2 after n such contacts with S1.
b. What is the limiting value of this energy as n→∞ ?
View SolutionConsider two concentric spherical surfaces S_1 with radius a and S_2 with radius 2a, both centered at the origin. There is a charge +q at the origin and there are no other charges. Compare the flux phi_1 through S_1 with the flux phi_2 through S_2 .
View SolutionConsider a solid neutral conducting sphere S_(1) of radius r=3.0m. A point charge Q=+2muC s placed at point P such that AP=-4.0m (AP is tangent to the sphere). Charge Q' is induced on the surface of te conducting sphere S_(1) . Consider another non conducting sphere (S_(2)) of same radius r. Charge Q' is spread on the surfaec of S_(2) in exactly the same way as it is present on the surface of conducting sphere S_1 [i.e., the distribution of charge on surface of S_2 is exact replica of the induced surface charge on S_1 ]. There is no other charge in vicinity of S_2 . Find the smallest potential (at a point) on the surface of sphere S_2 .
View SolutionTwo isolated conducting spheres S1andS2 of radius 23Rand13R have 12μC and −3μC charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire . A long time after this is done the charges on S1andS2 are respectively :
View SolutionA thick hollow metallic sphere of Inner and outer radius 2a and 4a, respectively, encloses a sold concentric metallic sphere of radius a'. These spheres are connected to the earth through switches S_1 and S_2 as shown in the figure First, switch S_1 is closed and after some time S_1 is opened. Then, S_2 is closed and after some time S_2 is opened. This completes one cycle. Initially, charge Q is given to the outer sphere with both S_1 and S_2 open. The charge on the inner sphere after n cycles of earthing the inner and outer spheres is
View SolutionA sphere S_1 of radius r enclose a total charge Q. If there is another concentric sphere S_2 of radius r_2 (gtr_1) and there be no additioanl charges between S_1 and S_2 find the ratio of electric flux through S_1 and S_2
View SolutionTwo isolated conducting spheres S_1 and S_2 of radius 2/3 R and 1/3 R have 12 mu C and -3 muC charges, respectively, and are at a large distance from each other. They are now connected by a conducting wire . A long time after this is done the charges on S_1 and S_2 are respectively :
View SolutionA conducting sphere A of radius r is attached on an insulating hand. Another sphere B of radius.R.is mounted on an insulating stand. Initially A is given a charge Q, it is bought in contact with B and removed. A is charged to O afer each contact. This process is repeated ni times Match the Column I with Column II and choose the correct option code.

View SolutionA conducting shell S_1 having a charge Q is surrounded by an uncharged concentric conducting spherical shell S_2 . Let the potential difference between S_1 and that S_2 be V. If the shell S_2 is now given a charge -3Q , the new potential difference between the same two shells is
View Solution
