A solid sphere of radius R has a charge Q distributed in its volume with a charge density ρ=kra, where k and a are constants and r is the distance from its centre. If the electric field at r=R2 is 18 times that r=R, find the value of a.Solution in Gujrati
The correct Answer is:2
E(4πr2)=∫(kra)4πr2dr∈0
E(r2)=∫ra+2dr∈0
⇒E(r2)=ra+3(a+3)∈0⇒E=ra+1(a+3)∈0
⇒E(R/2)=E18E(R)⇒(R2)a+1=18(R)
⇒2a+1=23⇒a=2

Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - PHY
68 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-1
121 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - LINKED COMPREHENSION TYPE
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Find roots equation 2x2−x−3=0.
View SolutionIf the vectors →a,→b,and→c form the sidesBC,CAandAB, respectively, of triangle ABC,then
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
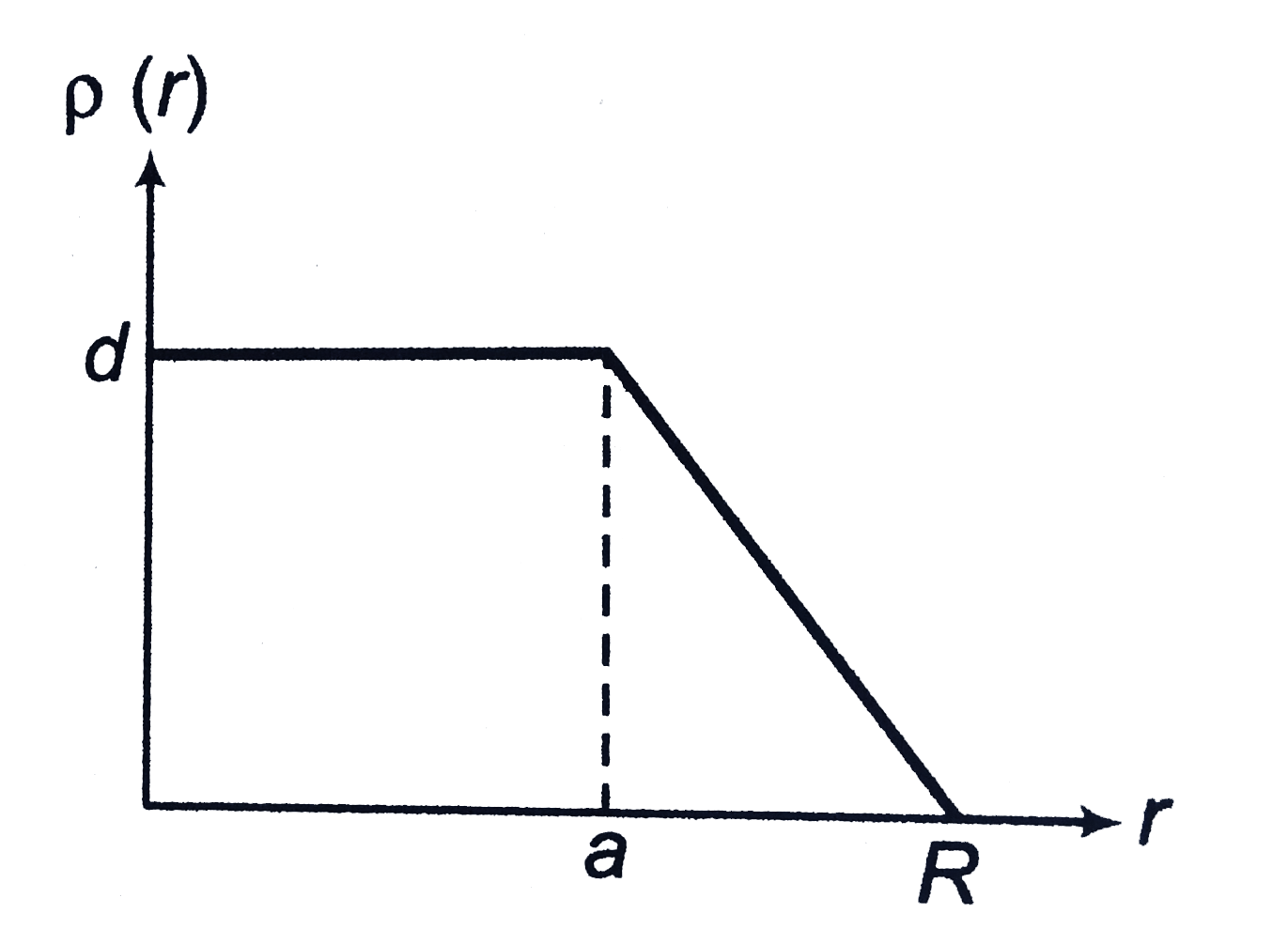
The electric field at r=R is
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA solid sphere of radius R has a charge Q distributed in its volume with a charge density rho=kr^a , where k and a are constants and r is the distance from its centre. If the electric field at r=(R)/(2) is 1/8 times that r=R , find the value of a.
View Solutionएक गोले जिसकी त्रिजिये R है आवेश का आयतन घनत्व ρ=kr है जहाँ r गोले के केंद्र से दुरी है तथा k नियतांक है गोले की षेरेस्ट पर विधुत क्षेत्र की त्रीवता का परिमाण है
View Solutionत्रिज्या R के एक ठोस गोले के सम्पूर्ण आयतन में आवेश Q को इस प्रकार बाँटा गया है कि आवेश-घनत्व p=kra है। यहाँ k तथा a व नियतांक हैं तथा r गोले के केन्द्र से दूरी है। यदि इस गोले में r=R2 पर विद्युत का मान r= R पर विद्युत क्षेत्र के मान का 18 है, तो नियतांक a का मान निकालें।
View SolutionAn insulating solid sphere of the radius R is charged in a non - uniform manner such that the volume charge density ρ=Ar, where A is a positive constant and r is the distance from the centre. The potential difference between the centre and surface of the sphere is
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View SolutionA solid sphere of radius R has a mass distributed in its volume of mass density rho=rho_(0) r, where rho_(0) is constant and r is distance from centre. Then moment of inertia about its diameter is
View Solution[" A solid sphere of radius "R" is charged with "],[" volume charge density "rho=Kr^(n)," where "K" and "n],[" are constants and "r" is the distance from its "],[" centre.If electric field inside the sphere at "],[" distance "r" is proportional to "r^(4)," then find the "],[" value of "n.]
View SolutionA solid sphere of radius R is charged with volume charge density p=Krn , where K and n are constants and r is the distance from its centre. If electric field inside the sphere at distance r is proportional to r4 ,then find the value of n.
View Solutionएक कुचालक गोले की त्रिज्या R तथा उसका आयतन आवेश घनत्व ρ है। दूरी r(r<R) पर विधुत क्षेत्र का मान होगा :-
View SolutionCharge density of a sphere of radius R is rho = rho_0/r where r is distance from centre of sphere.Total charge of sphere will be
View Solution
