Four point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.Solution in Gujrati
The correct Answer is:(v0)min=3m/s,K=3×10−4J
In the figure
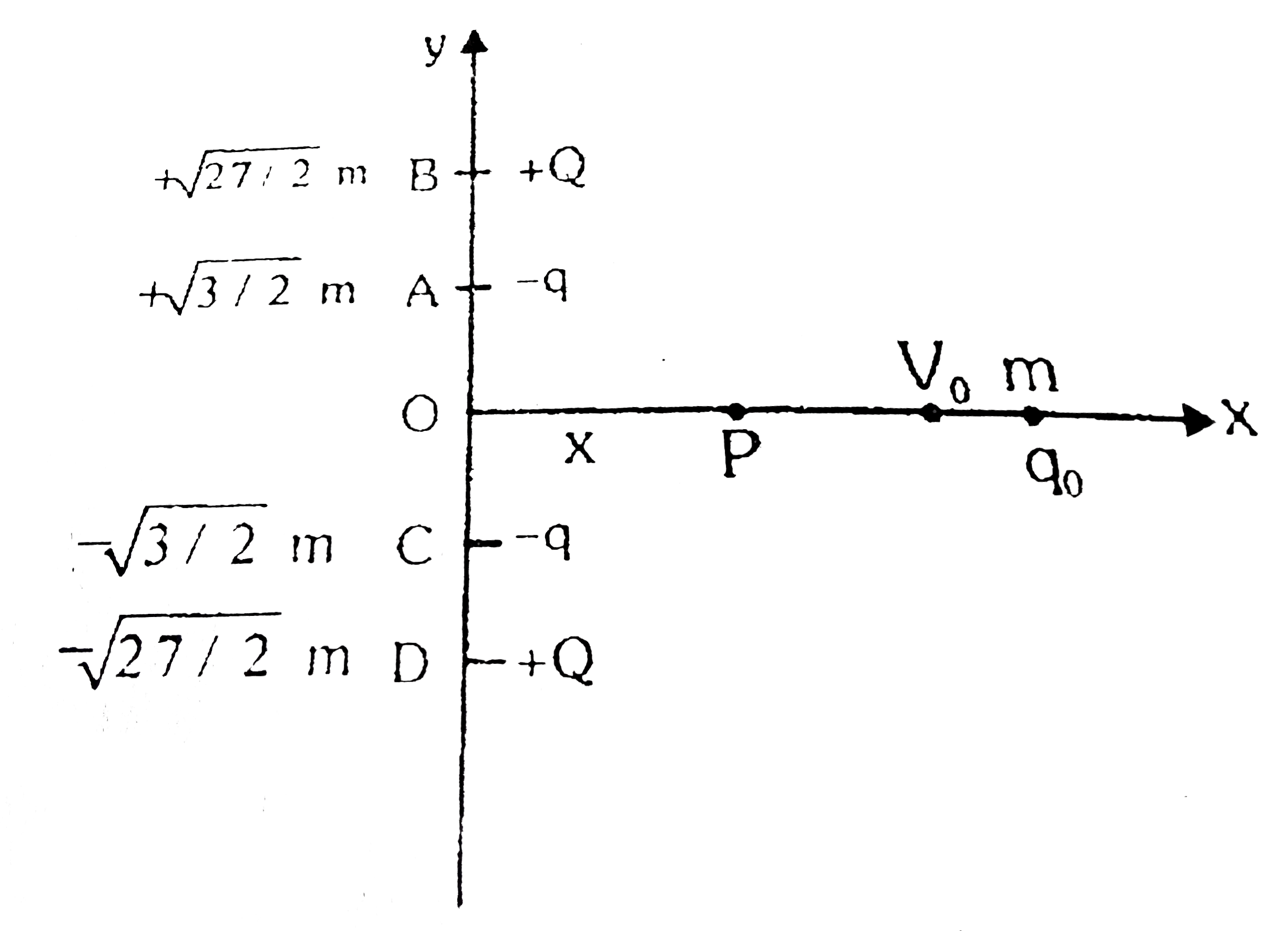
q=1μC=10−6C,q0=+0.1μC=10−7C
and
m=6×10−4kg and Q=8μC=810−6C
Let P be any point at a distance x from origin O. Then
AP=CP=√32+x2
BP=DP=√272+x2
Electric potential at point P will be
V=2KQBP−2KqAP
where K=14πε0=9×109N/m2/C2
∴V=2×9×109⎡⎢
⎢⎣8×10−6√272+x2−10−6√32+x2⎤⎥
⎥⎦
V=1.8×104⎡⎢
⎢⎣8√272+x2−1√32+x2⎤⎥
⎥⎦ ...(i)
∴ Electric field at P is
E=−dVdx=1.8×104
⎡⎣(8)(−12)(272+x2)−32−(−12)(32+x2)−32⎤⎦(2x)
E=0 on x-axis where −x=0 or
8(272+x2)3/2=1(32+x2)3/2
⇒(4)3/2(272+x2)3/2=1(32+x2)3/2
⇒(272+x2)=4(32+x2)
This equation gives x=±√52m
The least value of kinetic energy of the particle at infinity should be enough to take particle upto
x=+√52m because at x=+√52m,E=0
⇒ Electrotatic force on charge q is zero or Fe=0. For at x>√52m, E is repulsive (towards x-axis) and for x<√52m, E is attractive (towards negative x-axis).
Now, from Eq. (i) potential at x=√52m
v=1.8×104⎡⎢
⎢⎣8√272+52−1√32+52⎤⎥
⎥⎦
⇒V=2.7×104 volt
Applying energy conservation at x=∞ and x=√52m,12mv20=q0V ...(ii)
∴v0=√2q0Vm
Substituting the values
v0=√2×10−7×2.7×1046×10−4⇒v0=3m/s
∴ Minimum value of v0 is 3m/s
From eq. (i) potential at origin (x=0) is
V0=1.8×104⎡⎢
⎢⎣8√272−1√32⎤⎥
⎥⎦≈2.4×104V
Let K be the kinetic energy of the particle at origin. Applying energy conservation at x=0 and x=∞
K+q0V0=12mv20 But 12mv20=q0V [from Eq. (ii)]
K=q0(V−V0)=(10−7)(2.7×104−2.4×104)
⇒K=3×10−4J
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - PHY
68 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-1
121 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - LINKED COMPREHENSION TYPE
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Find roots equation 2x2−x−3=0.
View SolutionIf the vectors →a,→b,and→c form the sidesBC,CAandAB, respectively, of triangle ABC,then
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
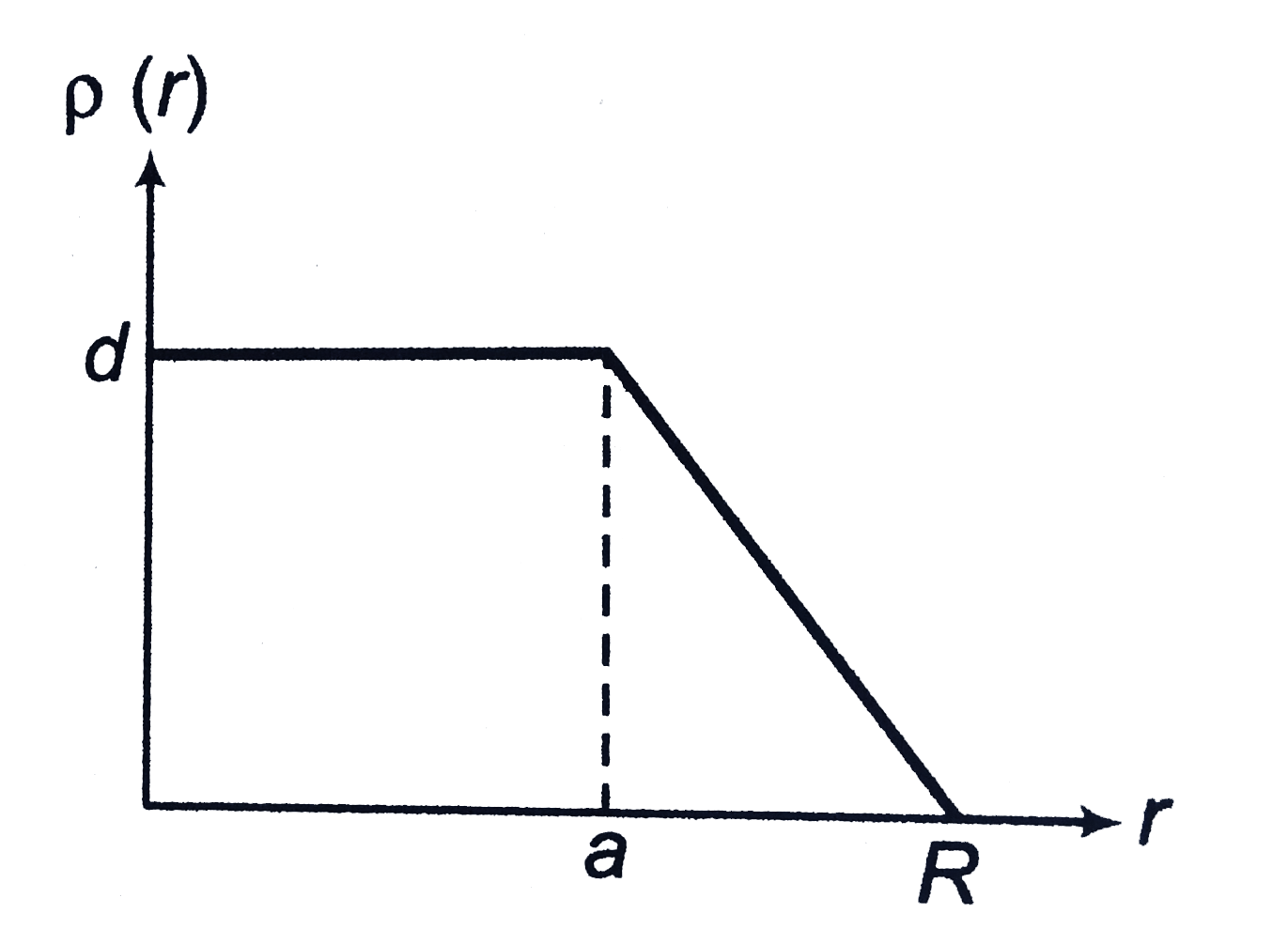
The electric field at r=R is
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionFour point charges +8mC , -mC , and +8mC are fixed at the points -sqrt(27/2)m , -sqrt(3/2)m , +sqrt(3/2)m and +sqrt(27/2)m respectively on the y-axis. A particle of mass 6xx10^-4kg and charge +0.1muC moves along the -x direction. Its speed at x=+oo is V_0 . Find the least value of V_0 for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. Given (1)/(4piepsilon_0)=9xx10^9Nm^2//C^2 .
View SolutionFour point + 8 mu C, -1 mu C, -1 mu C , and + 8 mu C are fixed at the points -sqrt(27//2) m, - sqrt(3//2) m, +sqrt(3//2) m , and +sqrt(27//2) m , respectively, on the y - axis. A particle of mass 6 xx 10^-4 kg and charge + 0.1 mu C moves along the x- direction. Its speed at x = + oo is V_0 . Find the least value of V_0 for which the particle will cross the origin. Find also the kinetic energy of the particle at the origin. Find also the kinetic energy of the particle at the origin. Assume that space is gravity free. Given (1// 4 pi epsilon_0) = 9 xx 10^9 Nm^2 C^-2 .
View SolutionA charged particle (charge q, mass m) has velocity v_(0) at origin in +x direction. In space there is a uniform magnetic field B in -z direction. Find the y coordinate of particle when is crosses y axis.
View SolutionTwo point charges each 50μC are fixed on y-axis at y=+4m and y=−4m. Another charged particle having charge −50μC and mass 20g is moving along the positive x-axis. When it is at x=−3m , its speed is 20m/sec. Find the speed of charged particle when it reaches to origin. Also , find distance of charged particle from origin , when its kinetic energy becomes zero.
View SolutionA particle whose velocity is given as vecv=hati+6thatjm//s is moving in x-y plane. At t-0, particle is at origin. Find the radius of curvature of path at point ((sqrt(2))/(3)m,(2)/(3)m)
View SolutionA particle is moving along positive X direction and is retarding uniformly. The particle crosses the origin at time t=0 and crosses the point x=4.0m at t=2s.
(a) Find the maximum speed that the particle can possess at x=0.
(b) Find the maximum value of retardation that the particle can have.
View SolutionFour point charges +8μC,−1μC,−1μC and , +8μC are fixed at the points −√27/2m,−√3/2m,+√3/2m
and +√27/2m respectively on the y-axis. A particle of mass 6×10−4kg and +0.1μC moves along the x-direction. Its speed at x=+∞ is v0. find the least value of v0 for which the particle will cross the origin. find also the kinetic energy of the particle at the origin in tyhis case. Assume that there is no force part from electrostatic force.
View SolutionA particle of mass m=5kg is moving with a uniform speed v=3√2 in the XOY plane along the line Y=X+4. The magnitude of the angular momentum of the particle about the origin is
View SolutionA point particle of mass m is released from a distance sqrt(3)R along the axis of a fixed ring of mass M and radius R as shown in figure. Find the speed of particle as it passes through the centre of the ring.
View SolutionFour point charges q, -2q, -q and 2q are placed at points (0,0,0) m , (√2,0,0)m,(√2,√2,0)m and (0,√2,0) m respectively . The electric field at point (1√2,1√2,0)m is (q=1μC)
View Solutionचार बिन्दु आवेश +8μC,−1μC,−1μC तथा +8μC, y- अक्ष पर क्रमशः बिन्दुओं −√27/2 मी, −√3/2 मी, +√3/2 मी तथा +√27/2 मी पर स्थित हैं। 6×10−4 किग्रा द्रव्यमान तथा +0.1 μC आवेश का एक कण x- दिशा के अनुदिश चलता है। इसकी x=+∞ पर चाल v0 हैं।v0 का वह न्यूनतम मान ज्ञात कीजिए जिसके लिए कण मूल बिन्दु से गुजर जायेगा , मूल विन्दु पर कण की गतिज ऊर्जा भी ज्ञात कीजिए। मान लीजिए कि स्थान गुरुत्वहीन है। (दिया है- 4pi epsi_(0)=9 xx 10^(9) "न्यूटन-मी"^(2)" कूलॉम"^(-2))
View Solution
