A non-conducting disc of radius a and uniform positive surface charge density σ is placed on the ground, with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc, from a height H with zero initial velocity. The particle has q/m=4∈0g/σ
(a) Find the value of H if the particle just reaches the disc.
(b) Sketch the potential energy of the particle as a function of its height and find its equilibrium position.Solution in Gujrati
The correct Answer is:(i) H=43a (ii) H=a√3
Potential at a height H on the axis of the disc V(P):
The charge dq contained in the ring shown in figure.
Potential of p due to this ring

dV=14πε0.dqx where x=√H2+r2
dV=14πε0.(2πrdr)σ√H2+r2=(σ2ε0)×(rdr√H2+r2)
∴ Potential due to the complete disc
Vp=r=a∫r=0dV=σ2ε0r=a∫r=0rdr√H2+r2
Vp=σ2ε0[√a2+H2−H]
Potential at centre (O) will be VO=σa2ε0∴H=0
(i) Particle is released from P and just reaches point O. Therefore from conservation of mechanical energy.
Decrease in graviational potential energy
= Increase in electrostatic potential energy
(ΔKE=0 because K1=Kf=0)
∴mgh=q[Vo−Vp]⇒gH=(qm)(σ2ε0)
[a−√a2+H2+H] ...(i)
qm=4ε0gσ∴qσ2ε0m=2g
Substituting in Eq. (i), we get
gH=2g[a+H−√a2+H2]
⇒H2=(a+H)−√a2+H2
⇒√a2+H2=a+H2
⇒a2+H2=a2+H24+aH⇒34H2=aH
⇒H=43a and H=0∴H=(43)a
(ii) Potential energy of the particle at height H=Electrostatic potential energy + gravitational potential energy
∴U=qV+mgH
Here V=Potential at height H
U=σq2ε0[√a2+H2−H]+mgH ...(ii)
At equilibrium position F=−dUdH=0
Differentialting Eq. (ii) w.r.t H
⇒mg+σq2ε0[(12)(2H)1√a2+H2−1]=0
(∵σq2ε0=2mg)
∴mg+2mg[H√a2+H2−1]=0
⇒1+2H√a2+H2−2=0⇒2H√a2+H2=1
⇒H2a2+H2=14⇒3H2=a∘⇒H=a√3
From Eq. (ii) we can write U-H equation as
U=mg(2√a2+H2−H)
(Parabolic variation)
U=2mga at H=0
and U=Umin=√3mga at H=a√3
therefore, U−H graph will be as shown.
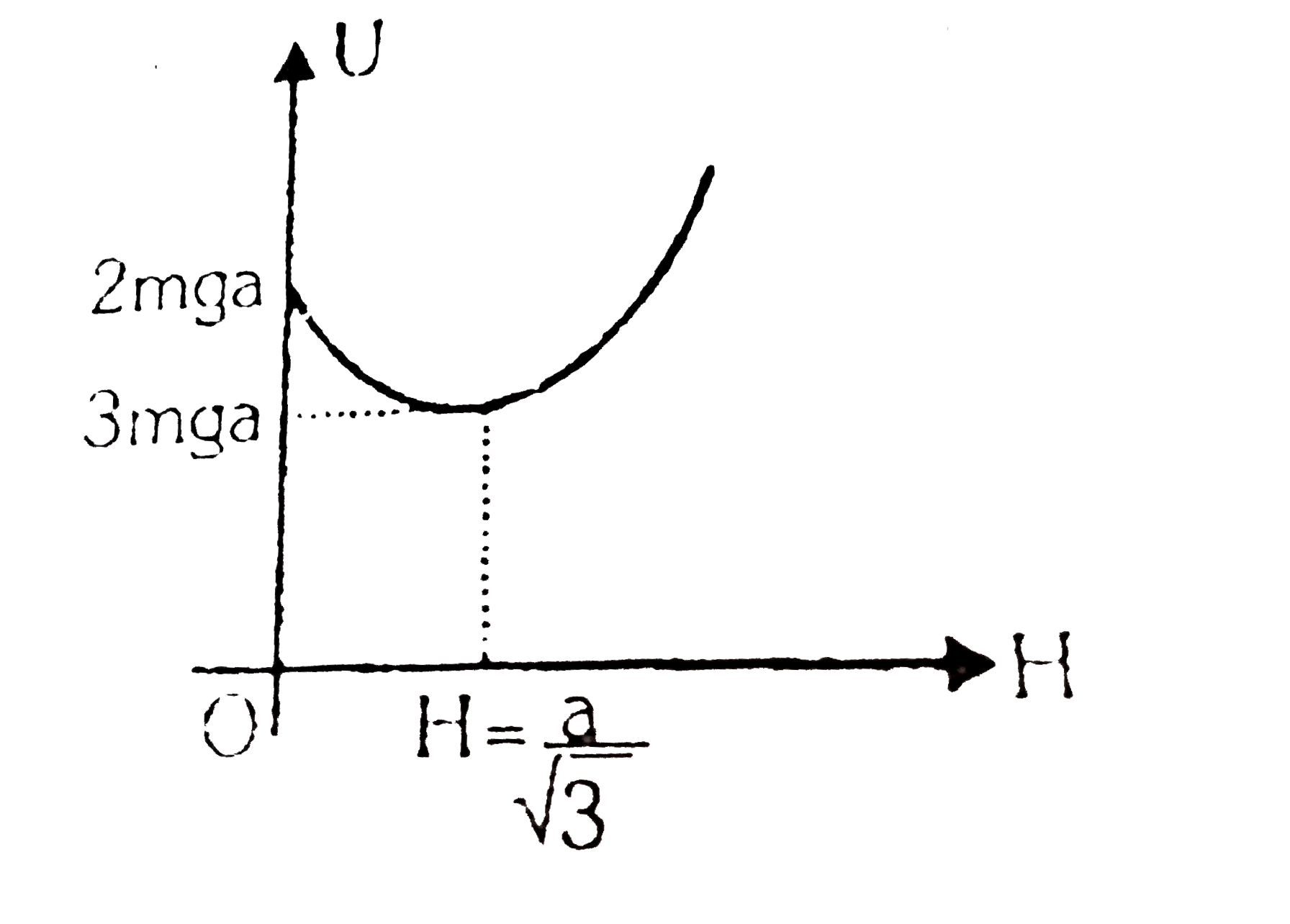
Note that at H=a√3, U is minimum.
Therefore, H=a√3 is stable equilibrium position.
Topper's Solved these Questions
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - PHY
68 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - EXERCISE-1
121 Videos
- MISCELLANEOUSBOOK - ALLEN CHAPTER - MISCELLANEOUSEXERCISE - LINKED COMPREHENSION TYPE
3 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
- PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV
7 Videos
Similar Questions
Find roots equation 2x2−x−3=0.
View SolutionIf the vectors →a,→b,and→c form the sidesBC,CAandAB, respectively, of triangle ABC,then
View SolutionThe nuclear charge (Ze) is non uniformlly distribute with in a nucleus of radius r. The charge density ρ(r) (charge per unit volume) is dependent only on the radial distance r form the centre of the nucleus s shown in figure. The electric field is only along the radial direction.
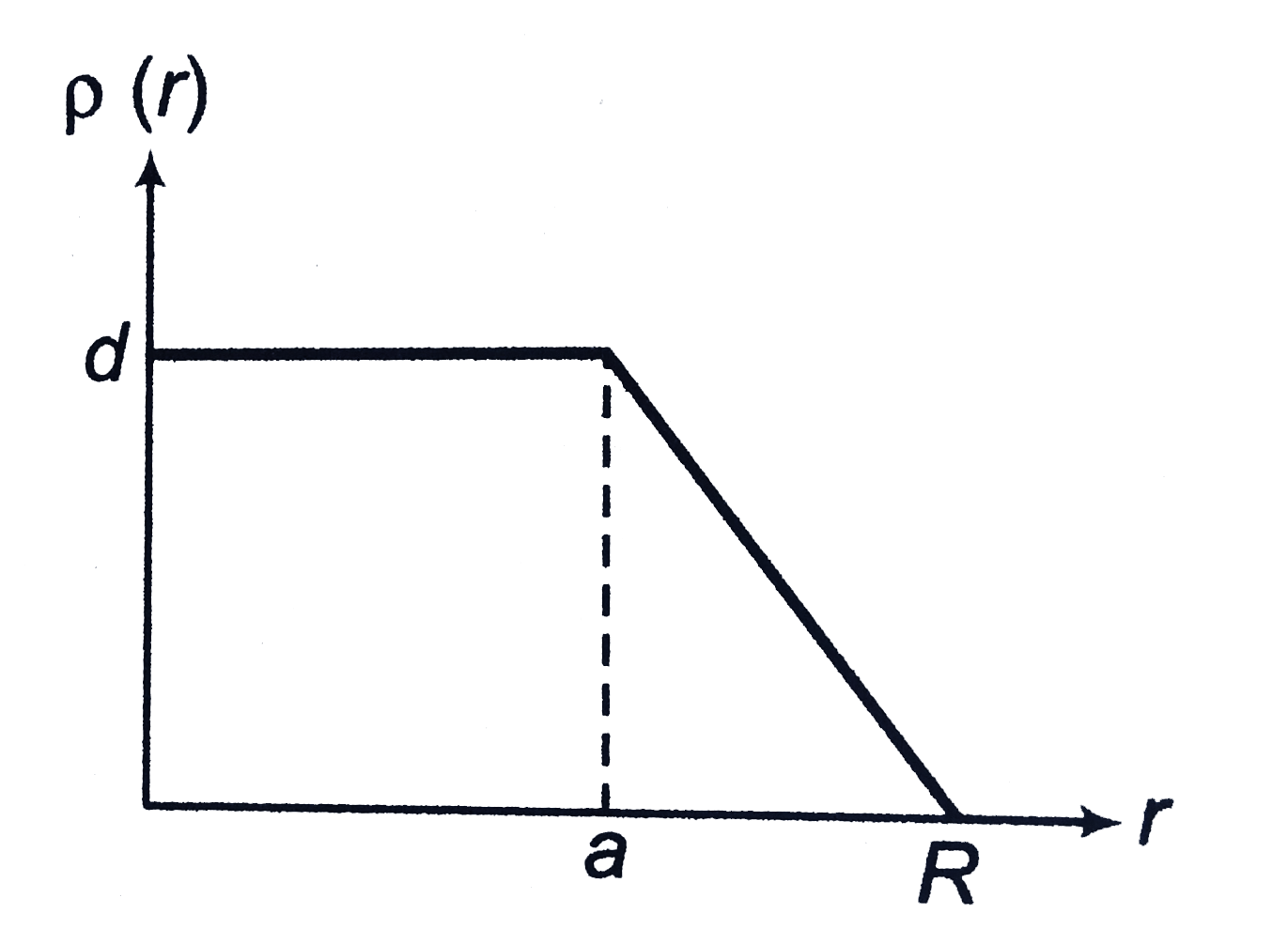
The electric field at r=R is
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.
View SolutionA positively charged disc is placed on a horizontal plane. A charged particle is released from a certain height on its axis. The particle just reaches the centre of the disc. Select the correct alternative.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density sigma . The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity omega . Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionA charge q is placed at the some distance along the axis of a uniformly charged disc of surface charge density σ. The flux due to the charge q through the disc is ϕ. The electric force on charge q exerted by the disc is
View SolutionA non-conducting thin disc of radius R and mass m having charge uniformly over one side with surface density sigma rotates about its axis with an angular velocity omega . Find : (a) the magnetic induction at the centre of the disc, (b) the magnetic moment of the disc. ( c) the ratio of magnetic moment and angular momentum of disc.
View SolutionA dielectric disc of radius R and uniform positive surface charge density σ is placed on the grup with its axis vertical. A particle of mass m and positive charge q is dropped, along the axis of the disc from a height H with dropped, along the axis of the disc from a height H with zero intial velocity. The charge -mass ratio of the particle is qm=4εon0gσ.
(i). Find the value of H if the particle just reaches the disc.
(ii). Sketch the potential energy of the particle as a function of its height and find its height in equilibrium position.
View SolutionThere is uniformly charged disc of surface charge density sigma and of radius 1m . H=10m height below the disc is a gun which is continuously emitting a charged particle and its isotopic in the vertically upward direction. The particles are charged through same potential before being emitted. The charge of the particle is q=8xx10^(-19)C . The difference of potential energies of particle and the isotopic at B is 10^(-23) Joule. Also the velocity of the particle at B is zero. The ratio of masses of particle and isotopic is (3)/(2) . If the total energy of isotope at B is 1.1kxx10^(-23)J Then find k ..(Given sigma//epsilon_(0)=10^(-4)N//C ).
View SolutionA non-conducting disc having unifrom positive charge Q , is rotating about its axis with unifrom angular velocity omega .The magnetic field at the centre of the disc is.
View SolutionA non-conducting disc of radius a with uniform positive surface charge density σ is placed on the ground with its axis vertical. A particle of mass m and positive charge q is dropped along the axis of the disc from a height H with zero initial velocity. Charge per unit mass of the particle is qm=4ε0gσ.
(i) Find the value of H if the particle just reaches the disc.
View SolutionA non-conducting disc of radius a with uniform positive surface charge density sigma is placed on the ground with its axis vertical. A particle of mass m and positive charge q is dropped along the axis of the disc from a height H with zero initial velocity. Charge per unit mass of the particle is q/m = (4 epsilon_0 g)/(sigma) . (ii) Find the height for its equilibrium position.
View SolutionA non - conducting disc of radius R is uniformly charged with surface charge density σ. A disc of radius R2 is cut from the disc, as shown in the figure. The electric potential at centre C of large disc will be

View Solutionएक कुचालक चकती जिसकी त्रिज्या a एवं समरूप क्षेत्रिय आवेश घनत्व σ है, को जमीन पर रखा गया है इसके केन्द्र से गुजरने वाला अक्ष उर्ध्वाधर है| m द्रव्यमान एवं q आवेश का कण अक्ष के अनुदिश H ऊँचाई से शून्य प्रारम्भिक वेग से छोडा गया। कण के लिये qm=4ε0gσ
(a) यदि कण चकती तक पहुँच जाए इसके लिये H का मान ज्ञात करें।
(b) कण की स्थितिज ऊर्जा का ऊँचाई के साथ ग्राफ बनाये एवं साम्यावस्था की स्थिति ज्ञात करें।
View Solution
