As a particle moves along the x−axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
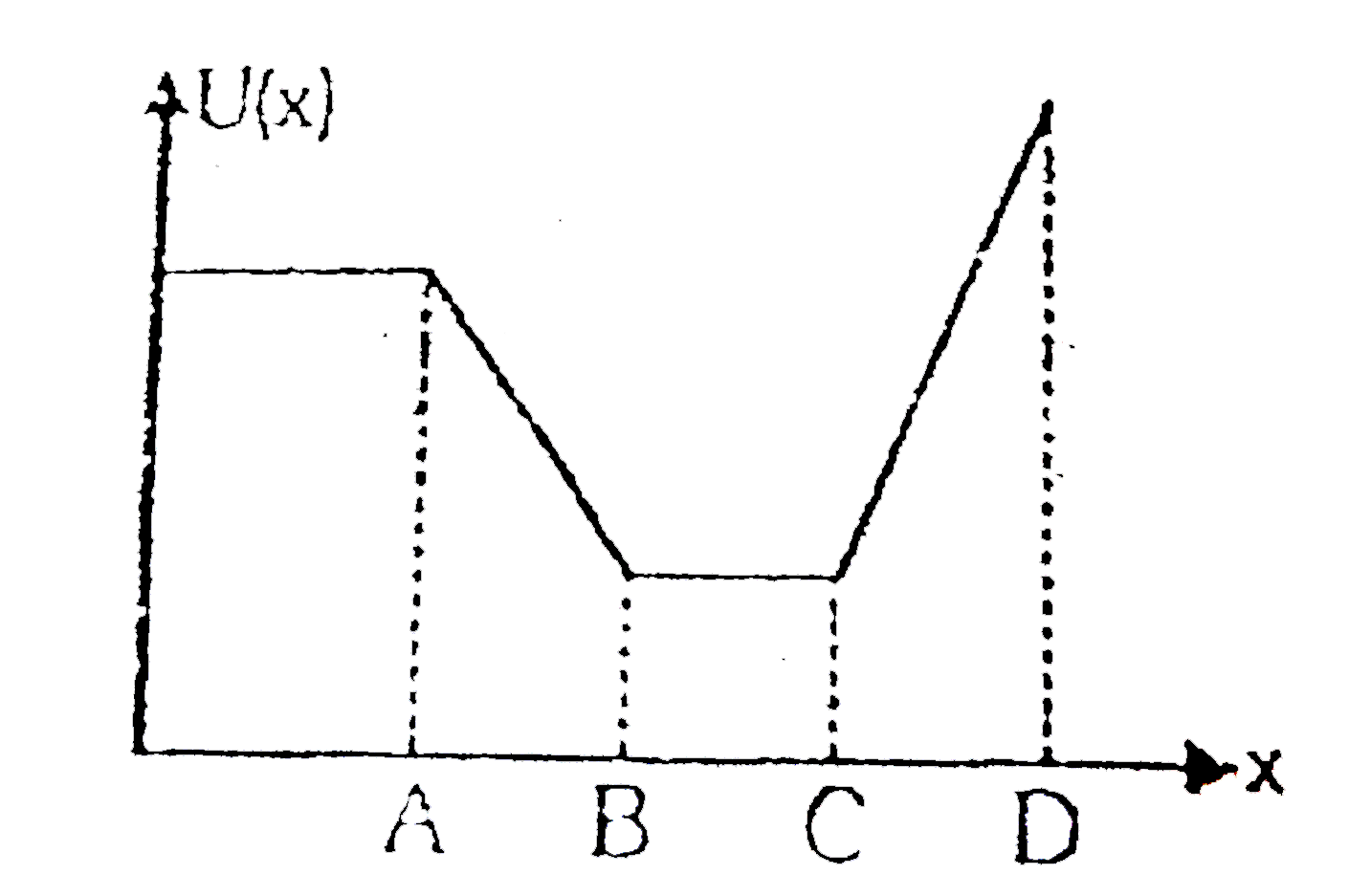 Solution in Gujrati
Solution in Gujrati
AB, BC, CD
AB, CD, BC
BC, CD, AB
BC, AB, CD
The correct Answer is:D
−dUdx−F
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View SolutionIn figure, the variation of potential energy of a particle of mass m=2kg is represented w.r.t its x-coordinate. The particle moves under the effect of the conservative force along the x-axis. Which of the following statements is incorrect about the particle?
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis. Which of the following statements are correct about the particle:
View SolutionIn the figure the variation of potential energy of a particle of mass m=2kg is represented w.r.t. its x-coordinate. The particle moves under the effect of this conservative force along the x-axis.
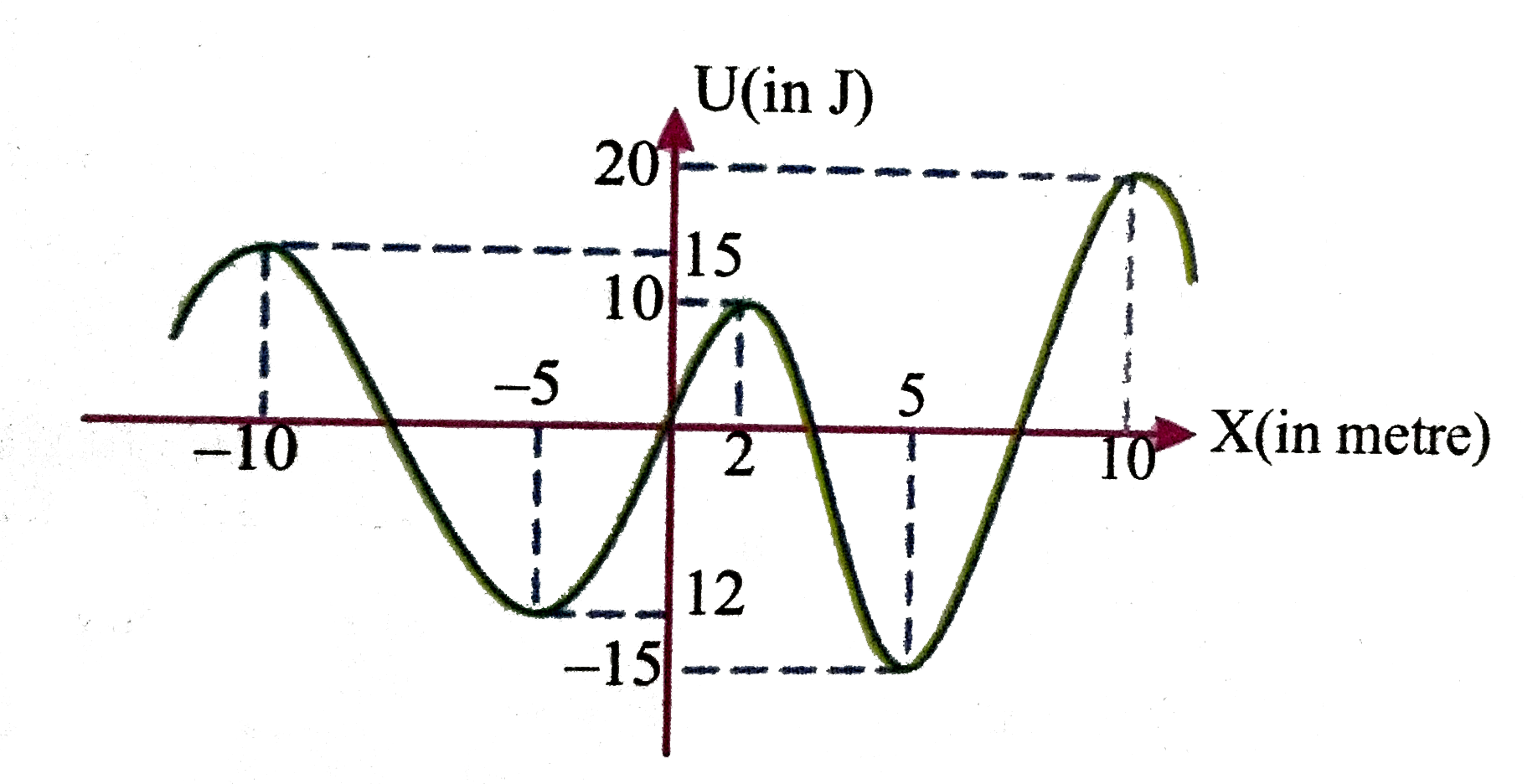
If the particle is released at the origin then
View SolutionIn the figure, the variation of potential energy of a particle of mass m = 2kg is represented with respect to its x-coordinate. The particle moves under the effect of this conservative force along the X-axis.
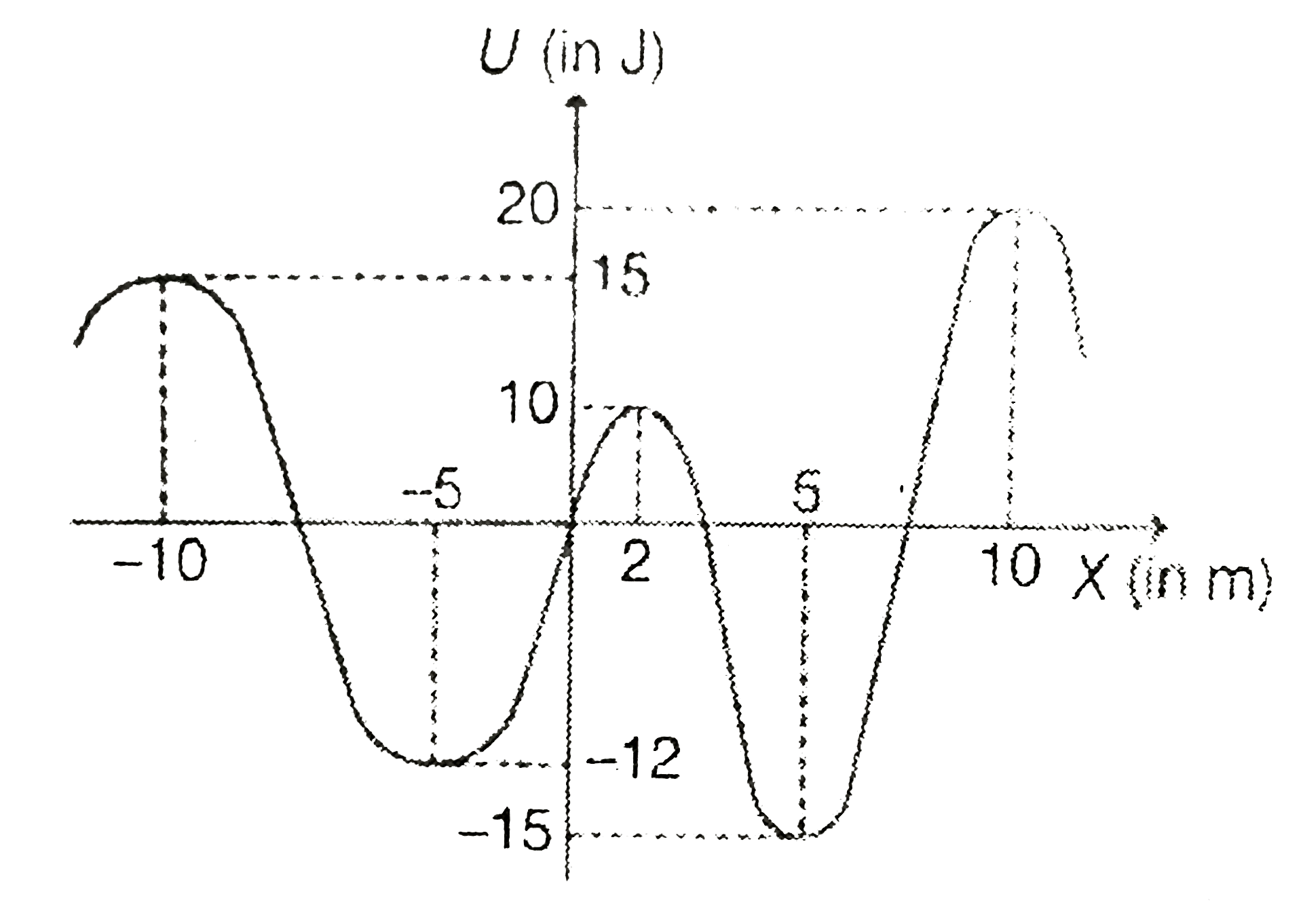
If the particle is released at the origin, then
View SolutionThe kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is -
View SolutionA conservative force acts on a particle as the particle moves along the positive x-axis from origin origin to x=2m . The force is parallel to x-axis. Now, consider four different cases, as shown in the figures, 1, 2, 3, and 4, where the forces is shown as a function of x. Rank the situations according to the change in potential energy associated with the force, least ( or most negative) to greatest ( or most positive).
View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View SolutionThe variation of potential energy of a particle of mass m = 5kg to its x-coordinate . The particle moves under the effect of this conservative force only along the x-axis. Then, choose the correct option.
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure The magnitude of force acting on particle at x = 9 mis
View SolutionA conservative force F(x) act on a 1kg particle. The potential energy U(x)=(x-4)^(2) , At x=5 ,particle has kinetic energy of 24J .The greatest value of x to which particle can move is
View SolutionFigure shows the displacement of a particle going along the X-axis as a function of time. The force acting on the particle is zero in the region

View Solution
