A particle of mass m is moving with constant speed in a vertical circle in X−Z plane. There is a small both at some distance on Z−axis. The maximum distance of the shadow of the particle on X−axis from origin equal to :−
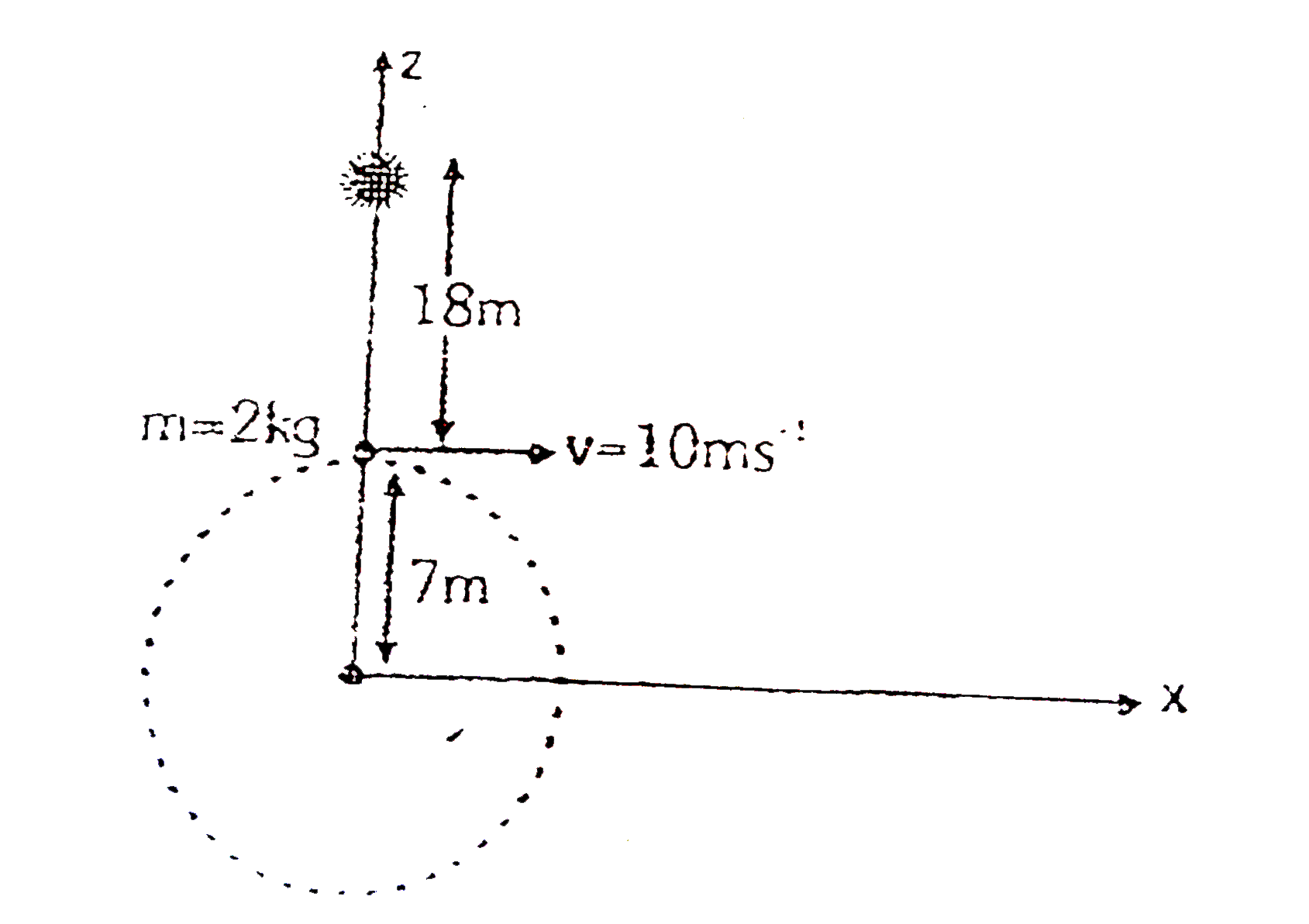 Solution in Gujrati
Solution in Gujrati
17524m
12524m
25m
24m
The correct Answer is:A
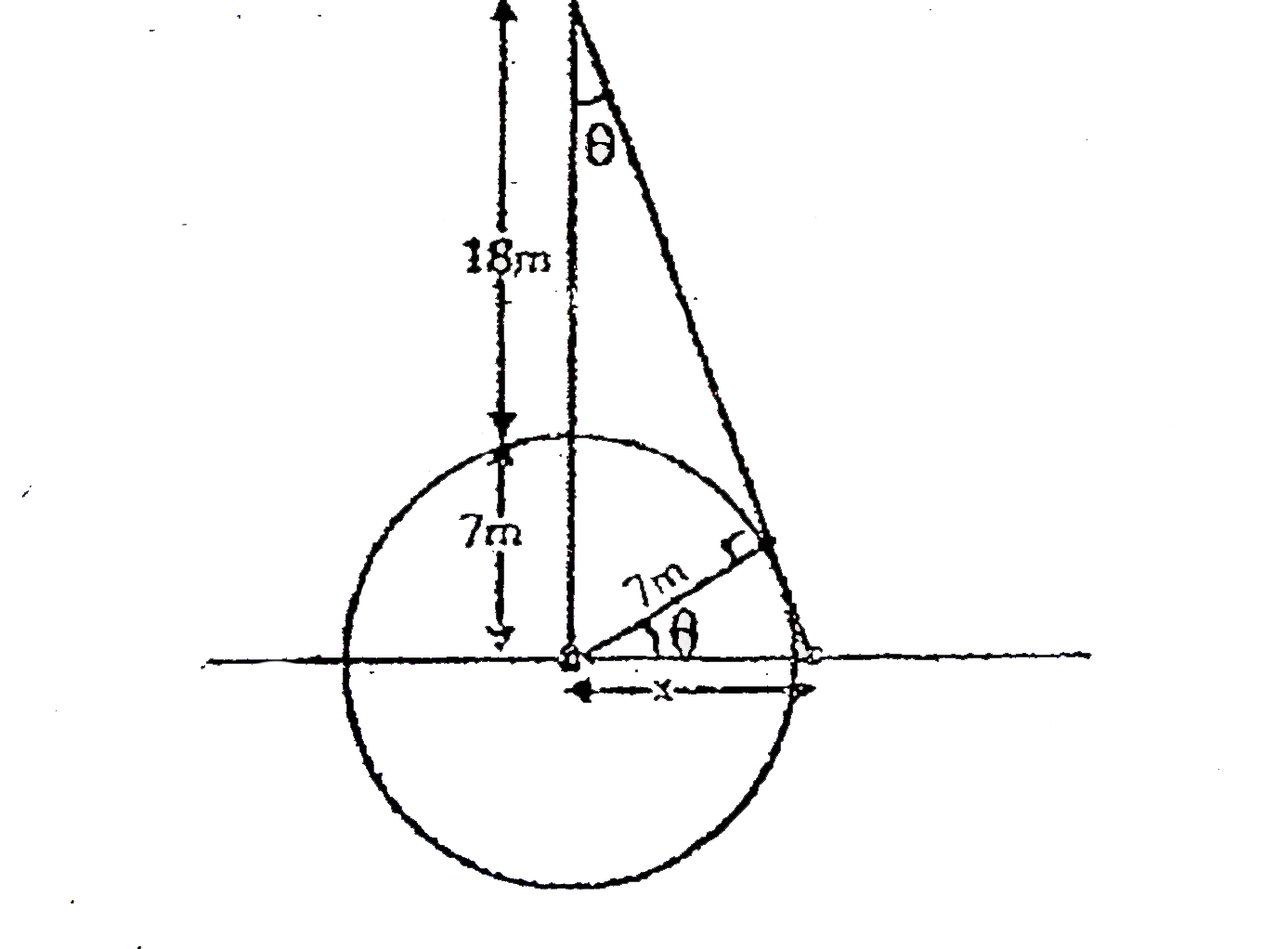
sinθ=725,cosθ=2425
xcosθ=7⇒x=7cosθ=7×2524=17524m
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View SolutionA particle of mass m is released in vertical plane from a point P at x=x0 on the x-axis. It falls vertically parallel to the y-axis. Find the torque τ acting on the particle at a time about origin.

View SolutionA particle is projected from the horizontal x-z plane, in vertical x-y plane where x-axis is horizontal and positive y-axis vertically upwards. The graph of y coordinate of the particle v/s time is as shown . The range of the particle is sqrt3 . Then the speed of the projected particle is:
View SolutionA particle of mass 0.75 kg is moving in the XY plane parallel to Y-axis, with a uniform speed of 4 m/s. It crosses the X-axis at 3 m from the origin. What is the angular momentum of the particle about the origin?
View Solutionद्रव्यमान m अचर वेग से X-अक्ष के समान्तर एक रेखा में गति कर रहा है। मूलबिन्दु अथवा Z-अक्ष के सापेक्ष इसका कोणीय संवेग ।
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View SolutionFind the distance of the z-axis from the image of the point M(2−3,3) in the plane x−2y−z+1=0.
View SolutionA Particle of mass M is moving in a straight line with uniform speed v parallel to x - axis in X - Y plane at a height .h. from the X - axis. Its angular momentum about the origin is
View Solution(A) : The angular momentum of a particle w.r.t origin moving parallel to x-axis with constant velocity is constant. (R ) : There is no change in the perpendicular distance of the particle from the origin when it travels prallel to x-axis.
View SolutionA Particle of mass M is moving in a straight line with uniform speed v parallel to x-axis in X-Y plane at a height .h. from the X-axis. Its angular momentum about the origin is
View Solution(A): The angular momentum of a particle w.r.t origin moving parallel to x -axis with constant velocity is constant
(R): There is no change in the perpendicular distance of the particle from the origin when it travels prallel to x-axis.
View Solution(A) : The angular momentum of a particle w.r.t origin moving parallel to x-axis with constant velocity is constant.
(R ) : There is no change in the perpendicular distance of the particle from the origin when it travels prallel to x-axis.
View Solution
