A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre V02r. The translational velocity when the sphere starts pure rolling motion is Solution in Gujrati
V05
V07
V03
6V07
The correct Answer is:D
Step by step video & image solution for A sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V_(0) and rotational velocity about the centre (V_(0))/(2r). The translational velocity when the sphere starts pure rolling motion is by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
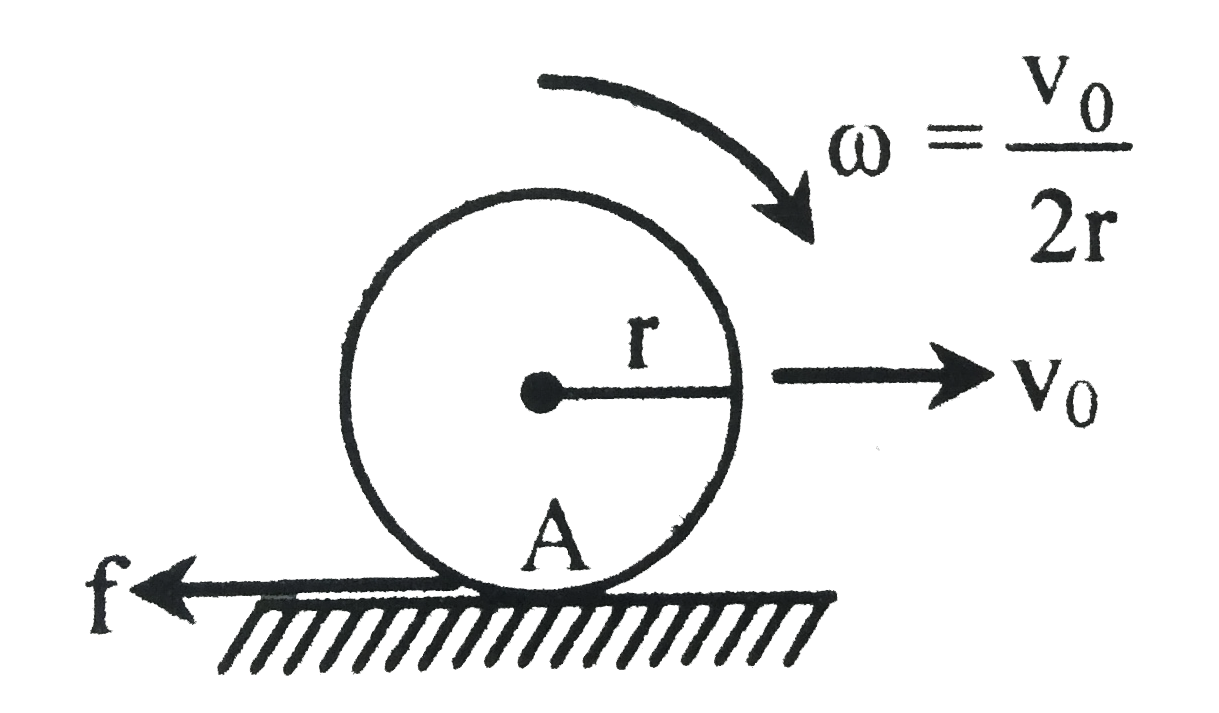 .
.
View SolutionA uniform ring of radius R is given a back spin of angular velocity V_(0)//2R and thrown on a horizontal rough surface with velocity of centre to be V_(0) . The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity omega_(0) . Once the pure rolling starts let v_(1) and v_(2) be the linear speeds of their centres of mass. Then
View SolutionA sphere of mass M and radius r shown in the figure on a rough horizontal plane. At some instant it has translational velocity v_(0) , and rotational velocity about centre v_(0)//2r . The percentage change of translational velocity after the sphere start pure rolling:
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View SolutionA sphere of mass M and radius r slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre V02r. The translational velocity when the sphere starts pure rolling motion is
View SolutionA solid sphere and a hollow sphere of equal mass and radius are placed over a rough horizontal surface after rotating it about its mass centre with same angular velocity ω0. Once the pure rolling starts let v1 and v2 be the linear speeds of their centres of mass. Then
View SolutionA sphere of mass m and radius R is kept on a rough floor. A sharp impulse is applied in the horizontal direction at the height of centre of sphere so that sphere acquires a linear velocity v0 without any angular velocity. Calculate the velocity of sphere when pure rolling starts.
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At some instant it has translational velocity V0 and rotational velocity about the centre v02r. Find the translational velocity after the sphere starts pure rolling.
 .
.
View SolutionA sphere of mass M and radius r shown in figure slips on a rough horizontal plane. At same instant it has translational velocity v0 and rotational velocity about the centre v0/2r. Find the translational velocity (in m/s) after the sphere start pure rolling (Take v0=7 m/s)
View SolutionA uniform ring of radius R is given a back spin of angular velocity V_(0)//2R and thrown on a horizontal sorgh surface with velocity of centre V_(0) . The velocity of the centre of the ring when it starts pure rolling will be
View SolutionA solid sphere has combined linear and rotation motion as shown in figure. The velocity of its centre of mass when it starts pure rolling is (R = radius of sphere)
View Solution
