Two particles P and Q are moving with velocity of (ˆi+ˆj) and (−ˆi+2ˆj) respectively. At time t=0, P is at origin and Q is at a point with positive vector (2ˆi+ˆj). Then the shortest distance between P & Q is :-Solution in Gujrati
2√55
4√55
√5
3√55
The correct Answer is:B
→vQP=−ˆi+2ˆj−ˆi−ˆj=−2ˆi+ˆj
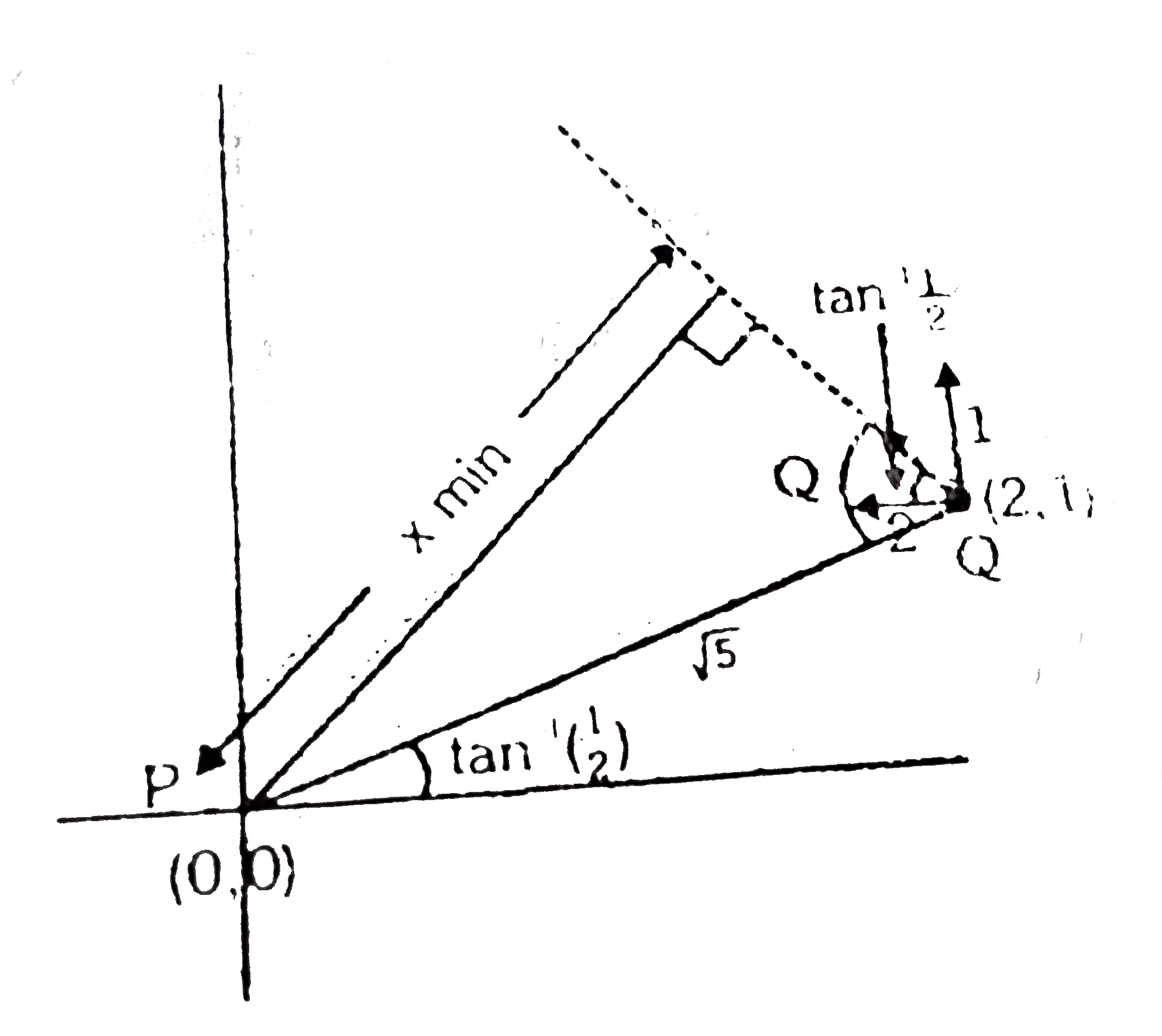
So from sine rule √5sin90∘=xminsinθ⇒xm
=√5×2sinθ2cosθ2
=√5×2×1√5×2√5=4√5
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionThe position vectors of the points P, Q, R are ˆi+2ˆj+3ˆk, −2ˆi+3ˆj+5ˆk and 7ˆi−ˆk respectively. Prove that P, Q and R are collinear points.
View SolutionLet p, q, r and s be respectively the magnitudes of the vectors 3ˆi−2ˆj,2ˆi+2ˆj+ˆk,4ˆi−ˆj+ˆk,2ˆi+2ˆj+3ˆk. Which one of the following is correct?
View SolutionIf vec(P)=hat(i)+2hat(j)+hat(k)andvec(Q)=3hat(i)+hat(j)-hat(k) then vec(P)xxvec(Q) is
View SolutionIf →P=ˆi+2ˆj−4ˆkand→Q=ˆi+2ˆj−ˆk then (→P+→Q)⋅(→P−→Q) is
View SolutionAn electric field →E=(2ˆi+ˆJ)NC exists in space. The potential difference (VP−VQ) between two points whose positions vectors
−→rP=ˆi+2ˆJ and −→rQ=2ˆi+ˆj+ˆk is
View SolutionTwo vectors P=2hat I +bhat j +2hat k and Q=hat i+hat j+hat k will be parallel if :
View Solutionबिन्दु P और Q के स्थिति सदिश क्रमशः ˆi+3ˆj−7ˆk तथा5ˆi−2ˆj+4ˆj है | ज्ञात कीजिए-
−−→PQ
View Solutionबिन्दु P और Q के स्थिति सदिश क्रमशः ˆi+3ˆj−7ˆk तथा5ˆi−2ˆj+4ˆj है | ज्ञात कीजिए-
∣∣∣−−→PQ∣∣∣
View Solutionबिन्दुओ P(ˆi+2ˆj−ˆk) और Q(−ˆi+ˆj+ˆk) को मिलाने वाली रेखा 2:1 को अनुपात में
बाह्य विभाजित करने वाले बिंदु का स्थिति सदिश ज्ञात कीजिए।
View Solutionदो बिन्दुओ के स्थिति सदिश क्रमश: P(2ˆi+ˆj+3ˆk) तथा Q(−4ˆi−2ˆj+ˆk) है। Q से गुजरने वाले तथा PQ के लंबवत समतल का समीकरण होगा -
View SolutionIf ¯¯¯P=ˆi+ˆj+ˆk,¯¯¯Q=2ˆi−ˆj−ˆk, then ¯¯¯P−¯¯¯Q is
View Solution
