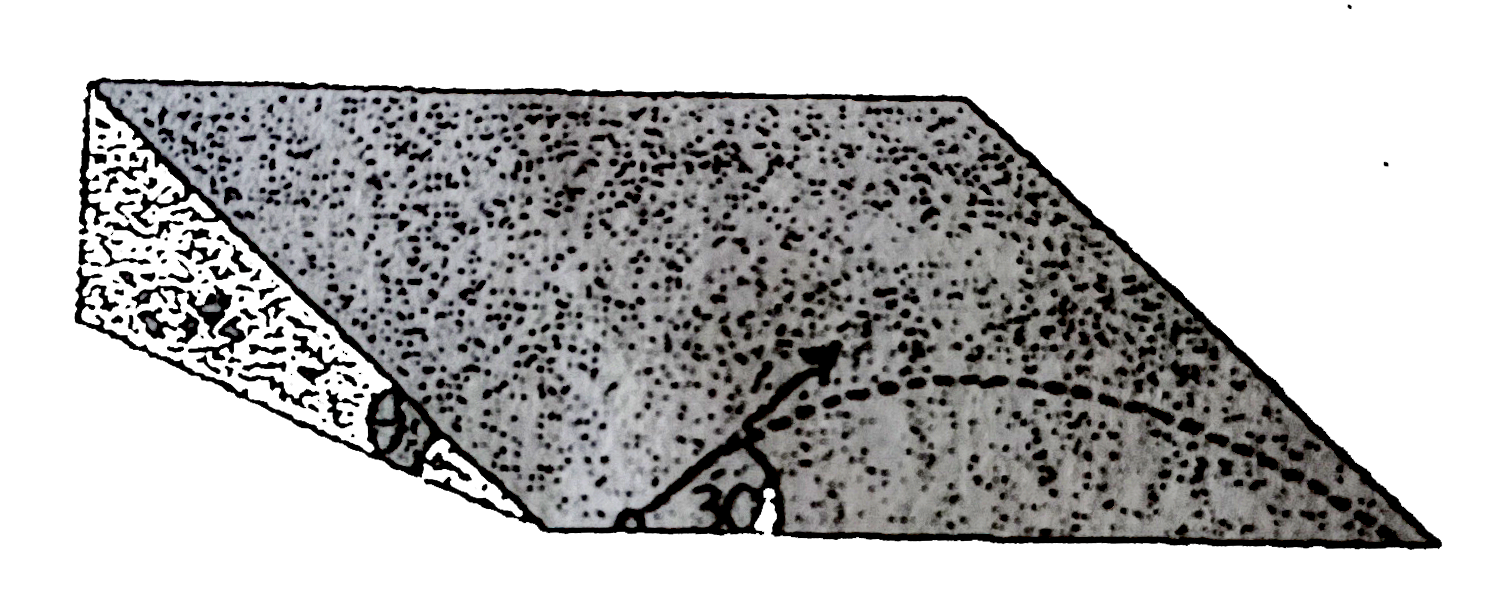
A small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.
 Solution in Gujrati
Solution in Gujrati
15∘
60∘
37∘
30∘
The correct Answer is:D

Along y-axis
Sy=uyt+12ayt2
here from O to P
Sy=0, t=2 sec, a=gsinθ
uy=10sin30=5m/s
0=5×2−12×10sinθ×4
1=2sinθ
sinθ=12
θ=30∘
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-02
57 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-2
89 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A particle is moving in a plane with velocity given by →u=u0ˆi+(aωcosωt)ˆj, where ˆi and ˆj are unit vectors along x and y axes respectively. If particle is at the origin at t=0. Calculate the trajectory of the particle :-
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionA student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA ball is projected on smooth inclined plane in direction perpendicular to line of greatest slope with velcoity of 8m/s. Find it's speed after 1sec.

View SolutionA ball is projected horizontally with a speed u from the top of inclined plane of inclination α with horizontal. At what distance along the plane, the ball will strike the plane ?
View SolutionA ball is projected perpendicularly from an inclined plane of angle theta , with speed 'u' as shown. The time after which the projectile is making angle 45^(@) with the inclined plane is :
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s along the direction at 30∘to the bottom edge of the slope .It returns to the edge after 2s . The ball is in contact with the inclied plane throughout the process. The angle of inclination θ is :−.

View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10 m//s along the direction at 30^(@) to the bottom edge of the slope. It returns to the edge after 2s. The ball is in constant with the inclined plane throughout the process. What is the inclination angle of the plane?
View SolutionA small ball is projected up a smooth inclined plane with an initial speed of 10m/s at 30∘ from the bottom edge of the slope. It returns to the edge after 2s. The ball is in contact with the inclined plane throughout the process. The inclination angle (in degree) of the plane is N. The value of N/6 is
View SolutionA ball is projected from the bottom of an inclined plane of inclination 30^@ , with a velocity of 30 ms^(-1) , at an angle of 30^@ with the inclined plane. If g = 10 ms^(-2) , then the range of the ball on given inclined plane is
View SolutionA ball is thrown upwards from the top of an incline with angle of projection theta with the vertical as shown. Take theta = 60^(@) and g=10 m//s^(2) . The ball lands exactly at the foot of the incline. The angle of inclination of incline alpha is:
View SolutionA projectile is projected upward with speed 2m//s on an incline plane of inclination 30^(@) at an angle of 15^(@) from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA projectile is projected upward with speed 2m/s on an incline plane of inclination 30∘ at an angle of 15∘ from the plane. Then the distance along the plane where projectile will fall is :
View SolutionA ball is projected perpendicularly from an inclined plane of angle theta , with speed 'u' as shown. The time after which the projectile is making angle 45^(@) with the inclined plane is :
View Solution
