The trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
![The trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2). [g=10 m//s^(2)] Maximum height H is :-](https://d10lpgp6xz60nq.cloudfront.net/physics_images/ALN_PHY_C02_E01_147_Q01.png)
Maximum height H is :-Solution in Gujrati
83
316
√3
2√3
The correct Answer is:B
Max. height H=u2sin2θ2g,10×(√32)22×10=38m
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#4
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#5
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#2
5 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A student performs an experiment to determine how the range of a ball depends on the velocity with which it is projected. The "range" is the distance between the points where the ball lends and from where it was projected, assuming it lands at the same height from which it was projected. It each trial, the student uses the same baseball, and launches it at the same angle. Table shows the experimental results.
∣∣ ∣ ∣ ∣ ∣ ∣∣TrailLaunch speed(m/s)Range(m)110822031.833070.7440122.5∣∣ ∣ ∣ ∣ ∣ ∣∣
Based on this data, the student then hypothesizes that the range, R, depends on the initial speed v0 according to the following equation : R=Cvn0, where C is a constant and n is another constant.
Based on this data, the best guess for the value of n is :-
View SolutionA circus wishes to develop a new clown act. Fig. (1) shows a diagram of the proposed setup. A clown will be shot out of a cannot with velocity v0 at a trajectory that makes an angle θ=45∘ with the ground. At this angile, the clown will travell a maximum horizontal distance. The cannot will accelerate the clown by applying a constant force of 10,000N over a very short time of 0.24s. The height above the ground at which the clown begins his trajectory is 10m.

A large hoop is to be suspended from the celling by a massless cable at just the right place so that the clown will be able to dive through it when he reaches a maximum height above the ground. After passing through the hoop he will then continue on his trajectory until arriving at the safety net. Fig (2) shows a graph of the vertical component of the clown's velocity as a function of time between the cannon and the hoop. Since the velocity depends on the mass of the particular clown performing the act, the graph shows data for serveral different masses.

If the angle the cannot makes with the horiaontal is increased from 45∘, the hoop will have to be
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
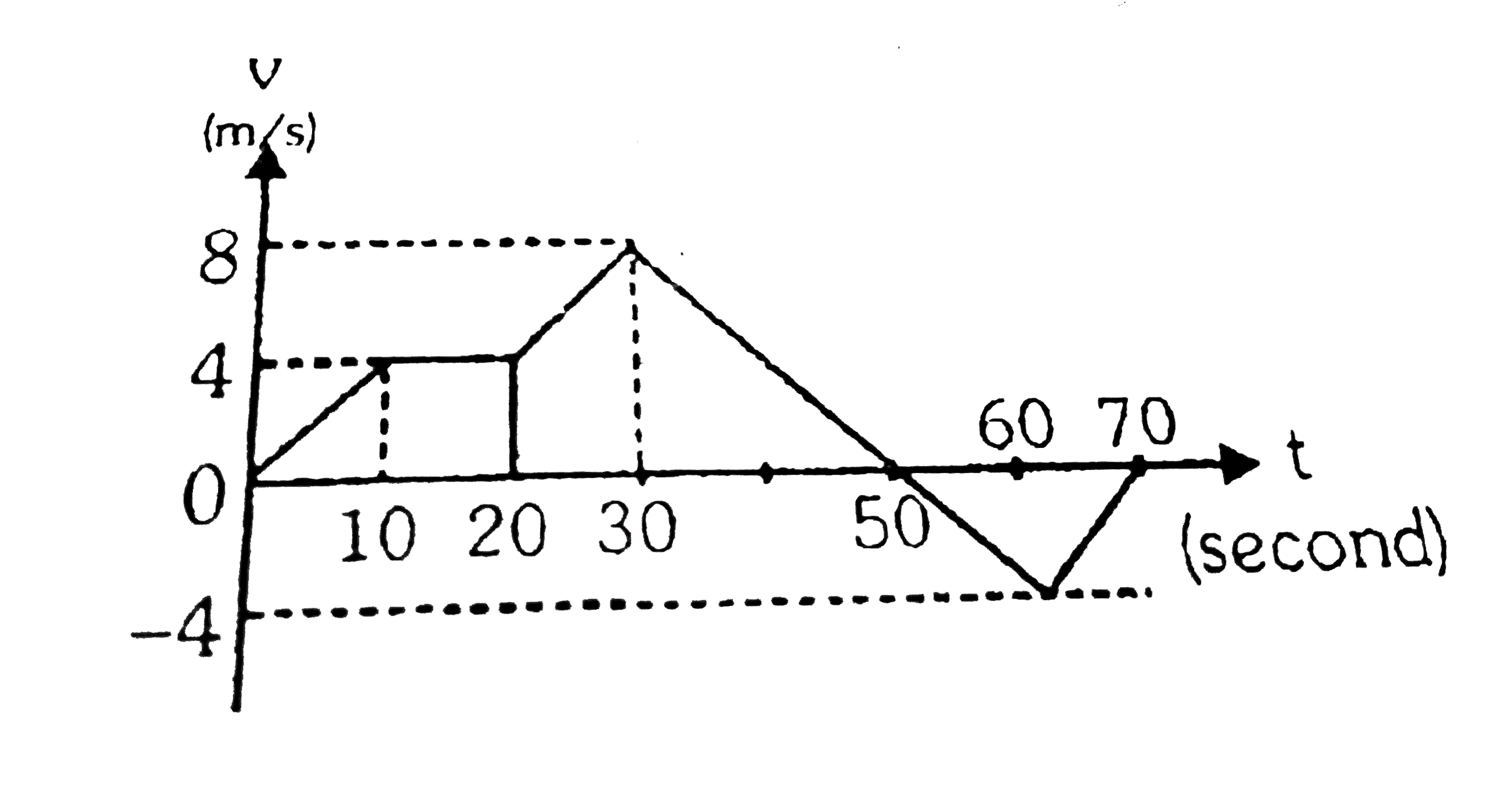
The variation of acceleration (a) with time (t) will be best represented by :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionThe equation of trajectory of an oblique projectile y=√3x−gx22. The angle of projection is
View SolutionThe trajectory of a projectile in a vertical plane is y=sqrt(3)x-2x^(2) . [g=10 m//s^(2)] Angle of projection theta is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]
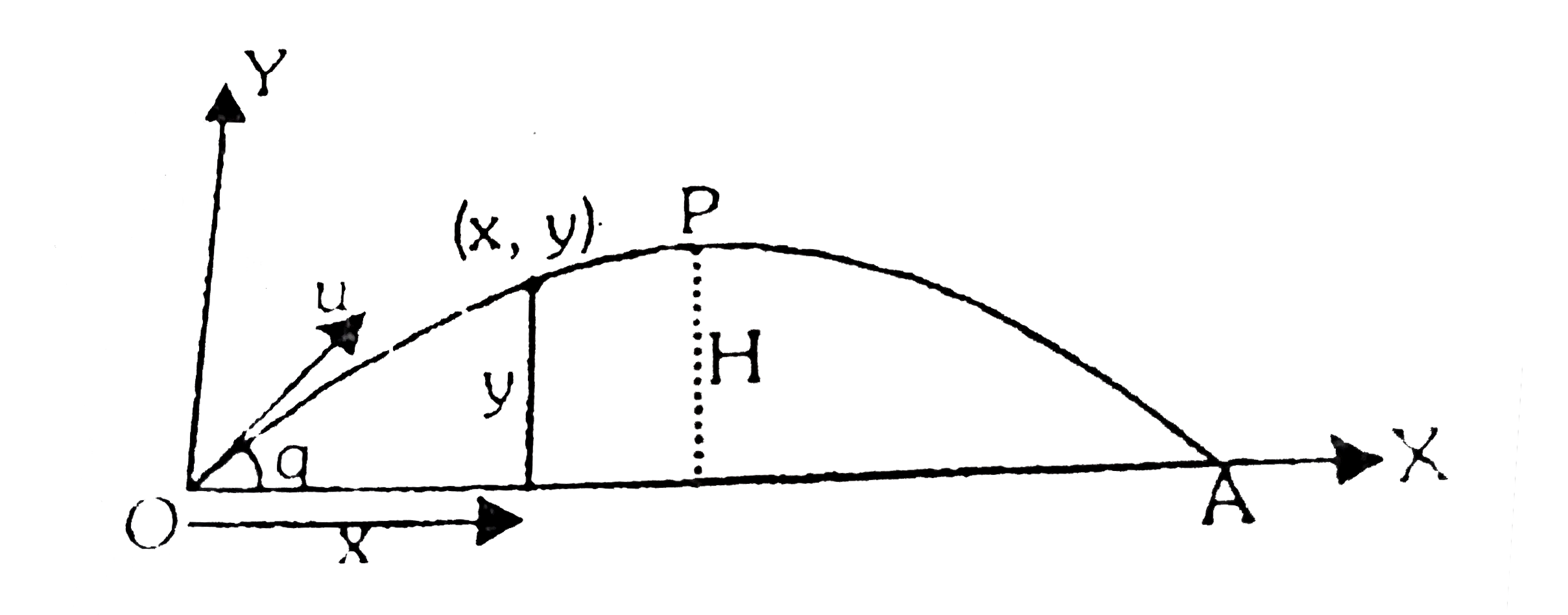
Range OA is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Time of flight of the projectile is :-
View SolutionThe trajectory of a projectile in a vertical plane is y=√3x−2x2. [g=10m/s2]

Radius of curvature of the path of the projectile at the topmost point P is :-
View SolutionRange of a projectile with time of flight 10 s and maximum height 100 m is : (g= -10 m//s ^2)
View SolutionThe equation of a trajectory of a projectile is y=8x-4x^(2) . The maximum height of the projectile is ?
View SolutionThe equation of trajectory of a projectile thrown from a point on the ground is y=(x−x240)m. If g=10ms−2 The maximum height reached is
View SolutionThe equation of trajectory of an oblique projectile y = sqrt(3) x - (g x^(2))/(2) . The angle of projection is
View SolutionThe time of flight of a projectile is 10 s and range is 500m. Maximum height attained by it is [ g=10 m//s^(2) ]
View SolutionRange of a projectile with time of flight 10 s and maximum height 100 m is : (g= -10 m//s ^2)
View Solution
