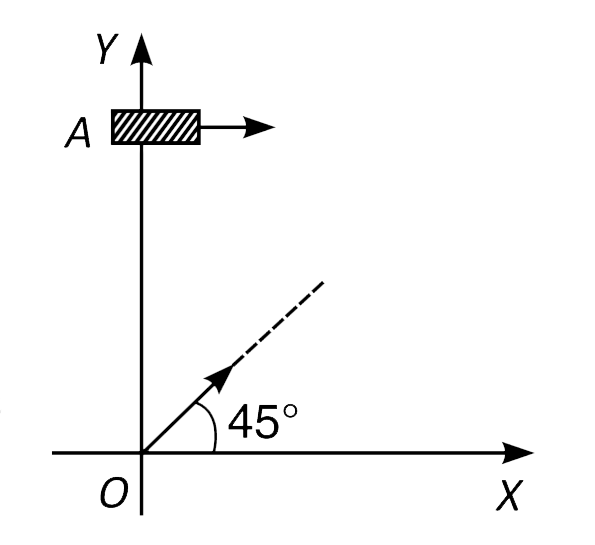
On a frictionless horizontal surface, assumed to be the x-y plane, a small trolley. A is moving along a straight line parallel to the y-axis (see figure) with a constant velocity of (√3−1) m/s. At a particular instant, when the line OA makes an angle of 45∘ with the x-axis, a ball is thrown along the surface from the origin O. Its velocity makes an angle ϕ with the x-axis and it hits the trolley.
(a) The motion of the ball is observed from the frame of trolley. Calculate the angle 0 made by the velocity vector of the ball with the x-axis in this frame.
(b) Find the speed of the ball with respect to the surface, if ϕ−4θ3
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:(i) 45∘ (ii) 2ms−1
(a) From the diagram →VBT makes an angle of 45∘ with the x-axis
(b) Using sine rule
VBsin135∘=VTsin15∘
⇒VB=2m/s

Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Integer Type Question
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - PHY
60 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - MCQ with one or more than one correct Question
1 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
A train is moving along a straight line with a constant acceleration 'a' . A boy standing in the train throws a ball forward with a speed of 10m/s, at an angle of 60(∘) to the horizontal. The boy has to move forward by 1.15m inside the train to catch the ball back at the initial height . the acceleration of the train , in m/s2 , is
View SolutionPosition vector →r of a particle varies with time t accordin to the law →r=(12t2)ˆi−(43t1.5)ˆj+(2t)ˆk, where r is in meters and t is in seconds. Find suitable expression for its velocity and acceleration as function of time.
View SolutionThe coordinate of a particle moving in a plane are given by x(t)=acos(pt)andy(t)=bsin(pt) where a,b(<a) and P are positive constants of appropriate dimensions . Then
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionOn a frictionless horizontal surface , assumed to be the x-y plane , a small trolley A is moving along a straight line parallel to the y-axis ( see figure) with a constant velocity of (sqrt(3)-1) m//s . At a particular instant , when the line OA makes an angle of 45(@) with the x - axis , a ball is thrown along the surface from the origin O . Its velocity makes an angle phi with the x -axis and it hits the trolley . (a) The motion of the ball is observed from the frame of the trolley . Calculate the angle theta made by the velocity vector of the ball with the x-axis in this frame . (b) Find the speed of the ball with respect to the surface , if phi = (4 theta )//(4) .
View SolutionA small cart A starts moving on a horizontal surface, assumed to be x-y plane along a straight line parallel to x-axis (see figure) with a constant acceleration of 4m/s2. Initially it is located on the positive y-axis at a distance 9 m from origin. At the instant the cart starts moving, a ball is rolled along the surface from the origin in a direction making an angle 45° with the x-axis. The ball moves without friction at a constant velocity and hits the cart.
(a) Describe the path of the ball in a reference frame attached to the cart.
(b) Find the speed of the ball.
View SolutionA gun is mounted on a trolley which can move uniformly with speed v m//s along the x -axis. Two shots are find from the origin with the gun making an angle 30^(@) with the horizontal such that in the first case the trolley is moving along the positive x -axis and in the second case moving along the negative x - axis. The respective range of the projectile is 250 m and 200 m , along the x- axis. Find the velocity of the trolley in m//s . (Assume height of the trolley to be negligible)(given g=10m//s^(2) ).
View SolutionA straight line which makes an angle of 60∘ with each of Y and Z-axis, the angle this lines makes with X-axis is
View SolutionA straight line makes an angle of 135∘ with the X-axis and cuts Y-axis at a distance -5 from the origin. The equation of the line is
View Solutionउस सरल रेखा का समीकरण निकालें जो y-अक्ष से 5 का अंतःखंड काटती है तथा x-अक्ष से 45° का कोण बनाती है।
View Solutionएक चोटी ट्रॉली A किसी घर्षणरहित क्षैतिज पृष्ट पर (माना xy तल में ) (√3−1) मी/से के नियत वेग से y अक्ष के समांतर सीधी रेखा में गतिमान है। किसी विशेष समय जब रेखा OA x अक्ष से 45∘ का कोण बनाती है तो मूलबिंदु O से पृष्ठ के अनुदिश एक गेंद फेंकी जाती है। गेंद का वेग x अक्ष से ϕ कोण बनाता है तथा उस वेग से गेंद ट्रॉली से टकराती है।
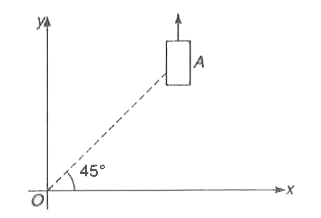
(a) ट्रॉली के फ्रेम से गेंद की गति प्रेक्षित की जाती है । इस फ्रेम में गेंद के वेग सदिश द्वारा x अक्ष से बने कोण θ की गणना कीजिए।
(b) यदि
(b) तो पृष्ट के सापेक्ष गेंद की चाल क्या होगी?
View Solutionयदि एक रेखा x,y और z-अक्ष के साथ क्रमशः 120∘,45∘ और 90∘ के कोण बनाती हैं तो इसकी दिक् -कोज्याएँ ज्ञात कीजिए।
View Solutionதுகள் ஒன்று மாறாத திசைவேகத்துடன் X அச்சுக்கு இணையான நேர்கோட்டின் வழியே இயங்கி கொண்டிருக்கிறது. ஆதியைப் பொருத்து எண்ணளவில் அதன் கோண உ ந்தம்.
View SolutionA particle is moving along a straight line parallel to x-axis with constant velocity. Its angular momentum about the origin
View SolutionA ball is thrown from the origin in the x-y plane with velocity 28.28 m/s at an angle 45∘ to the x-axis. At the same instant a trolley also starts moving with uniform velocity of 10 m/s along the positive x-axis. Initially rear end of the trolley is located at 38 m from the origin. Determine the time and position at which the ball hits the trolley.
View Solution
