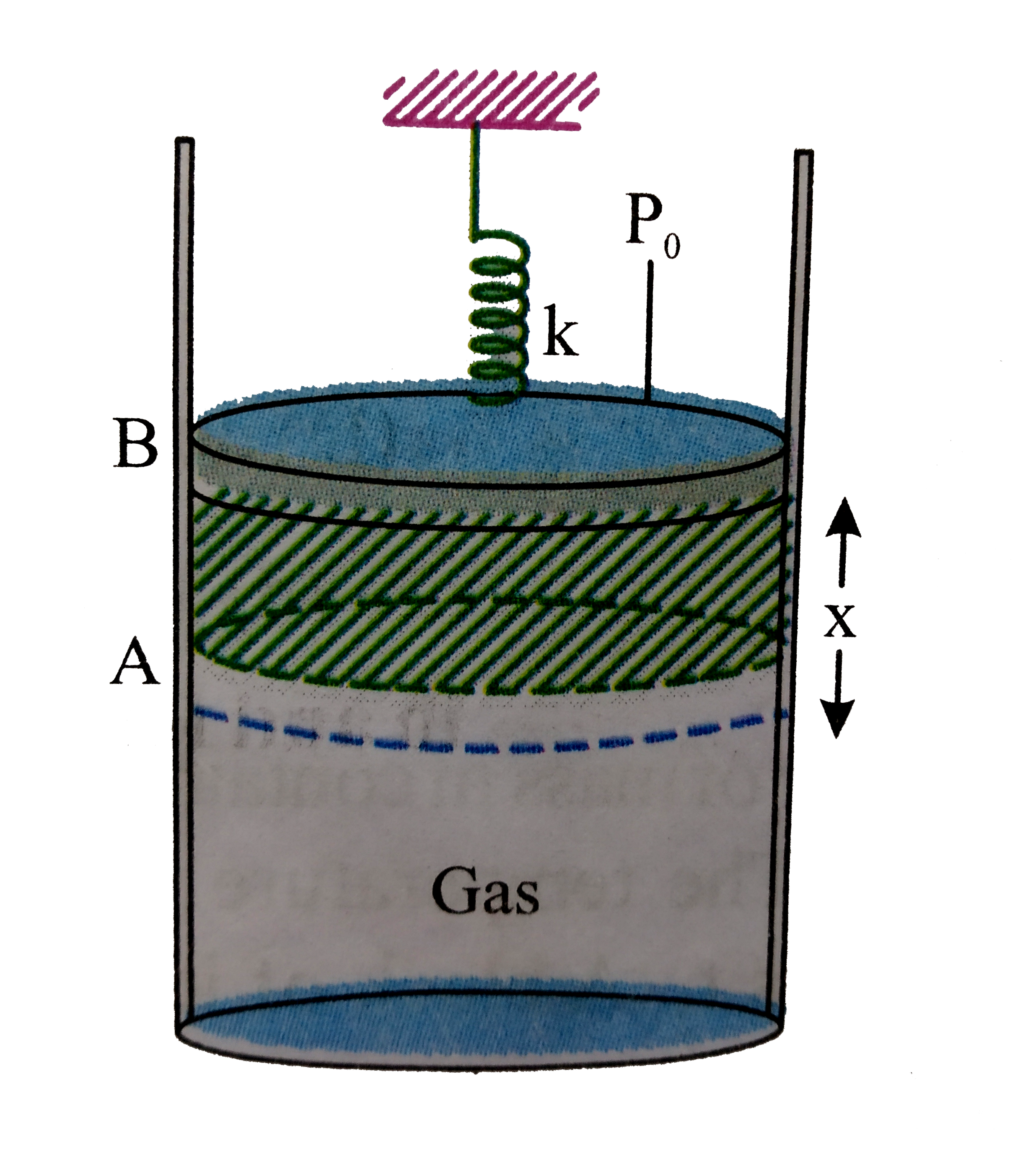
A cylinder of cross-section area. A has two pistons of negligible mass separated by distances l loaded with spring of negligible mass. An ideal gas at temperature T1 is in the cylinder where the springs are relaxed. When the gas is heated by some means its temperature becomes T2 and the springs get compressed by l2 each . if P0 is atmospheric pressure and spring constant k=2P0Al, then find the ratio of T2 and T1 .
_S01_124_Q01.png) Solution in Gujrati
Solution in Gujrati
The correct Answer is:4
P1V1T1=P2V2T2 where V1=lA and V2=2lA and P1=P0 and P2=kxA+P0=2P0⇒T2T1=(P2V2P1V1=4
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
On an X temperature scale, water freezes at −125.0∘X and boils at 375.0∘X. On a Y temperature scale, water freezes at −70.0∘Y and boils at −30.0∘Y. The value of temperature on X-scale equal to the temperature of 50.0∘Y on Y-scale is
View SolutionA triangular plate has two cavities , one square and one rectangular as shown in figure . The plate is heated.
_E01_066_Q01.png)
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionAn ideal monatonic gas is confined in a cylinder by a spring-loaded piston of cross section 8.0×10−3m2.initially the gas is at 300K and occupies a volume of 2.4×10−3m−3 and the sprinng is in its relaxed state. The gas is heated by a small heater until the piston moves out slowly by 0.1m. Calculate the final tenoerature of the gas. The force constant if the spring is 8000Nm−1,and the atmospheric pressure is 1.0×105Nm−2.Htecyl∈derandtheπs→narethermally∈sylated.Theπs→nandthespr∈garemass≤ssandthereisnoictionbetweentheπs→nandthecyl∈der.Neg≤ctanyheat−lossthroughthe≤adwiresoftheheater.Theheat∩acityoftheheatercoilis¬ligib≤.

View Solution2.00 mol of a monatomic ideal gas (U=1.5nRT) is enclosed in an adiabatic, fixed , vertical cylinder fitted with a smooth, light adiabatic piston.the piston is connected to a vertical spring of spring constant 200 N m^(-1) as shown in .the area of cross section of the cylinder is 20.0 cm^(2) . initially, the spring is at its natural length and the temperature of the gas is at its natural length and the temperature of the gas is 300 K. the atmosphere pressure is 100 kPa. the gas is heated sloewly for some time by means of an electric heater so as to move the poston up through 10 cm. find (a) the work done by the gas (b) the final temperature of the gas and (c ) the heat supplied by the heater.
View SolutionIn the arrangement shown in Fig. gas is thermally insulated. An ideal gas is filled in the cylinder having pressure P_(0) (gt atmospheric pressure P_(0) ). The spring of force constant K is initially unstretched. The piston of mass m and area S is frictionless. In equilibrium, the piston rises up by distance x_(0) , then
View SolutionThe air tight and smooth piston of a cylindrical vessel are connected with a string as shown. Initially pressure and temperature of the gas are P_(0) and T_(0) . The atmospheric pressure is also P_(0) . At a later time, tension in the string is (3)/(8) P_(0)A where A is cthe cross-sectional are of the cylinder. at this time, the temperature of the gas has become.
View SolutionTwo mole of an ideal monatomic gas are confined within a cylinder by a mass less spring loaded with a frictionless piston of negligible mass and crossectional area 4×10−3m2. The gas is heated by a heater for some time. During this time the gas expands and does 50J of work in moving the piston through a distance of 0.01m. The temperature of gas increases by 50k.
The force constant of spring is
View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless and frictionless spring loaded piston of cross-sectional area 4 xx 10^(-3)m^(2) . The spring is, initially in its relaxed state. Now the gas is heated by an electric heater, placed inside the cylinder, for some time. During this time, the gas expands and does 50J of work in moving the piston through a distance 0.10m . The temperature of the gas increases by 50K . Calculate the spring constant and the heat supplied by the heater. P_(atm) = 1 xx 10^(5)N//m^(2)R = 8.314 J//mol-K
View SolutionAn adiabatic cylinder of cross section A is fitted with a mass less conducting piston of thickness d and thermal conductivity K. Initially, a monatomic gas at temperature T_(0) and pressure P_(0) occupies a volume V_(0) in the cylinder. The atmospheric pressure is P_(0) and the atmospheric temperature is T_(1) (gt T_(0)) . Find (a) the temperature of the gas as a function of time (b) the height raised by the piston as a function of time. Neglect friction and heat capacities of the container and the piston.
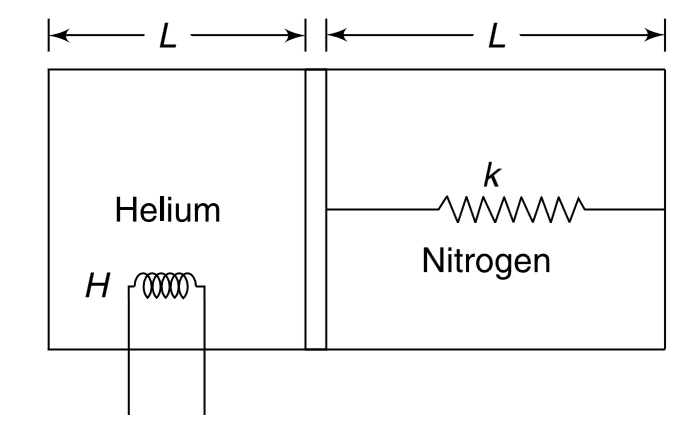
View SolutionAn adiabatic cylinder has length 2 L and cross sectional area A. A freely moving non conducting piston of negligible thickness divides the cylinder into two equal parts. The piston is connected to the right face of the cylinder with an ideal spring of force constant k. The right chamber contains 28 g nitrogen in which one third of the molecules are dissociated into atoms. The left chamber container 4 g helium. With piston in equilibrium and spring relaxed the pressure in both chamber is P0. The helium chamber is slowly given heat using an electric heater (H), till the piston moves to right by a distance 3L4. Neglect the volume occupied by the spring and the heating coil. Also neglect heat capacity of the spring.
(a) Find the ratio of CP and CV for nitrogen gas in right chamber.
(b) Calculate change in temperature of helium.
(c) Calculate heat supplied by the heater.
View SolutionWhen heat is supplied to the gas it expands and displaces piston by L/2 where natural length of springs are L = 1 m. Spring constant K = 100 N/m. Area of piston is 1m2. The pressure of gas in final situation is

View SolutionTwo moles of an ideal monoatomic gas are confined within a cylinder by a massless spring loaded with a frictionless piston of negligible mass and of cross-sectional area 4 xx 10^(-3) m^2 . The springis initially in its relaxed state. Now the gas is heated by a heater for some time. During this time the gas expands and does 50 J of work in moving the piston through a distance of 0.1 m. The temperature of the gas increases by 50 K. Calculate the spring constant and the heat supplied by the heater.
View Solutionएकपरमाणुक आदर्श गैस एक क्षैतिज बर्तन (Horizontal cylinder) में स्प्रिंग युक्त पिस्टन द्वारा बन्द है (दर्शाए चित्रानुसार) | प्रारम्भ में गैस का तापमान T1 दाब p1 तथा आयतन V1 है तथा स्प्रिंग विश्रांत अवस्था में है | अब गैस को बहुत धीरे - धीरे तापमान T2 तक गर्म करने पर दाब p2 तथा आयतन V2 हो जाता है | इस प्रक्रिया में पिस्टन x दुरी तय करता है | पिस्टन एवं बर्तन के मध्य घर्षण को नगण्य मानते हुए, सही कथन है (हैं)

View Solution
