For a ideal monoatomic gas match the following graphs for constant mass in different processes (ρ = Density of gas)
_E01_156_Q01.png) Solution in Gujrati
Solution in Gujrati
P=ρMwRT
For (A):
For ABP∝V⇒TαV2⇒T∝ρ−2
For BCV=constant⇒ρ=constant
For CAP=constant⇒ρT=constant
For (B)
For ABP∝T⇒ρ=constant
For BCT=constant⇒P∝ρ
For CAP=constant⇒ρT=constant
For (C)
For ABP=constant⇒ρT=constant
For BCT=constant⇒P∝ρ
For CAV=constant⇒ρ=constant
For(D)
For ABρ∝T⇒P∝T2
For BCT=constant⇒P∝ρ
For Aρ=constant⇒P∝T
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - ASSERTION-REASON
40 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
Statement-1: A real gas behaves as an ideal gas at high temperature and low pressure .
Statement-2: Liquid state of an ideal gas is impossible.
View SolutionA certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
The initial temperature of ice is
View SolutionA triangular plate has two cavities , one square and one rectangular as shown in figure . The plate is heated.
_E01_066_Q01.png)
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionDuring an experiment, an ideal gas is found to obey a condition (p^2)/(rho) = "constant" . ( rho = density of the gas). The gas is initially at temperature (T), pressure (p) and density rho . The gas expands such that density changes to rho//2 .
View SolutionAn ideal monoatomic gas undergoes a process in which its internal energy U and density ρ vary as Uρ= constant. The ratio of change in internal energy and the work done by the gas is
View SolutionThe density (rho) versus pressure (p) graph of one mole of an ideal monoatomic gas undergoing a cyclic process is shown in figure. Molecular mass of gas is M. (a) Find work done in each process. (b) Find heat rejected by gas in one complete cycle. (c) Find the efficiency of the cycle.
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure.
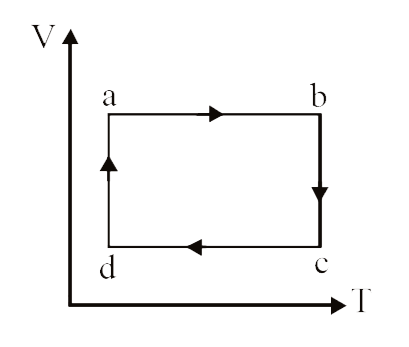
Sum of work done by the gas in process abod is-
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure. Heat is supplied to the gas in process(s)-
View SolutionV-T graph of a process of monoatomic ideal gas is shown in figure. Change in internal energy of the gas is zero in process(s)-
View SolutionAn ideal gas expands following a relation P2ρ= constant, where P = pressure and ρ = density of the gas. The gas is initially at temperature T and density ρ and finally its density becomes ρ3.
(a) Find the final temperature of the gas. (b) Draw the P – T graph for the process.
View SolutionIn the process PV = constant, pressure (P) versus density (ρ) graph of an ideal gas is
View SolutionDuring an experiment, an ideal gas is found to obey a condition p2ρ=constant. (ρ = density of the gas). The gas is initially at temperature (T), pressure (p) and density ρ. The gas expands such that density changes to ρ/2.
View SolutionDuring an experiment, an ideal gas is found to obey a condition P2ρ constant [ρ = density of the gas]. The gas is initially at temperature. T, pressure P and density ρ . The gas expands such that density changes to ρ2
View SolutionDuring an experiment, an ideal gas is found to obey a condition (p^2)/(rho) = "constant" . ( rho = density of the gas). The gas is initially at temperature (T), pressure (p) and density rho . The gas expands such that density changes to rho//2 .
View Solution
