A lead bullet just melts when stopped by an obstacle. Assuming that 25 per cent of the heat is absorbed by the obstacle, find the velocity of the bullet if its initial temperature is 27∘C . (Melting point of lead =327∘C, specific heat of lead =0.03cal/g.∘C, latent heat of fusion of lead =6cal/g,J=4.2J/cal).Solution in Gujrati
The correct Answer is:12.96ms−1
Heat lost = 34(12mv2)
Heat gained = ms(327−27)+mL As heat lost = Heat gained So 34(12mv2)=ms×300+m×L
⇒38v2=0.03×1000×4.2×300+6×1000×4.2
⇒v=12.96m/s
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (B)
15 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - Comprehension Based Questions
66 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
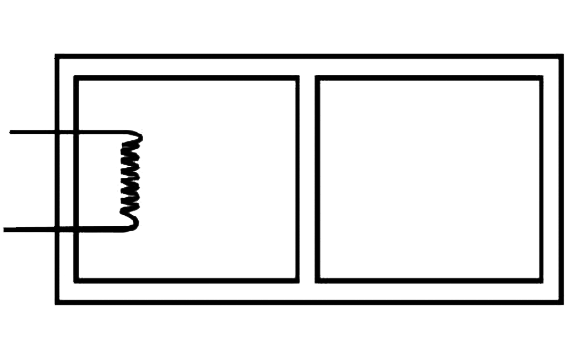
The rectangular box shown in Fig has partition which can slide without friction along the length of the box. Initially each of the two chambers of the box has one mole of a mono-atomic ideal gas (λ=5/3) at a pressure P0, volume V0 and temperature T0. The chamber on the left is slowly heated by an electric heater. The walls of the box and the lead wires of the heater is negligible. The gas in the left chamber expands pushing the partition until the final pressure in both chambers becomes 243P0/32. Determine (i) the final temperature of the gas in each chamber and (ii) the work done by the gas in the right chamber.
View SolutionAn aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionA certain amount of ice is supplied heat at a constant rate for 7 min. For the first one minute the temperature rises uniformly with time. Then it remains constant for the next 4 min and again the temperature rises at uniform rate for the last 2 min. Given Sice=0.5cal/g∘C,Lf=80cal/g.
The initial temperature of ice is
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA lead bullet just melts when stopped by an obstacle. Assuming that 25 per cent of the heat is absorbed by the obstacle, find the velocity of the bullet if its initial temperature is 27^@C . (Melting point of lead= 327^@C , specific heat of lead = 0.03 calories //gm//^@C , latent jeat of fusion of lead= 6calories//gm,J=4.2 joules //calorie ).
View SolutionA lead bullet just melts when stopped by an obstacle. Assuming that 25 per cent of the heat is absorbed by the obstacle, find the velocity of the bullet if its initial temperature is 27∘C. (Melting point of lead=327∘C, specific heat of lead =0.03calories/gm/∘C, latent heat of fusion of lead=6calories/gm,J=4.2joe–s/calorie).
View SolutionDuring the Indo-Pakistan war, a soldier observed that the lead bullet fired by him just melted, when stopped by an obstacle. Assuming that whole of the kinetic energy of bullet got converted into heat energy, calculate the velocity of the bullet. Given that initial temperature of the bullet =47.6∘C. Melting point of lead 321∘C, specific heat of lead =0.3calg−1.∘C−1, latent heat of lead =6calg−1 and J=4.2×107ergcal−1.
View SolutionA lead bullet of mass 50g moving with a velocity of 100ms−1 strikes a target. If 40% of the heat produced is retained by the bullet, calculate the rise in its temperature. Specific heat of lead =0.03calg−1K−1 and J=4.2Jcal−1
View SolutionA lead bullet strikes a target with a velocity of 500ms−1 and the bullet falls dead. Calculate the rise in temperature of the bullet assuming that 40% of the heat produced is used in heating the bullet. Given specific heat of lead =0.03calg−1.∘C−1,J=4.2Jcal−1.
View SolutionWith what velocity must a lead bullet at 50∘C strike against an obstacle in order that the heat produced by the arrest of the motion, is sufficient of melt it, assuming that all the heat produced remains within the bullet?
(Specific heat capacity of lead =31calkg−1K−1, melting point of lead =335∘C, specific latent heat capacity of lead =5370calkg−1K−1 and J=4.2 joules cal−1)
View SolutionA bullet of lead melts when stopped by obstacle. Assuming that 25 per cent of the heat is absorbed by the osbtacle, find the velocity of the bullet if its initial temperature is 27^(@)C . (Melting point of lead 327^(@)C , specific heat capacity of lead =30 cal kg^(-1)K^(-1) specific latent heat of fusion of lead =6000 cal kg^(-1) and J=4.2 joules cal^(-1) )
View SolutionA hunter fired a metallic bullet of mass 'm' kg from a gun towards an obstacle and it just melts when it is stopped by the obstacle. The initial temperature of the bullet is 300K. If 1th4 of heat is absorbed by the obstacle, then the minimum velocity of the bullet is
[Melting point of bullet =600K,
Specific heat of bullet =0.3cal g−1.0C−1,
Latent heat of fusion of bullet =6calg−1].
View SolutionThe temperature of a piece of lead is 27^(@)C . Find out the minimum velocity of its impact with a wall so that it melts completely. Suppose 58% of the heat generated is dissipated. Given, J = 4.2 J cdot cal^(-1) , melting point, specific heat and latent heat of fusion of lead are 327^(@)C, 0.03 cal cdot g^(-1) cdot^(@)C^(-1) and 5 cal cdot g^(-1) , respectively.
View SolutionA lead bullet melts on hitting a fixed target. What will be the minimum speed of the bullet, if it is assumed that the heat produced is retained entirely by the bullet? Initial temperature of the bullet = 47.6∘C, specific heat of lead = 0.03cal⋅g−1⋅∘C−1, melting point of lead = 327∘C, latent heat of fusion of lead = 6cal⋅g−1,J=4.2×107erg⋅cal−1.
View Solution
