A non-conducting cylindrical vessel of length is placed horizontly & is divided into three parts by two easily moving piston having low thermal conductivity as shown in figure. These parts contains He and gas at initial temp. and respectively. If initial length and pressure of each part are l and respectively. calculate final pressure and length of each part . Use :
_E01_301_Q01.png) Solution in Gujrati
Solution in Gujrati
The correct Answer is:
For the gas
For the He gas
For the gas
&
For the entire system
_E01_301_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)
58 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
An aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionA vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rorational kinetic energy per O2 molecules to that per N2 molecules is
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionA container of volume 4V_(0) made of a perfectly non - conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non - conducting and upper half is purely conducting. The right side of the wall is divided into equal parts ( initially 0 by means of a massless non - conducting piston free to move as shown . Section A constains 2 mol of a gas while the section B and C contain 1 mol each of the same gas ( gamma = 15. ) at pressure P_(0) . The heater in left part is switched on till the final pressure in section C becomes 125//27 P_(0) . Calculate Final temperature in part A .
View SolutionA container of volume 4V0 made of a perfectly non− conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non− conducting and upper half is purely conducting. The right side of the wall is divided into equal parts ( initially 0 by means of a massless non− conducting piston free to move as shown . SectionA constains 2mol of a gas while the section B and C contain 1mol each of the same gas (γ=15.) at pressure P0 . The heater in left part is switched on till the final pressure in section C becomes 125/27P0. Calculate
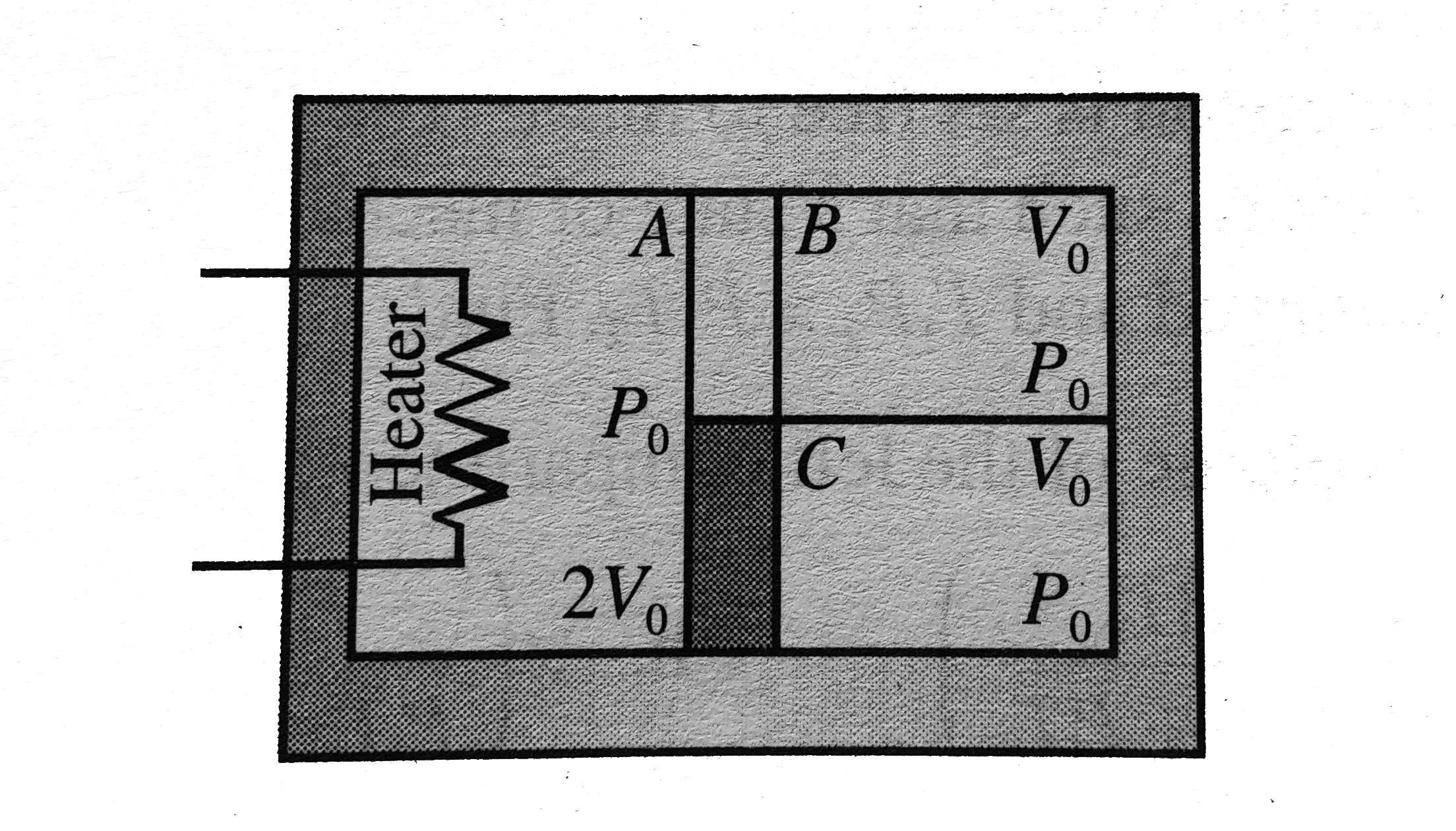
Final temperature in part C.
View SolutionA container of volume 4V0 made of a perfectly non− conducting material is divided into two equal parts by a fixed rigid wall whose lower half is non− conducting and upper half is purely conducting. The right side of the wall is divided into equal parts ( initially 0 by means of a massless non− conducting piston free to move as shown . Section A contains 2mol of a gas while the section B and C contain 1mol each of the same gas (γ=15.) at pressure P0 . The heater in left part is switched on till the final pressure in section C becomes 125/27P0. Calculate
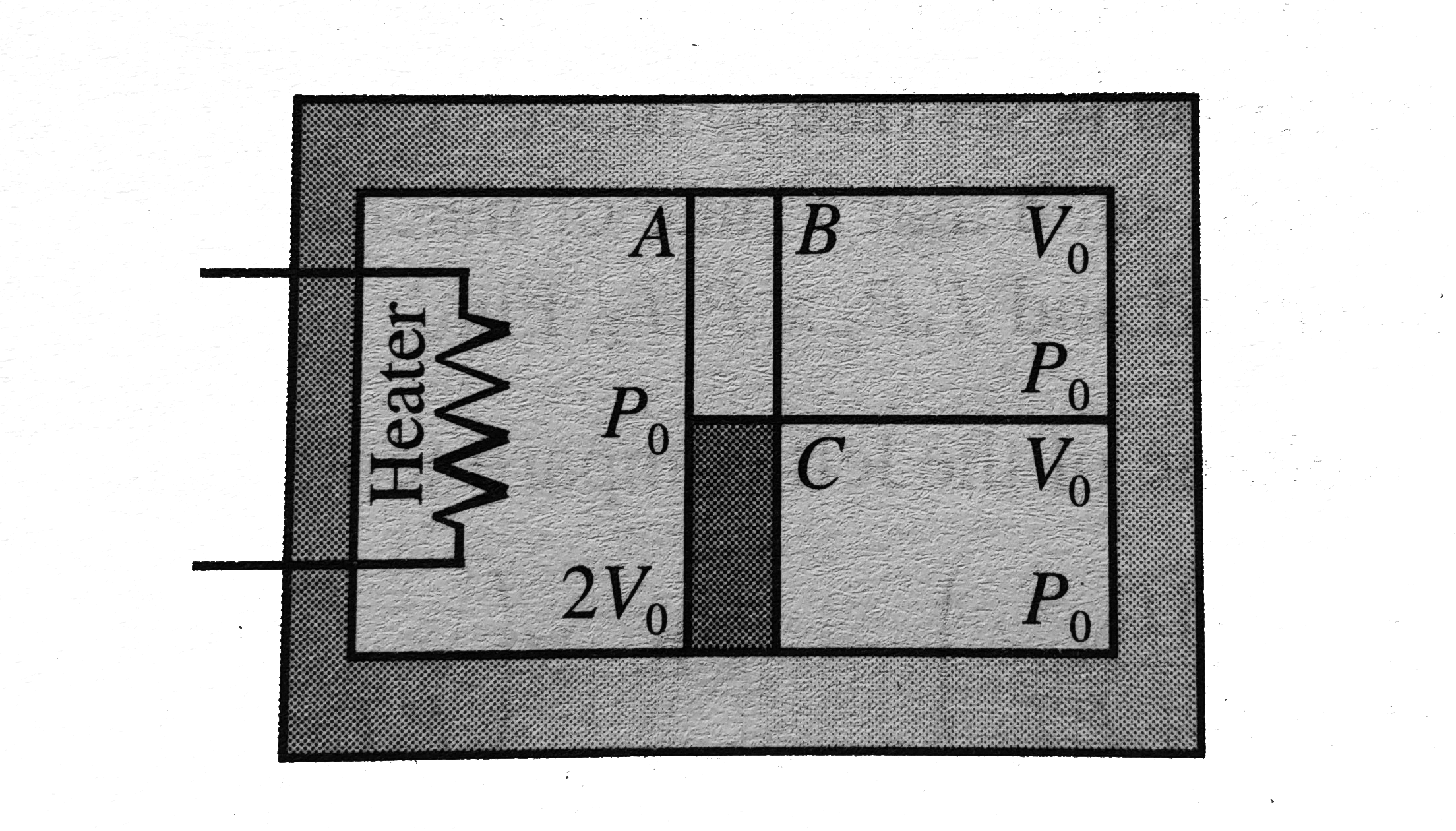
The heat supplied by the heater.
View SolutionTwo pistons having low thermal conductivity divide an adiabatic container in three equal parts as shown An ideal gas is present in the three parts AB&C having initial pressures as shown and same temperatures Now the pistons are releasef Then the final equilibrium length of part A after long time will be
View SolutionThe base of a triangle is divided into three equal parts. If θ1,θ2,θ3 be thw angles subtended by these parts at the vertex, then prove that
(cotθ1+cotθ2)(cotθ2+cotθ3)=4cosec2θ2
View SolutionTwo materials having coefficients of thermal conductivity ‘3 K’ and ‘K’ and thickness ‘d’ and ‘3 d’, respectively, are joined to form a slab as shown in the figure. The temperatures of the outer surfaces are theta_(2) and theta_(1) respectively, (theta_(2) gt theta_(1)) The temperature at the interface is:
View SolutionThree bars each of area of cross section A and length L are connected in series as shown in the figure. Thermal conductivities of their materials are K, 2K and 1.5K. If the temperatures of free end of first and the last bar are 200^(@)C and 18^(@)C . The value of theta_(1) and theta_(2) are (in steady state):
View SolutionA thin rod having length L_(0) at 0^(@)C and coefficient of linear expansion alpha has its two ends maintained at temperature theta_(1) and theta_(2) respectively. Find its new length.
View SolutionFigure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.

View SolutionTwo materials having coefficients of thermal conductivity '3k' and 'k' and thickness 'd' and '3d' respectively, are joined to form a slab as shown in the figures. The temperatures of the outer surfaces are θ2 and θ1 respectively (θ2>θ2). The temperature at the interface is :
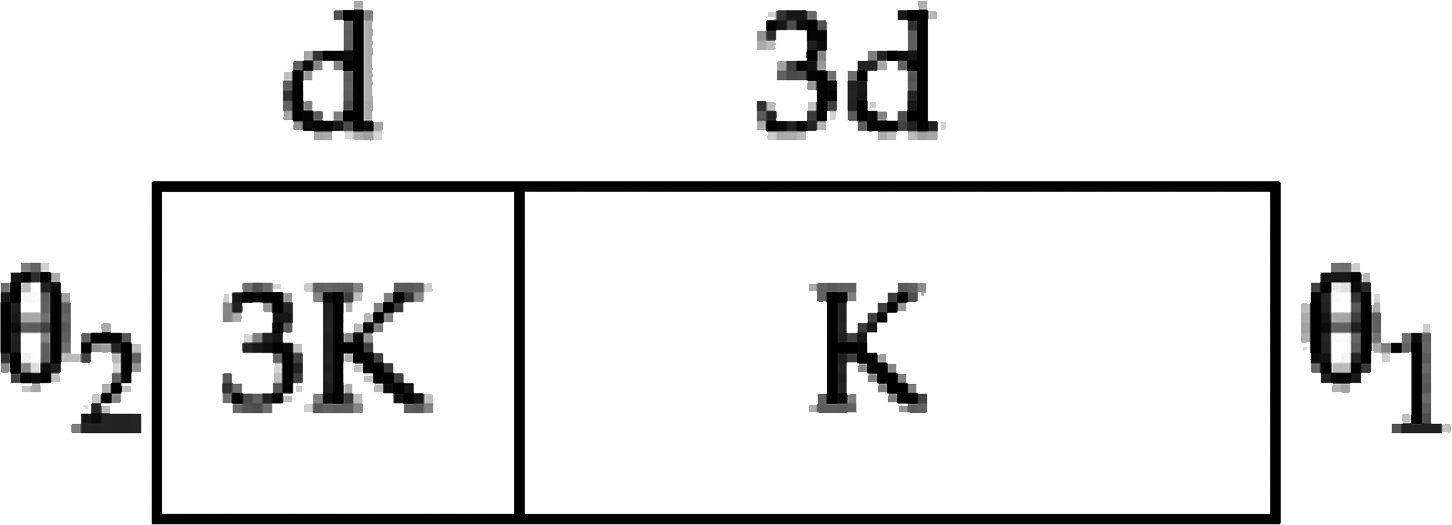
View SolutionThe base of a triangle is divided into three equal parts. If θ1,θ2,θ3 be thw angles subtended by these parts at the vertex, then prove that
(cotθ1+cotθ2)(cotθ2+cotθ3)=4cosec2θ2
View Solution
