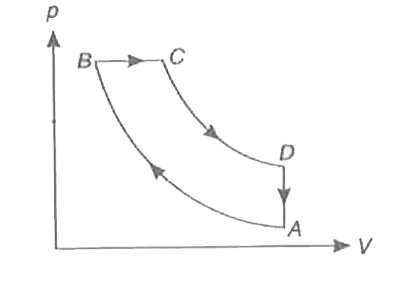
One mole of a diatomic ideal gas (γ=1.4) is taken through a cyclic process starting from point A. The process A→B is an adiabatic compression, B→C is isobaric expansion, C→D is an adiabatic expansion, and D→A is isochoric. The volume ratios are VA/VB=16andVC/VB=2 and the temperature at A is TA=300K. Calculate the temperature of the gas at the points B and D.Solution in Gujrati
The correct Answer is:TB=909K,TD=791.4K,61.4%
Let VB=V0
Process A→B
TAVγ−1A=TBVγ−1
⇒TB=909K
Process B→C VBTB=VCTC⇒TC=7272K
Process C→D:TCVγ−1C=TDVγ−1D⇒TD=5511.15K
Heat flow
Process A→B QAB=0
Process D→A QDA=nCvΔT
=1(52R)(TA−TD)
= −108313.753J
∴ Efficiency , η=work output Heat output=Qin−QoutQin
=(1−QoutQin)×100%=(1−108313.753185156.937)×100%η=41.50%
_E01_292_S01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (A)
73 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 05 (B)
58 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE - 04 (A)
48 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
An aluminium sphere of 20cm diameter is heated from 0∘C to 100∘C. Its volume changes by (given that the coefficient of linear expanison for aluminium (αAl=23×10−6/0C)
View SolutionA vessel contains a mixture of one mole of oxygen and two moles of nitrogen at 300K. The ratio of the average rorational kinetic energy per O2 molecules to that per N2 molecules is
View SolutionTwo rods each of length L2 and coefficient of linear expansion α2 each are connected freely to a third rod of length L1 and coefficient of expansion α1 to form an isoscles triangle. The arrangement is supported on a knife-edge at the midpoint of L1 which is horizontal. what relation must exist between L1 and L2 so that the apex of the isoscles triangle is to remain at a constant height from the knife edge as the temperature changes ?
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionOne mole of a monoatomic ideal gas is taken through the cycle shown in Fig: AtoB : adiabatic expansion BtoC : cooling at constant volume CtoD : adiabatic compression DtoA : heating at constant volume The pressure and temperature at A,B,etc. are denoted by P_A, T_A,P_B,T_B etc. respectively. Given that T_A=1000K , P_B=(2//3)P_A and P_C=(1//3)P_A , calculate the following quantities: (i) The work done by the gas in the process AtoB (ii) The heat lost by the gas in the process BtoC . (iii) The temperature T_D . [Given : (2//3)^(2//5)=0.85 ]
View SolutionOne mole of a diatomic ideal gas (gamma=1.4) is taken through a cyclic process starting from point A. The process AtoB is an adiabatic compression, BtoC is isobaric expansion, CtoD is an adiabatic expansion, and DtoA is isochoric. The volume ratios are V_A//V_B=16 and V_C//V_B=2 and the temperature at A is T_A=300K . Calculate the temperature of the gas at the points B and D and find the efficiency of the cycle.
View SolutionA monoatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in figure. The volume ratios are VBVA=2andVDVA=4. If the temperature TA at A is 27∘C.
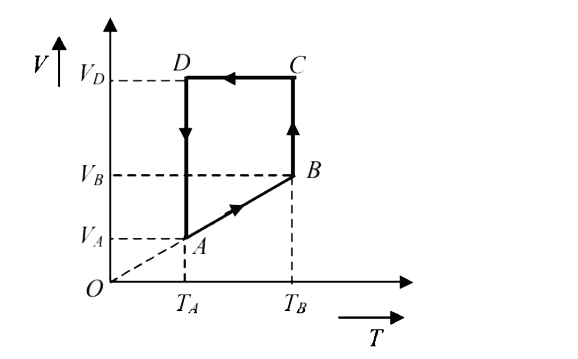
Calculate,
(a) the temperature of the gas at point B,
(b) heat absorbed or released by the gas in each process,
(c) the total work done by the gas during the complete cycle. Express your answer in terms of the gas constant R.
View SolutionAn ideal mono atomic gas is taken through the cyclic process shown in fig. Linear expansion from A to B following by adiabatic compression back to original state
View SolutionAn ideal gas at initial temperature 300 K is compressed adiabatically (γ=1.4) to (116)th of its initial volume. The gas is then expanded isobarically to double its volume. Then final temperature of gas round to nearest integer is:
View SolutionTwo adiabatic expansions of n mole of same gas are shown. If VBVA=VDVC×12 then TC/TD is :

View Solutionएक मोल द्विपरमाणुक आदर्श गैस (γ=1.4) को बिन्दु A से प्रारम्भ होने वाले एक चक्रीय प्रक्रम में ले जाया जाता है | प्रक्रम A→B रुद्धोष्म संपीडन है, B→C समदाबी प्रसार है, C→D रुद्धोष्म प्रसार है तथा D→A समायतनिक प्रक्रम है | आयतन अनुपात VA/VB=16 व VC/VB=2 है तथा बिन्दु A पर ताप TA=300 केल्विन है | बिन्दुओं B व D पर गैस के ताप की गणना कीजिए तथा चक्रीय प्रक्रम की दक्षता ज्ञात कीजिए |
View SolutionAn ideal gas at initial temperature 300 K is compressed adiabatically ( gamma = 1.4 ) to (1/16)^(th) of its initial volume. The gas is then expanded isobarically to double its volume. Then final temperature of gas round to nearest integer is:
View SolutionAn ideal gas at initial temperature 300 K is compressed adiabatically (γ=1.4) to (116)th of its initial volume. The gas is then expanded isobarically to double its volume. Then final temperature of gas round to nearest integer is:
View SolutionA monatomic ideal gas of two moles is taken through a cyclic process starting from A as shown in the figure. The volume ratios are (V_B//V_A) = 2 and (V_D//V_A ) = 4 . If the temperature T_A at A is 27^@ C, calculate, a) The temperature of the gas at point B, b) Heat absorbed or released by the gas in each process. c) The total work done by the gas during the complete cycle. Express your answer in terms of the gas constant R.
View Solution
