In figure , L is half part of an equiconvex glass lens (μ=1.5) whose surfaces have radius of curvature R =40cm and its right surface is silvered . Normal to its principal axis a plane mirror M is placed on right of the lens . Distance between lens L and mirror M is b. A small object O is placed on left of the lens such that there is no parallax between final images formed by the lens and mirror. If transverse length of final image formed by lens is twice that of image formed by the mirror , calculate distance'a' in cm between lens and object.
_S01_072_Q01.png) Solution in Gujrati
Solution in Gujrati
Distance of image of object O from plane mirror = a+b . Since , there is no parallax between the image formed by the silvered lens L and plane mirror M, therefore, two images are formed at the same point . Distance of image = (a+2b) behind lens. Since , length of image formed by L is twice the length of image formed by the mirror M and length of image formed by a plane mirror is always equal to length of the object , therefore , transverse magnification produced by the lens L is equal to 2 . Since, distance of object from L is a therefore, distance of image from L must be equal to 2a.
∴(a+2b)=2a⇒b=a2
The silvered lens L may be assumed as a combination of an equi-convex lens and a concave mirror placed in contact with each other co-axially as shown in figure.
_S01_072_S01.png)
Focal length of convex lens f1 is given by 1f1=(μ−1)(1R1−1R2)⇒f1=40cm
For concave mirror focal length , fm=R2=−20cm
The combination L behaves like a mirror whose equivalent focal length F is given by
1F=1fm−2f1⇒F=−10cm
Hence , for the combination u=-a , v=+2a , F=-10cm
Using mirror formula , 1v+1u=1F⇒a=5cm
_S01_072_Q01.png)
Topper's Solved these Questions
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -01
65 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - EXERCISE -02
82 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- CURRENT ELECTRICITYBOOK - ALLEN CHAPTER - CURRENT ELECTRICITYEXERCISE - EX.II
66 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - EXERCISE 4
9 Videos
Similar Questions
On an X temperature scale, water freezes at −125.0∘X and boils at 375.0∘X. On a Y temperature scale, water freezes at −70.0∘Y and boils at −30.0∘Y. The value of temperature on X-scale equal to the temperature of 50.0∘Y on Y-scale is
View SolutionA triangular plate has two cavities , one square and one rectangular as shown in figure . The plate is heated.
_E01_066_Q01.png)
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionIn the Bohr's model of hy drogen atom, the electron moves around the nucleus in a circular orbit of radius 5×10−11m. Its time period is 1.5×10−16s. The current associated with the electron motion is:-
View SolutionAssertion : The difference in the value of acceleration due to gravity at pole and equator is proportional to square of angular velocity of earth.
Reason : the value of acceleration due to gravity is minimum at the equator and maximum at the pole.
View SolutionOn a horizontal plane mirror, a thin equiconvex lens of glass is placed and when the space between the lens and mirror is filled with a liquid, an object held at a distance D which is 30cm vertically above the lens is found to coincide with its own image as shown in Figure. If equiconvex lens of glass has refractive index μ=1.5 and radius of curvature R=20cm then find refractive index of the liquid.

View SolutionAs shown in figure. L is half part of an equiconvex lens (mu=1.5) whose surface have radius of curvature R=40cm and its right surface in silvered. Normal to principal axis, a plane mirror M is placed on the right of lens. A small object O is placed on left of the lens such that there is no parallax between final images formed by the lens and mirror. If transverse length of final image formed by the lens is twice that of image formed by the mirror. Calculate distance a between lens and object and distance b .
View SolutionA thin equiconvex glass lens (mu_(1) = 1.5) of radius of curvature 'R' and a thin plano-concave lens (mu_(2) = 1.4) are kept in contact and the plane surface is silvered. This lens system is placed in air. When a point object is placed at a distance 20 cm from the lens system on its principal axis, the image formed by the lens system coincides with the object. Then the value of radius of curvature 'R' is
View SolutionAn thin Plano - convex glass lens (mu=1.5) has its plane surface silvered and R is the radius of curvature of curved part, then which of the following ray diagram is true for an object placed at O ? (O is at a distance of 2 R from the lens)
View Solutionएक काँच का पतला समतलोत्तल जिसके काँच का अपवर्तनांक μ=3/2 है तथा जिसकी वायु में फोकस दूरी 0.3 मी है, जल (μ=4/3) से भरे टैंक के एक सिरे पर बने मुख में सील किया गया है | लेंस के दूसरी ओर टैंक के भीतर टैंक की दीवार पर लेंस की अक्ष के लम्बवत एक समतल दर्पण रखा गया है | लेंस तथा दर्पण के बीच अंतराल 0.8 मी है | टैंक के बाहर लेंस की अक्ष पर लेंस से 0.9 मी की दूरी पर एक छोटी वस्तु रखी गई है | निकाय द्वारा बने वस्तु के प्रतिबिम्ब की स्थिति( लेंस के सापेक्ष ) ज्ञात कीजिए |
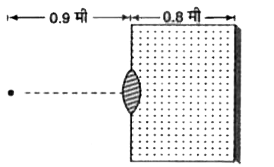
View SolutionA thin equiconvex lens of glass of refractive side of 3/2 and of focal length 0.3 m is sealed into an opening at end of a tank filled with water (p=4/3). on the opposite side of the lens a mirror is placed inside the tank with the tank wall perpendicular to the sense axis as shown in figure The separation between the lens and mirror is 0.8 m. A small object is placed outside the tank is front of the lens, at a distance of 0.9 m from the lens along its axis. Find the position (relative to the lens) of the image of the object formed by the system.
View SolutionThere is a glass (mu=1.5) biconvex lens of radius of curvature 5 cm and thickness of the lens is also 5 cm. An object is placed at a distance 20 cm from the front surface of lens. Locate its final image.
View SolutionA thin plano-convex lens acts like a concave mirror of focal length 0.2 m when silvered from its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the lens will be
View SolutionA thin plano -convex lens acts like a concave mirror of focal length 0.2 m when silvered from its plane surface. The refractive index of the material of the lens is 1.5. The radius of curvature of the convex surface of the less will be
View Solutionएक उभयोत्तल लेन्स के काँच का अपवर्तनांक μ=1.5 एवं इसके प्रत्येक पृष्ठ की वक्रता त्रिज्या 0.2 मीटर है लेन्स की क्षमता है
View Solution10 cm वक्रता त्रिज्या का एक समतल उत्तल लेंस (μ=1.5) की समतल सतह को रजित कर देते हैं। तो रजित करने के बाद लेंस की फोकस दूरी होगी :
View Solution
