A particle is oscillating in a stright line about a centre of force O, towards which when at a distance x the force is mn2x where m is the mass, n a constant. The amplitude is a=15cm. When a distance a√32 from O, find the new amplitude.Solution in Gujrati
The correct Answer is:A, C
As v=ω√a2−x2 so vi=n√a2−3a24=na2
and v2=32na=−n√A2−3a24
⇒A=√3a=15√3cm
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]
104 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)
3 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.

View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle A can be written as-
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA particle starts from a point P at a distance of A//2 from the mean position O and travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of the motion of particle is
View SolutionA particle performs SHM of amplitude A along a straight line .When it is a distance √32A from mean position its kinetic energy gets increase by on amount 12mω2A2 due to an implusive force. Then its new amplitude because
View SolutionA particle starts from a point P at a distance of A/2 from the mean position O& travels towards left as shown in the figure. If the time period of SHM, executed about O is T and amplitude A then the equation of motion of particle is :
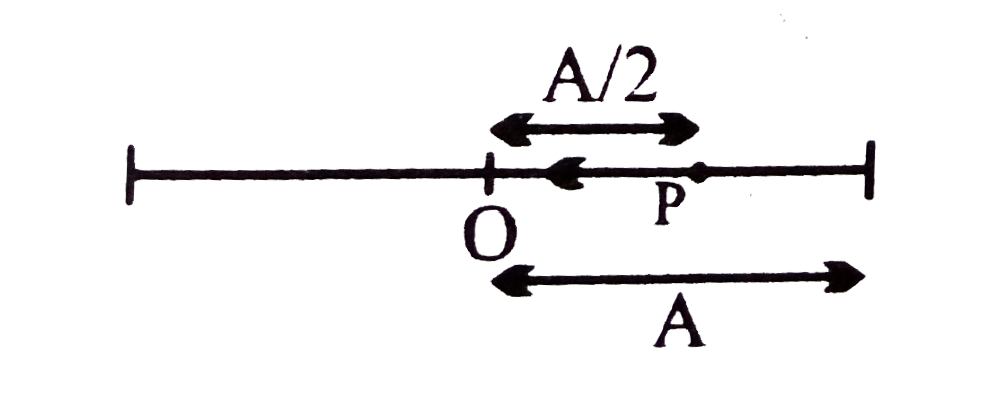
View SolutionWhen 'n' number of particles of masses m are at distances x_1 =a, x_2 =ar, x_3=ar^2…x_n = ar^n ,units from origin on the X-axis, then find the distance of centre of mass of the system from origin.
View SolutionA particle of mass m is executing oscillations about the origin on the x-axis, it's potential energy is U(x)=k|x|^(2) , where k is a positive constant, if the amplitude of oscillation is a, then it's time period T is
View SolutionA particle is oscillating in a stright line about a centre of force O, towards which when at a distance x the force is mn2x where m is the mass, n a constant. The amplitude is a=15cm. When a distance a√32 from O, find the new amplitude.
View SolutionA particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA linear harmonic oscillator of force constant 10^(6) N//m and amplitude 2 cm has
View SolutionA body of mass 15 g oscillates about a fixed point with a SHM of amplitude 8cm . If the body is attracted towards the fixed point, when at a distance of 4 cm from it with a force equal to the weight of 10 g , the period of oscillation of the mass about the fixed point is
View SolutionA body of mass 15 g oscillates about a fixed point with a SHM of amplitude 8cm . If the body is attracted towards the fixed point, when at a distance of 4 cm from it with a force equal to the weight of 10 g , the period of oscillation of the mass about the fixed point is
View SolutionThe force constant of a particle of mass 1kg is SHM of amplitude 4cm is 100N//m when particle is at mean position at t = 0 then find maximum speed.
View Solution
