A small ring of mass m1 is connected by a string of length l to a small heavy bob of mass m2. The ring os free to move (slide) along a fixed smooth horizontal wire. The bob is given a small displacement from its equilibrium position at right angles to string. Find period of small oscillations.
_E01_106_Q01.png)
Solution in Gujrati
The correct Answer is:A, B
Centre of mass will be at rest as there is no external
So effective length
leff=(m1m1+m2)l
t=2π√leffg=2π√m1l(m1+m2)g
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [B]
104 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Comprehension Base Questions (5)
3 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
In the arrangement shown in figure, pulleys are light and spring are ideal. K1, k2, k3and k4 are force constant of the spring. Calculate period of small vertical oscillations of block of mass m.
View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionTwo particles A and B are performing SHM along x and y-axis respectively with equal amplitude and frequency of 2cm and 1Hz respectively. Equilibrium positions of the particles A and B are at the coordinates [3cm,0] and (0,4cm) respectively. At t=0,B is at its equilibrium position and moving towards the origin, while A is nearest to the origin and moving away from the origin-
Equation of motion of particle A can be written as-
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionA small ball B of mass m is suspended with light inelastic string of length L from a block A of same mass in which can move on smooth horizontal surface as shown in the figure. The ball is displaced by angle θ from equilibrium position and then released.
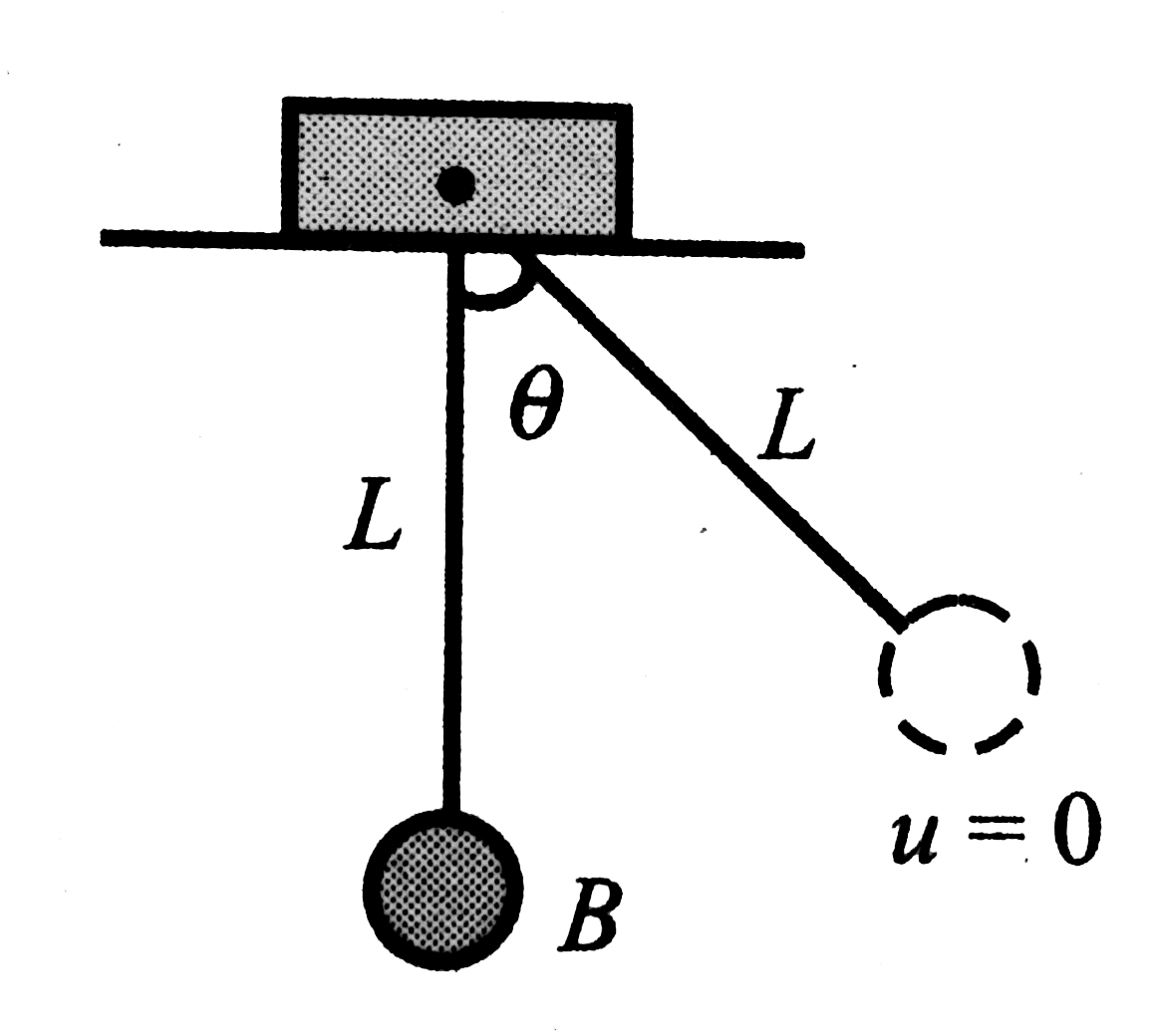The displacement of centre of mass of A+B system till the string becomes vertical is
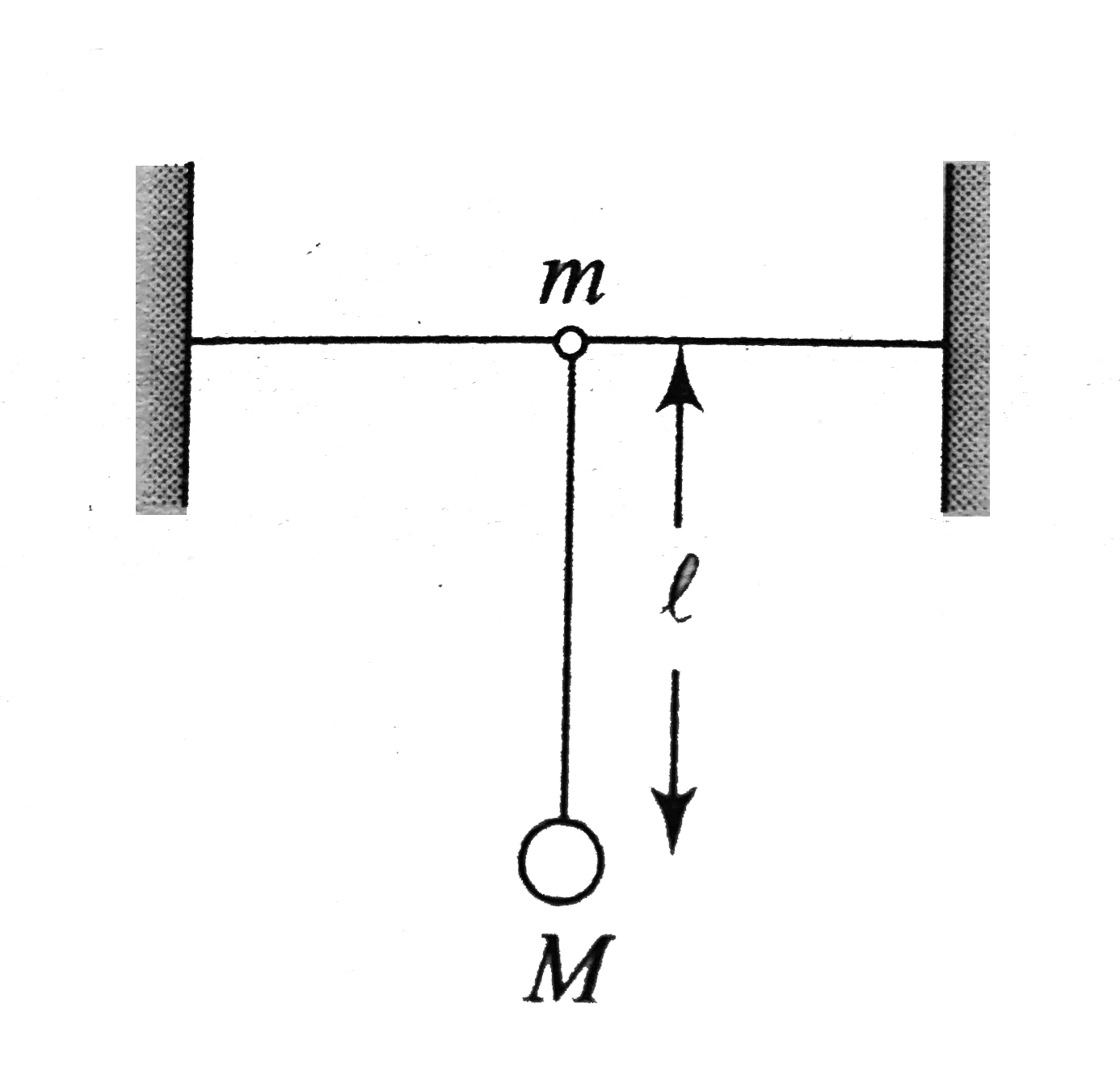
View SolutionA smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
View SolutionThe string of a simple pendulum replaced by a uniform rod of length L and mass M while the bob has a mass m . It is allowed to make small oscillation. Its time period is
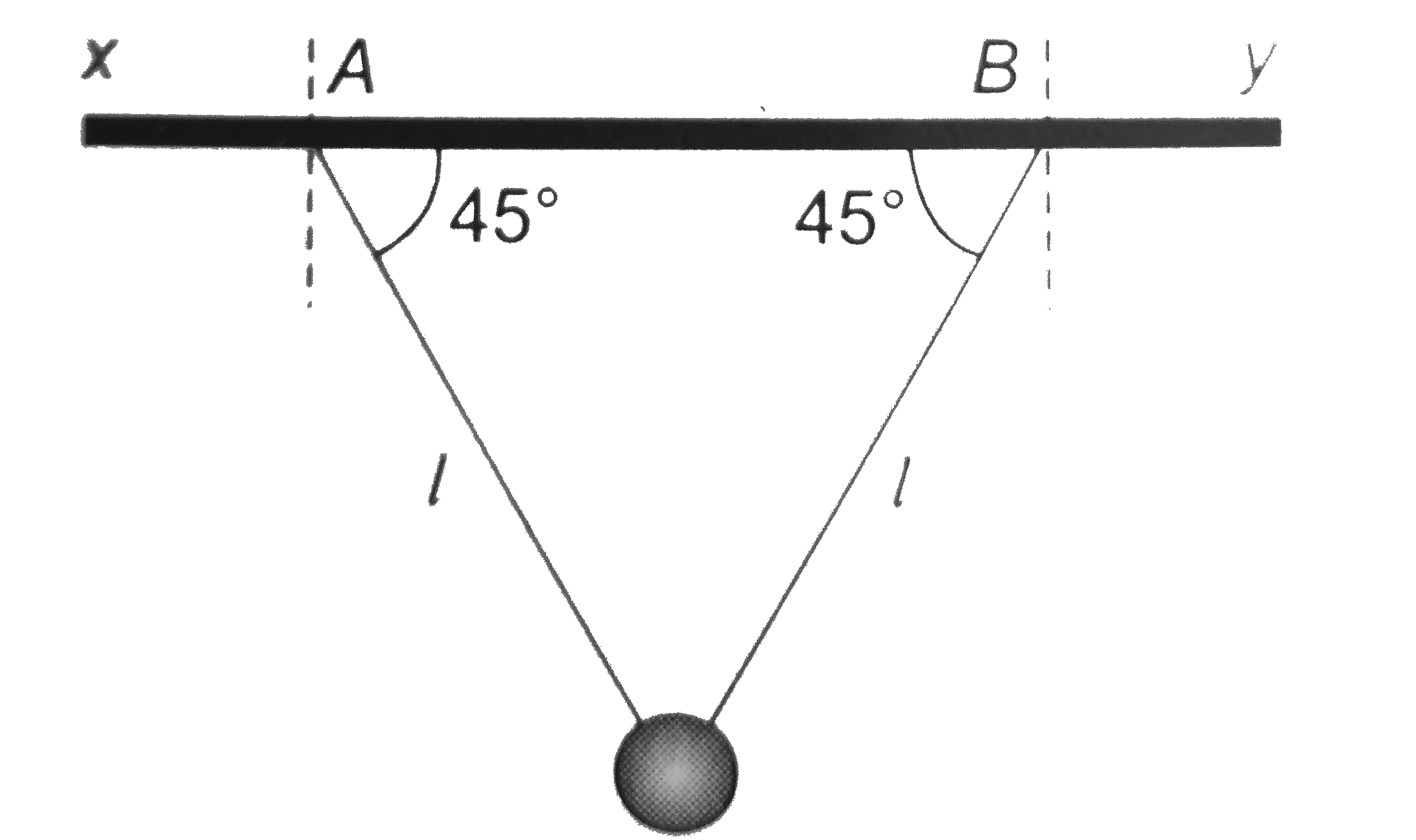
View SolutionTwo light strings, each of length l are fixed at points A andB on a fixed horizontal and xy A small are making angle 45∘ with the bob if the bob is displaced normal to the plane of the string and released then period of the resulting small oscillation will be
View SolutionA bob of mass M is hung using a string of length l . A mass m moving with a velocity u pierces thorugh the bob and emerges out with velocity (u)/(3) horizontally. The frequency of small oscillations of the bib, considering A as amplitude is,
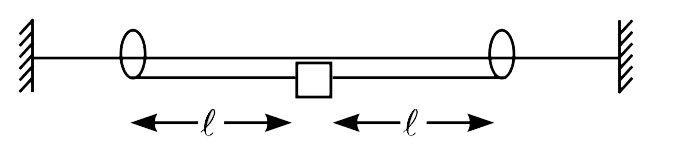
View SolutionTwo small rings each of mass ‘m’ are connected to a block of same mass ‘m’ through inextensible light strings. Rings are constrained to move along a smooth horizontal rod. Initially system is held at rest (as shown in figure) with the strings just taut. Length of each string is ‘l’. The system is released from the position shown. Find the speed of the block (v) and speed of the rings (u) when the strings make an angle of theta=60^(@)withvertical.(Takeg = 10 m//s^2)
View SolutionTwo small metal balls of different mass m_(1) and m_(2) are connected by strings of equal length to a fixed point. When the balls are given equal charges, the angles that the two strings make with the vertical are 30^(@) and 60^(@) , respectively. The ratio m_(1)//m_(2) is close to -
View SolutionFigure. Shown a ring of mass M_(1) ans a sphere of mass M_(2) separated by a distance sqrt(3)R . A small object of mass m is displaced from A to B. Find the work done by gravitational forces.
View SolutionA thin fixed ring of radius 'R' and positive charge 'Q' is placed in a vertical plane. A particle of mass 'm' and negative charge 'q' is placed at the centre of ring. If the particle is given a small horizontal displacement, show that it executes SHM. Also find the time period of small oscillations of this particle, about the centre of ring. (Ignore gravity)
View SolutionA small ring of mass m is constrained to slide along a horizontal wire fixed between two rigid supports. The ring is connected to a particle of same mass by an ideal string & the whole system is released from rest as shown in the figure. If the coefficient of friction between ring A and wire is 35, the ring will start sliding when the connecting string will make an angle θ with the vertical, then θ will be (particle is free to move and ring can slide only)
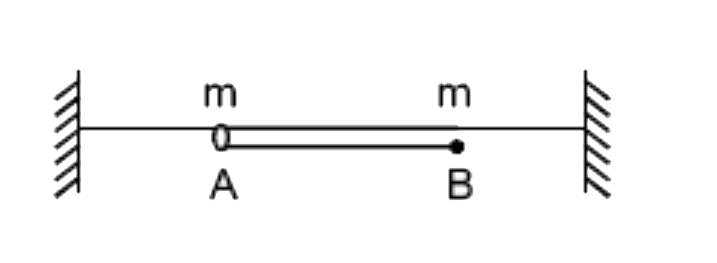
View SolutionA spherical bob of mass m and radius R is attached to a fixed point by means of a massless rigid rod whose length from the point of support up to the centre of bob is l. Find the period of small oscillation.
View Solution