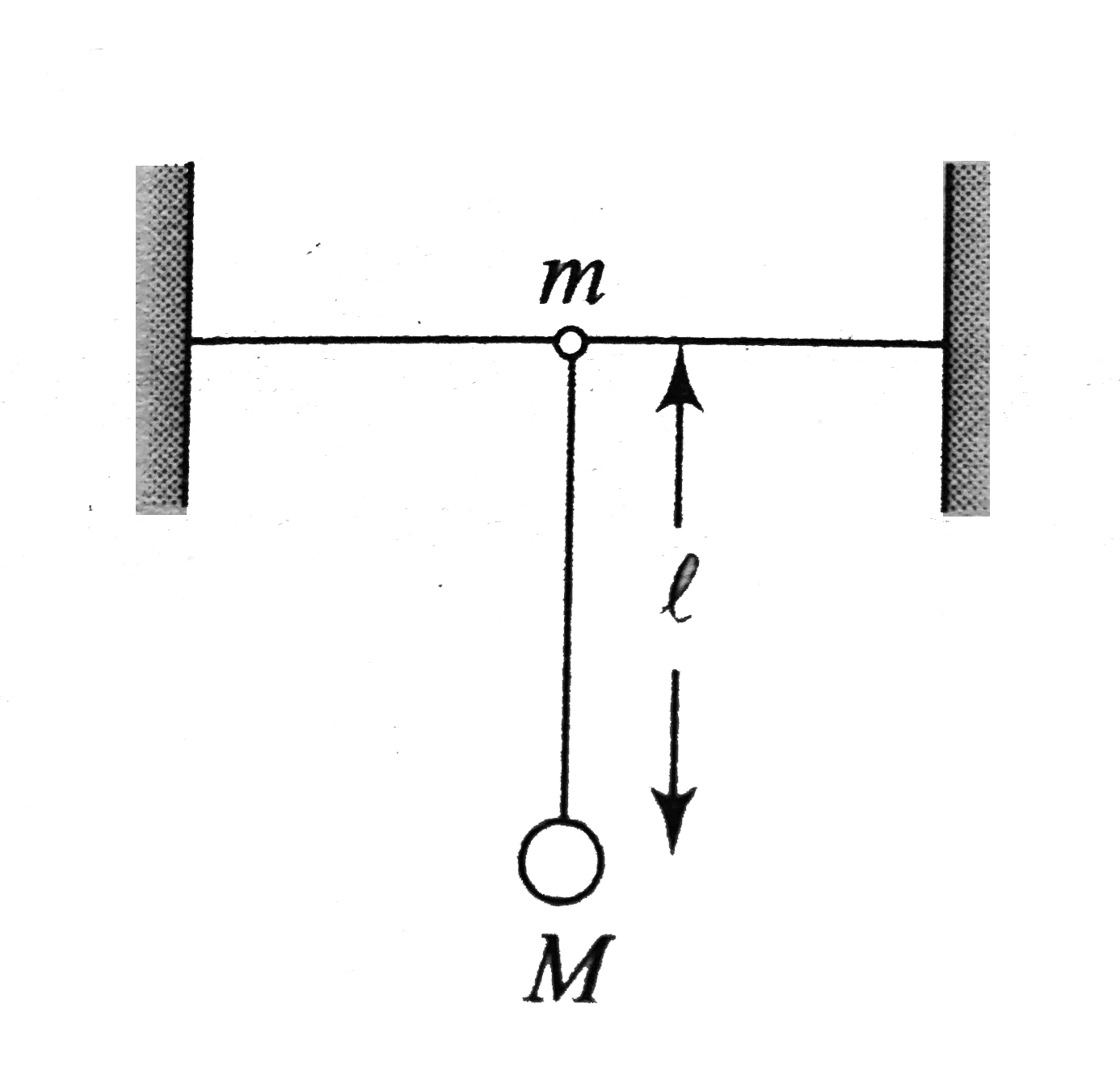
A smooth of mass m1 is lying on a rigid horizontal string A bob of mass m2 hangs from, the ring by an inextensible light string of length l. Find angular frequency of oscillation of the system.
The correct Answer is:√1+Mmgt
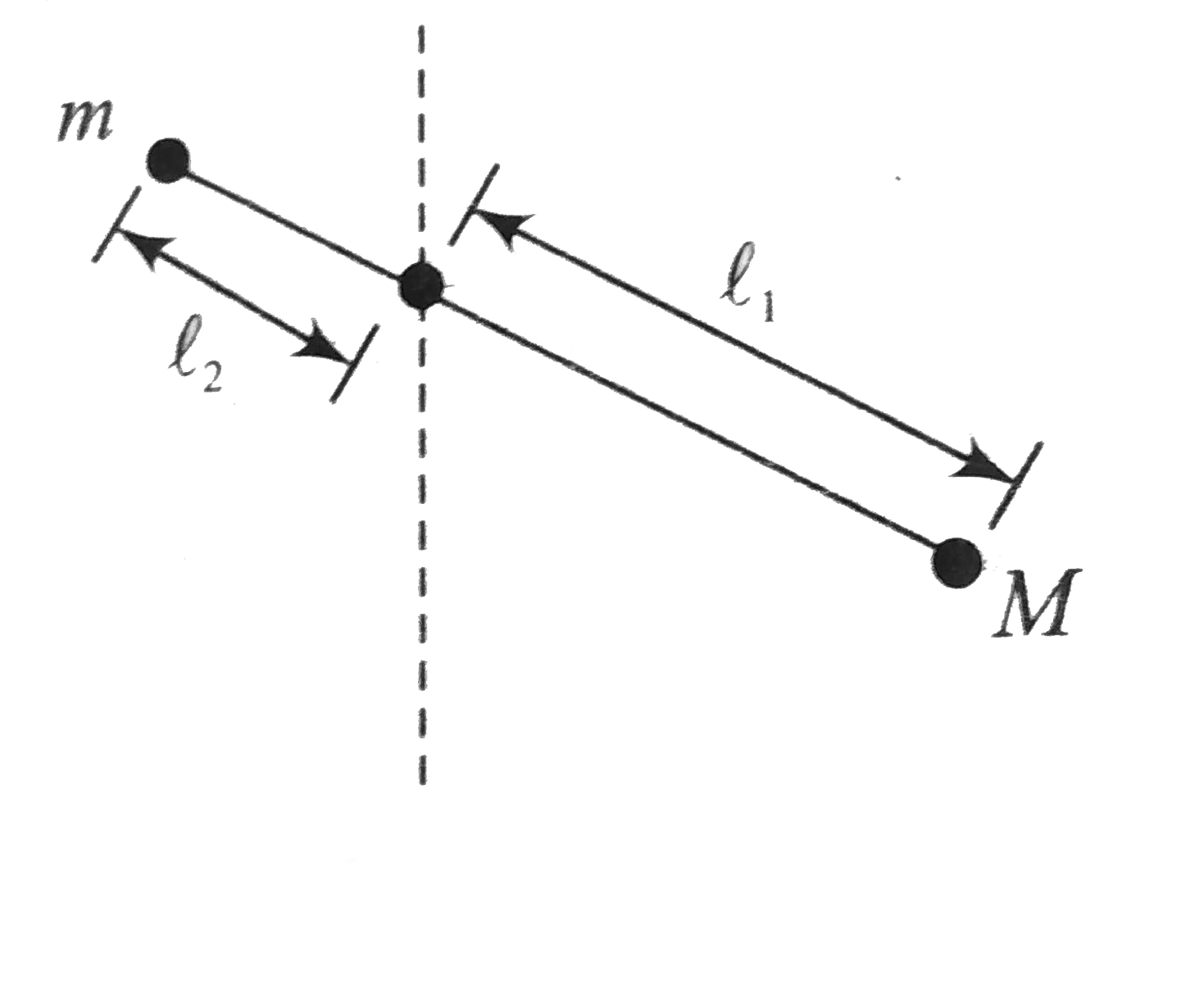
Both will oscillate about center of mass. The oscillation of M is same as a simple pendulum of mass M and length l1 . The time period both particles are . Let it is T.
T=2π√l1g
where l1 can be given as Ml2=ml2andl1+l2=l
l1=mlM+m
Then T=2π√ml(M+m)g
Topper's Solved these Questions
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Single Correct
107 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Multiple Correct
35 Videos
- LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - LINEAR AND ANGULAR SIMPLE HARMONIC MOTIONEXERCISE - Exercise 4.2
23 Videos
- KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - KINETIC THEORY OF GASES AND FIRST LAW OF THERMODYNAMICSEXERCISE - Interger
11 Videos
- MISCELLANEOUS KINEMATICSBOOK - CENGAGE PHYSICS ENGLISHCHAPTER - MISCELLANEOUS KINEMATICSEXERCISE - Interger type
3 Videos
Similar Questions
A loop of mass M with two identical rings of mass m at its top hangs from a ceiling by an inextensible string. If the rings gently pushed horizontally in opposite directions, find the angular distance covered by each ring when the tension in the string vanishes for once during their motion.

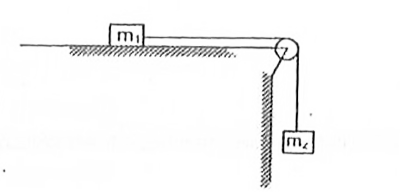
View SolutionA block of mass m1=2 kg is kept on a smooth horizontal table. Another block of mass m2=1 kg is connected to m1 by a light inextensible string passing over a smooth pulley as shown in the figure. If the blocks are released, what will be the (a) acceleration of each block (b) tension in the string?
View SolutionTwo blocks of masses m and M are connected by an inextensible light string . When a constant horizontal force acts on the block of mass M. The tension in the string is

View SolutionA block of mass m connected with a smooth prismatic wedge of mass M is released from rest when the spring is relaxed. Find the angular frequency of oscillation.

View SolutionA very light rod of length l pivoted at O is connected with two springs of stiffness k1 & k2 at a distance of a & l from the pivot respectively. A block of mass ma attached with the spring k2 is kept on a smooth horizontal surface. Find the angular frequency of small oscillation of the block m.
_S01_031_Q01.png)
View SolutionA block of mass m hangs by means of a string which goes over a pulley of mass m and moment of inertia l, as shown in the diagram. The string does not realtive to the pulley. Find the frequency of small oscillations.
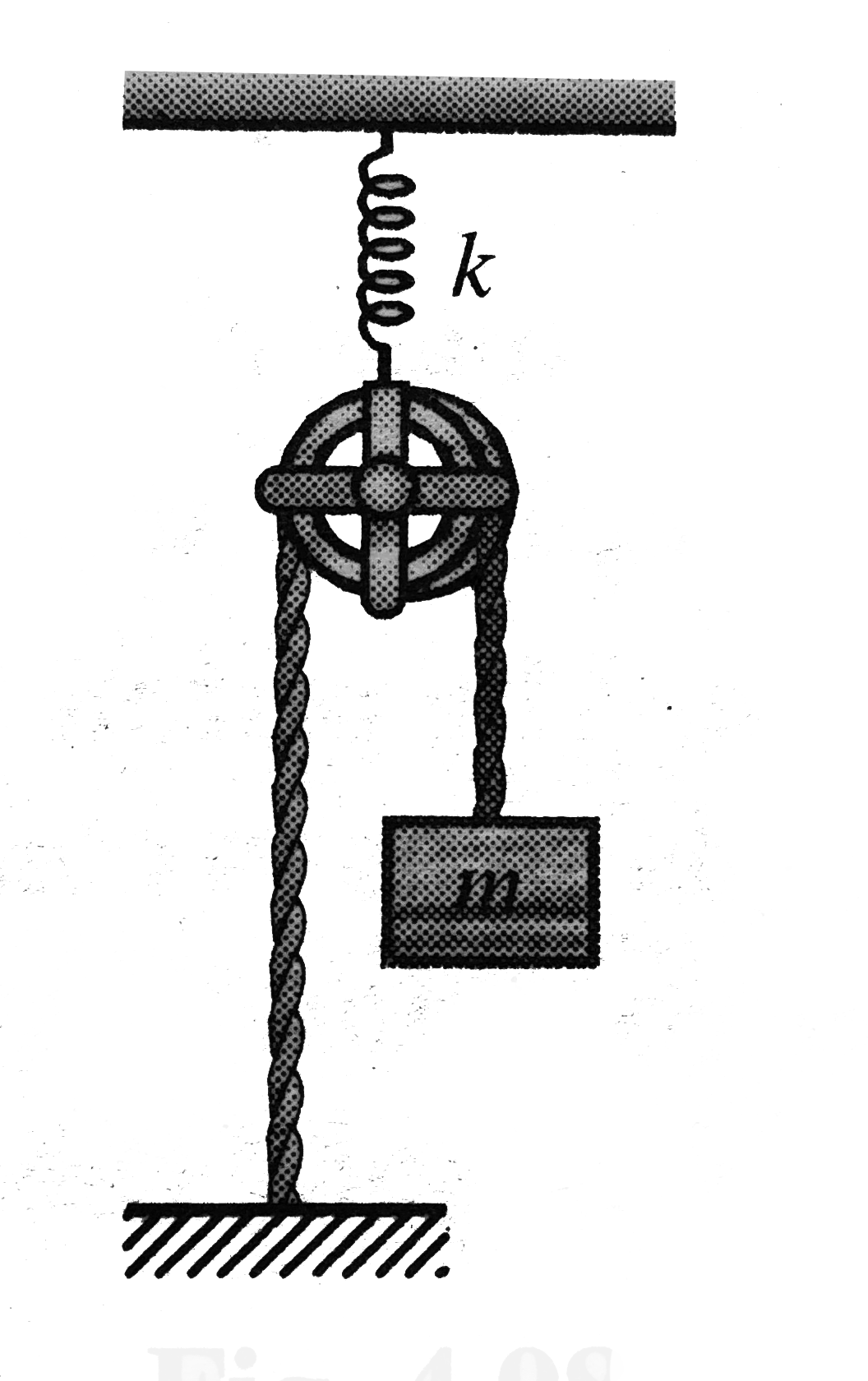
View SolutionA ring of mass m free to slide on a fixed smooth horizontal rod is attached to a particle of mass M kg by a inextensible string of length l. Initially, both M and m are at rest and the string is vertical. A horizontal velocity v0 is imparted to the particle. The maximum height up to which block will rise w.r.t its initial position is (M = 2m)
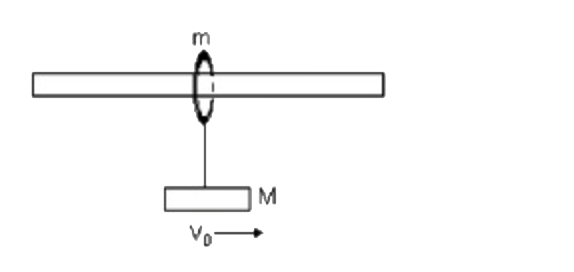
View SolutionA pendulum bob of mass 50 gm is hanging from the ceiling of a lift by a light , inextensible string. Choose the correct options ( g = 9.8 m/s2)

View SolutionA block of mass M is placed on a rough horizontal surface. It is connected by means of a light inextensible string passing over a smooth pulley . The other end of string passing over a smooth pulley. The other end of string is connected to a block of mass m. There is no friction between vertical surface and block m
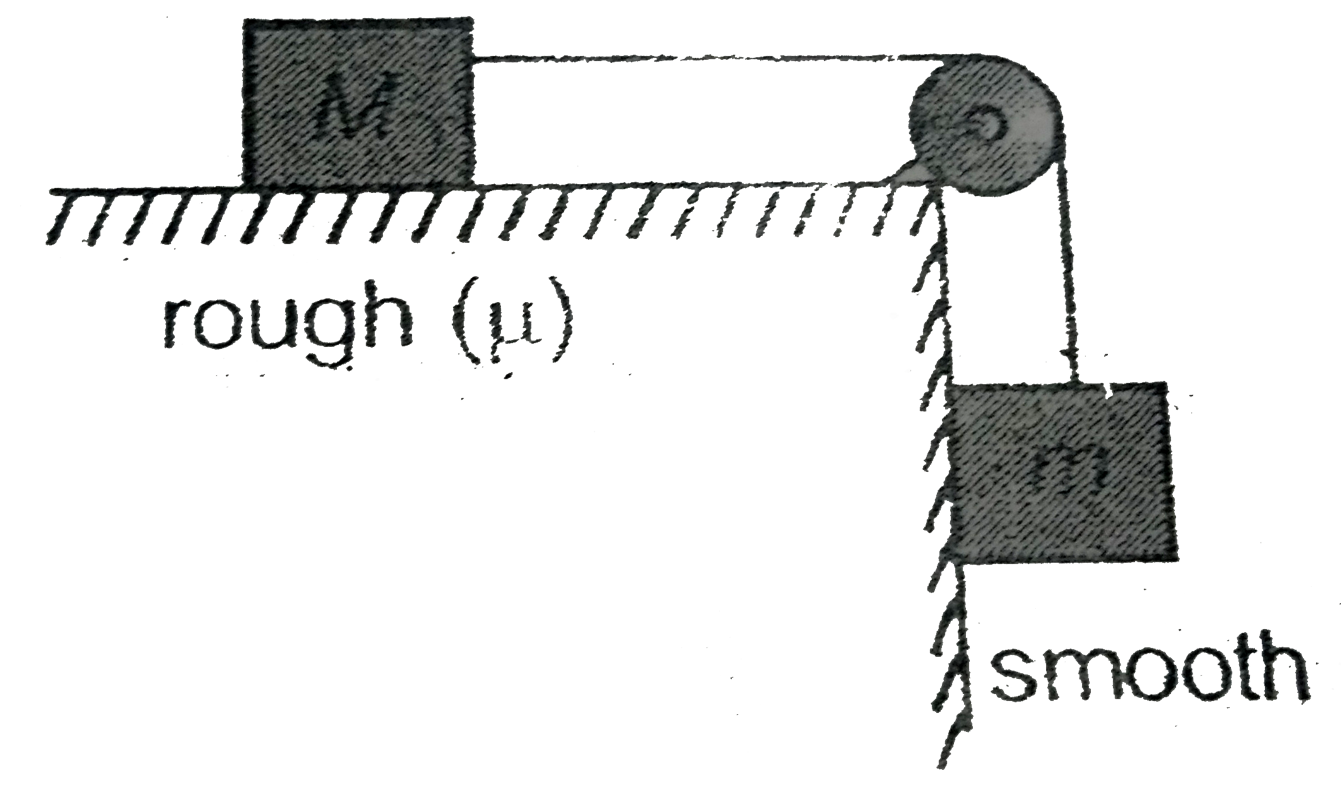
If the whole system ( horizontal surface + blocks ) accelerates towards right the value of maximum on the horizontal surface is
View SolutionTwo block of masses m1 and m2 are in equilibrium. The block m2 hangs from a fixed smooth pulley by an inextensible string that is fitted with a light spring of stiffness k as shown in fig. Neglecting friction and mass of the string, find the acceleration of the bodies just after the string S is cut.

View Solution
