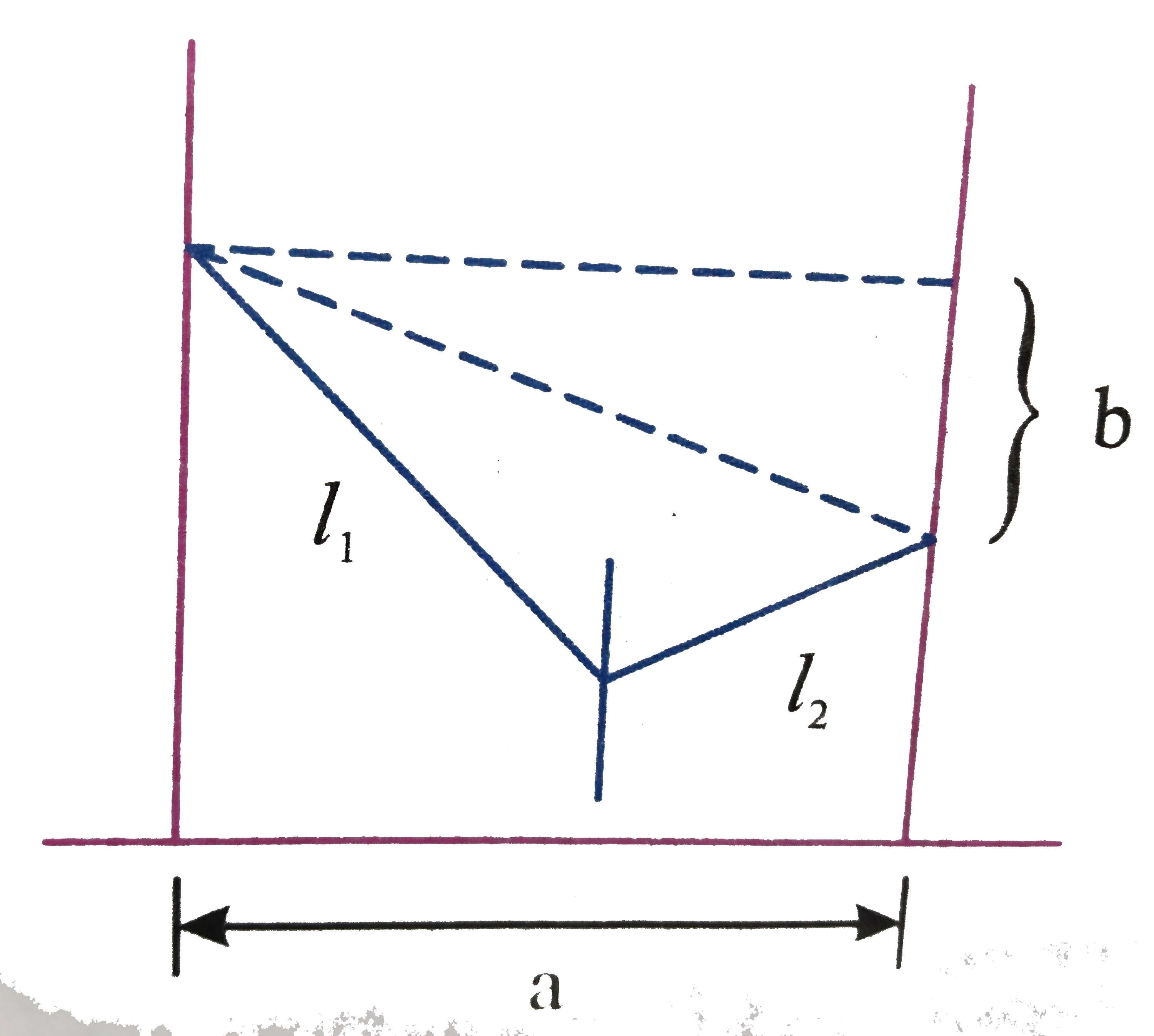
Consider a swing whose one end is fixed above the other rope by ''b'. The distance between the poles of swing is a. The lengths l1 and l2 are such that l21+l22=a2+b2 as shown. The period of the smaller oscillations of the swing, by neglecting the height of the swinging person, is.....
 Solution in Gujrati
Solution in Gujrati
The correct Answer is:A, B
Given a2+b2=l21+l22
tanθ=ba
tanα=l2l1
Let OT=x1,TQ=x1,PT=dTS=y
From geometry
d+y=l1sin(α+β)
and d+l1cos(α+θ)tanθ=l1sin(α+θ)
⇒d=l1l2a∴T=2π√dg=2π√l1l2ag
_E01_115_S01.png)
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]
39 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]
12 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]
20 Videos
- RACEBOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)
25 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
Similar Questions
If a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
View SolutionChoose the correct statement:
View SolutionIf L1&L2 are the lengths of the segments of any focal chord of the parabola y2=x, then (a) 1L1+1L2=2 (b) 1L1+1L2=12 (c) 1L1+1L2=4 (d) 1L1+1L2=14
View SolutionTwo rods of length l_(1) and l_(2) are made of material whose coefficient of linear expansion are alpha_(1) and alpha_(2) , respectively. The difference between their lengths will be independent of temperatiure if l_(1)//l_(2) is to
View SolutionOne rope of a swing is fixed above the other rope by b. The distance between the poles of the swing is a. The lengths l1 and l2 of the ropes are such that l21+l22=a2+b2 (Fig ).
Determine the period T of small oscillations of the swing, neglecting the height of the swinging person in comparison with the above lengths.

View SolutionIn the figure shown, there are two convex lenses L_(1) and L_(2) having focal. Lengths f_(1) and f_(2) respectively. The distance between L_(1) and L_(2) will be
View SolutionIf the lengths of the arms of a physical balance are l_(1) and l_(2) and a salesman weighs out twice to a customer articles of mass M by putting weughts first in one pan and then in the other, shown that the salesman is a loser by M[((l_(1)-l_(2))^(2))/(l_(1)l_(2))] .
View SolutionIf |x−a|<l1 and |x−b|<l2, show that |a−b|<l1+l2.
View SolutionIf l1 and l2 are the lengths of a seconds pendulum at the poles and the equator of the earth, then
View Solutionएक बच्चा झूले पर झूल रहा है । झूले की पृथ्वी तल से न्यूनतम व अधिकतम ऊँचाइयाँ क्रमशः 0.75 मीटर व, 2 मीटर है । झूले का अधिकतम वेग है -
View SolutionThe distance between two points P and Q is d and the lengths of projections of PQ on the coordinate planes are l1,l2,l3 then l1+l22+l23d2
View SolutionA simple pendulum of length L_(1) has a time period T_(1) and of length L_(2) has a time period of T_(2) then the time period of pendulum of length (L_(1)+L_(2)) is
View SolutionA simple pendulum of length L1 has a time period T2 then the time period of pendulum of length (L1+L2) is
View Solution
