A rod of mass M and length K is hinged at its one end n carris a block f mass m at its other end. A spring of force constant k1 is installed at distance a form the hinge and another of force constant k2 at a distance b as shown in the figure. If the whole arrangement rests on a smoth horizontal table top. Find the frequency of vibrations.
_E01_120_Q01.png)
Solution in Gujrati
The correct Answer is:A, B, C
_E01_120_S01.png)
For small angular displacement θ, net torque towards mean position is
τ=(k1aθ)a+(k2bθ)b⇒Iα=(k1a2+K2b2)θ
⇒(mL2+13ML2)α=(k1a2+k2b2)θ
⇒α=k1a2+k2b2L2(m+M3)θ∴ω2=k1a2+k2b2L2(m+M3)
Hence frequency
f=ω2π=12π
⎷k1a2−k2b2L2(m+M3)
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [B]12videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-04 [A]20videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
If a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
05:14View SolutionA particle of mass (m) is executing oscillations about the origin on the x axis. Its potential energy is V(x)=k|x|3 where k is a positive constant. If the amplitude of oscillation is a, then its time period (T) is.
02:35View SolutionA particle simple harmonic motion completes 1200 oscillations per minute and passes through the mean position with a velocity 3.14ms−1. Determine displacement of the particle from its mean position. Also obtain the displacement equation of the particle if its displacement be zero at the instant t=0.
08:05View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
04:16View SolutionChoose the correct statement:
00:35View SolutionTwo light springs of force constants (k_1 and k_2) and a block of mass (m) are in one line (AB) on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance (CD) between the free ends of the springs is (60 cms). If the block moves along (AB) with a velocity (120 cm//sec) in between the springs, calculate the period of oscillation of the block k1=1.8N/m,k2=3.2N/m,m=200gm).
(##JMA_CHMO_C10_026_Q01##).02:21View SolutionIn the figure a uniform rod of mass 'm' and length 'l' is hinged at one end and the other end is connected to a light vertical of spring constant 'k' as shown in figure. The spring has extension such that rod is equilibrium when it is horizontal . The rod rotate about horizontal axis passing through end 'B' . Neglecting friction at the hinge find (a) extension in the spring (b) the force on the rod due to hinge.
02:23View SolutionA rod of mass m and length l is hinged at 'its' end and released from rest in position shown. Find the force exerted by the hinge when the rod becomes horizontal
03:42View SolutionA rod of mass m and length l is hinged at one of its ends A as shown in figure. A force F is applied at a distance x from A . The acceleration of centre of mass varies with x as −
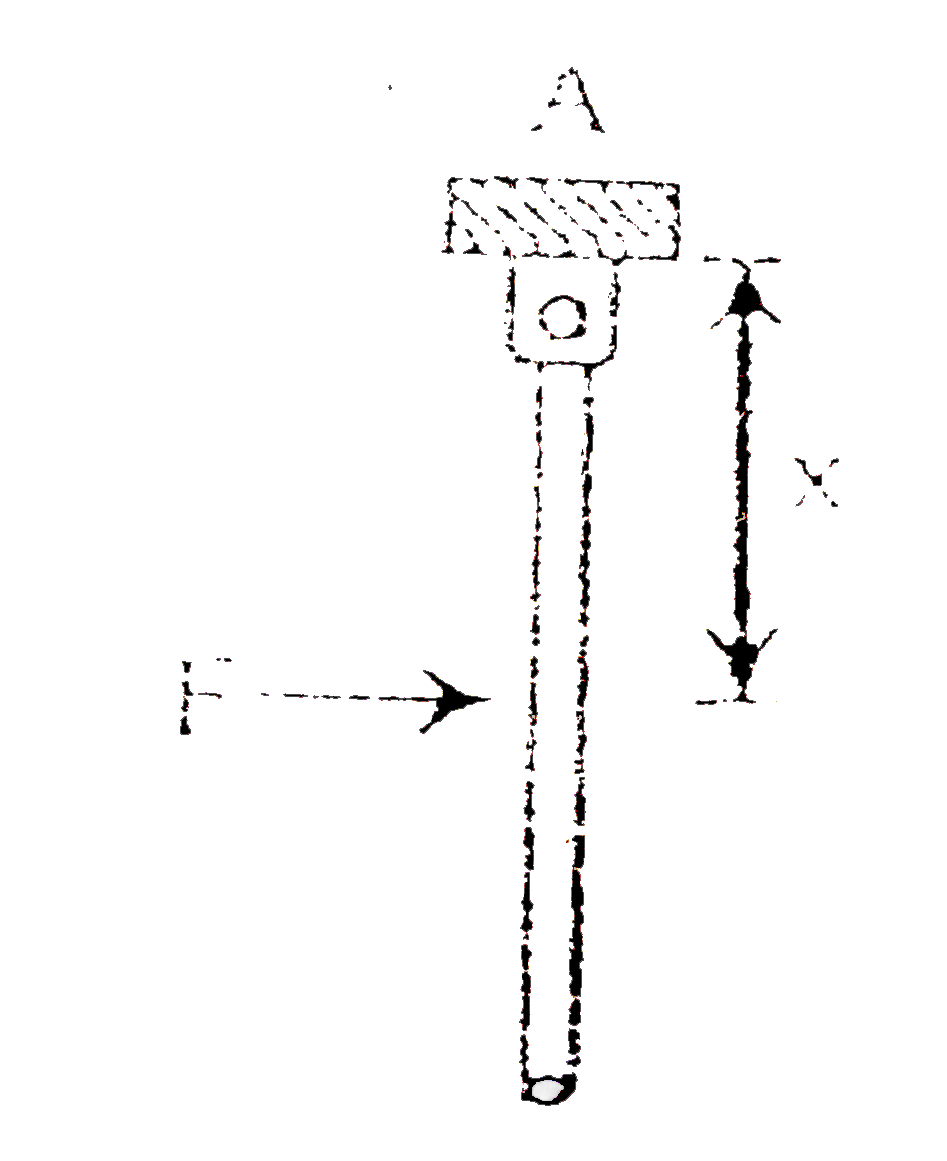
10:13View SolutionAs shown in the figure, two light springs of force constant k1 and k2 oscillate a block of mass m. Its effective force constant will be
05:17View SolutionA rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k_(1) is installed at distance a from the hinge and another of force constant k_(2) at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
04:10View SolutionA rod of mass M and length L is hinged at its one end and carries a particle of mass m at its lower end. A spring of force constant k_(1) is installed at distance a from the hinge and another of force constant k_(2) at B distance b as shown in the figure. If the whcich arrangement rests on a smoth horizontal table top, the frequency of vibration is :
01:19View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the
Horizontal component of the force applied by the hinge03:08View SolutionA uniform rod of mass 2m and length L is hinged at one end and carries a particle of mass m at the other end.Two springs each of force constant k are installed at distances as shown.The whole arrangement rests on a smooth horizontal surface.The frequency of small oscillations will be?
03:03View SolutionA rod of mass m and length L is hinged at its top end. If the rod is in equilibrium making an angle of 30∘ with the vertical when a horizontal force F is applied as shown in figure, then the value of F is:
04:20View SolutionTwo light spring of force constants k1 and k2 and a block of mass m are in one line AB on a smooth horizontal table such that one end of each spring is fixed on rigid supports and the other end is free as shown in the figure. The distance CD between the spring is 60cm. If the block moves along AB with a velocity 120cm/s in between the springs, calculate the period of oscillation of the block. (take k1=1.8N/m, k2=3.2N/m, m=200g)
06:23View Solution