A particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.Solution in Gujrati
at points away from the origin, the particle is in unstable equilibrium
for any finite non-zero value of x, there is a force directed away from the origin.
if its total mechanical energy is k2, It has its minimum kinetic energy away from the origin
from small displacements from x=0, the motion is simple harmonic.
The correct Answer is:D
U(x)=k(1−e−x2)
It is an exponential incresing graph of potential energy (U) with x2. Therefore U versus x graph will be as shown.
_E01_153_S01.png)
From the graph it is clear that at origin. Potential energy U is minimum (therefore, kinetic energy will be maximum) and force acting on the particle is also zero because
F=−dUdx=−(slope of U-x graph)=0
Therefore, origin is the stable equilibrium position. Hence, particle will oscillate simple harmonically about x=0 for small displacements. Therefore, correct option is (d). (a), (b) and (c) options are wrong due to following reasons :
(a) At equilibrium position F=−dUdx=0 i.e. shape of U−x graph should be zero from the graph we can see that slope is zero at x=0 and x=±∞.
Now among these equilibrium stable equilibrium position is that where U is minimum (Here x=0).
Unstable equilibrium position is that where U is maximum (Here none).
Netural equilibrium position is that where U is constant (Here x=±∞). Therefore, option (a) is wrong.
(b) For any finite non-zero value of x, force is directed towards the origin because origin is in stable equilibrium position. Therefore, option, (b) is incorrect.
(c) At origin, potential energy is minimum, hence kinetic energy will be maximum. Therefore, option (c) is also wrong.
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - MCQ s one or more than one correct answers5videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Paragraph3videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercise-05 [A]39videos
SIMPLE HARMONIC MOTION
- BOOK - ALLEN CHAPTER - RACEEXERCISE - Basic Maths (Wave Motion & Dopplers Effect) (Stationary waves & doppler effect, beats)25videos
RACE
- BOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS4videos
TEST PAPER
Similar Questions
Three simple harmonic motions in the same direction having the same amplitude and same period are superposed. If each differ in phase from the next by 45∘, then
04:12View SolutionA uniform thin cylindrical disk of mass M and radius R is attaached to two identical massless springs of spring constatn k which are fixed to the wall as shown in the figure. The springs are attached to the axle of the disk symmetrically on either side at a distance d from its centre. The axle is massless and both the springs and the axle are in horizontal plane. the unstretched length of each spring is L. The disk is initially at its equilibrium position with its centre of mass (CM) at a distance L from the wall. The disk rolls without slipping with velocity →V0=vacV0ˆi. The coefficinet of friction is μ.
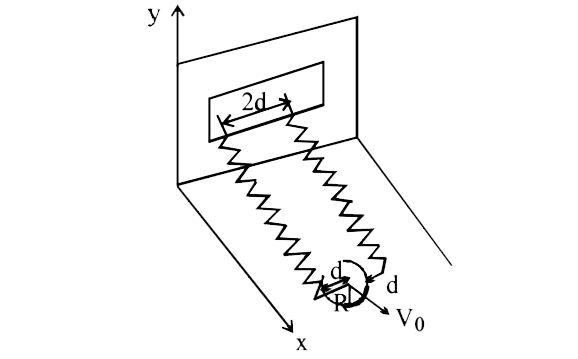
The net external force acting on the disk when its centre of mass is at displacement x with respect to its equilibrium position is.02:18View SolutionIf a spring has time period T, and is cut into (n) equal parts, then the time period of each part will be.
04:12View SolutionThe frequency of a radar is 780 MHz. After getting reflected from an approaching aeroplane, the apparent frequency is more than the actual frequency by 2.6 kHz. The aeroplane has a speed of
04:12View SolutionChoose the correct statement:
01:52View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)= k[1 - exp(-x^2)] for -o o le x le + o o , where (k) is a positive constant of appropriate dimensions. Then.
07:45View SolutionThe potential energy of a particle of mass m free to move along the x-axis is given by U=(1//2)kx^2 for xlt0 and U=0 for xge0 (x denotes the x-coordinate of the particle and k is a positive constant). If the total mechanical energy of the particle is E, then its speed at x=-sqrt(2E//k) is
01:44View SolutionA particle free to move along the X- axis has potential energy given by U(X)=k[1-exp(-X^(2))] of appropriate dimensions. Then-
05:52View SolutionA particle free to move along the x- axis has potential energy given by U(x) = k[1 - e^(-x^(2))] for -oo le x le + oo , where k is a positive constant of appropriate dimensions. Then select the incorrect option
05:00View SolutionThe area between the curve y=xsinx and x-axis where o≤x≤2π , is
04:44View Solutionx-अक्ष के अनुदिश गति करने के लिए स्वतन्त्र की स्थितिज ऊर्जा, सीमाओं −∞≤x≤+∞ के अंतर्गत, U(x)=k[1−e−x2] द्वारा दी जाती है,जहाँ k उपयुक्त विमाओं वाला धन नियतांक है। तब
यदि दो द्रव्यमान m1 तथा m2 स्प्रिंग की सहायता से जुड़े हैं तथा क्षैतिज सतह पर गति करने के लिए स्वतन्त्र हैं, तो आवर्तकाल
T=2π√μk
यहाँ, μ= समानित( Reduced) द्रव्यमान =m1m2m1+m202:42View SolutionA particle is placed at the origin and a force F = kx is acting on it (where k is a positive constant). If U (0) = 0, the graph of U(x) versus x will be (where U is the potential energy function)
02:01View SolutionA particle free to move along the x−axis has potential energy given by U(x)=k[1−e−x2] for −∞≤x≤+∞, where k is a positive constant of appropriate dimensions. Then select the incorrect option
02:26View SolutionA particle free to move along the (x - axis) hsd potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
01:47View SolutionA particle free to move along the (x - axis) has potential energy given by U(x)=k[1−exp(−x2)]for−oo≤x≤+oo, where (k) is a positive constant of appropriate dimensions. Then.
05:19View Solution